基于折线滑动面法的土石坝坝坡稳定分析

杨 才,丰土根

(1.河海大学岩土力学与堤坝工程教育部重点实验室,江苏南京210098;2.河海大学岩土工程研究所,江苏南京210098)

0 引 言

土石坝在外荷载及自重作用下,可能发生局部滑动。进行土石坝稳定分析的目地是保证坝体在自重、孔隙压力和外荷载的作用下,具有足够的稳定性,不致发生通过坝体或坝体连同地基的剪切破坏。对于非黏性土的坝坡,如心墙坝坝坡、斜墙坝的下游坝坡以及斜墙上游保护层连同斜墙一起滑动时,常形成折线滑动面[1]。本文以粘土心墙土石坝为算例,用折线滑动面法求出上、下游坝坡,在某一危险工况下的最小稳定安全系数或接近最小稳定安全系数Kc值,以论证选用坝坡的合理性,并归纳出相关结论。

1 折线滑动面稳定分析方法

假设滑动面只在坝壳中,而防渗体不连同坝壳一起滑动,属于非粘性土体滑动。对于部分浸水的非粘性土坝坡,水上和水下的物理性质不同,滑裂面近似折线面,所以采用折线滑动法,认为折点在水位附近。如图1所示。

图1 非粘性土坝上游坝坡稳定计算示意图

滑动面上的抗剪强度利用充分程度应该是一样的,其安全系数为:

图中B点为坐标原点,X轴水平指向上游,Y轴垂直指向地基,建立直角坐标系统。假设滑动面的三点A、D、C(按一定步长确定这三点的坐标),且滑动面不会切到心墙。其中A点在坝脚斜坡面上移动,但不会到达坝顶,D点为折坡点,C点实际是在防浪墙上游面坝体内部分移动,可以到达坝顶。

计算中把滑动土体 ADC(构成的滑动面)分成两个滑块,H点在上游水位延长线上,P1为相邻两土体滑面上的作用力,假定其方向平行于DC。将滑动土体分为DEBC及ADE两部分,各块重量分别为W1、W2,两块土体底面的抗剪强度指标分别为φ1、φ2,采用拟静力计算法,计算中所有力都可以简化到形心处,只考虑力的平衡,不考虑力矩的平衡。

DEBC块体的平衡式为:

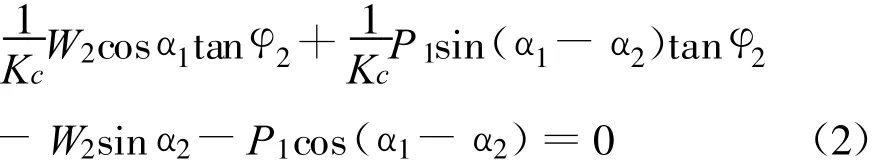
式中各符号的含义如图1所示。

考虑滑动面上抗剪强度发挥程度一样,两式中安全系数Kc应相等,故可联立方程求解Kc。根据工程等级,坝坡抗滑稳定的最小安全系数由规范查到。α1、α2可根据假定的 A点,C点,D点坐标求得,且要求 α1＞α2;每假定 A、C、D 点均有可能获得一个相应的Kc值,取其中最小值作为最终结果。采用VB程序编程[2]进行计算,可视化效果较好,操作简便[3]。

ADE块体的平衡式为:

2 工况选择及稳定分析成果

2.1 工况选择

稳定计算中需选取不利工况和不利部位进行稳定计算,本算例中对上下游坝坡分别计算以下几种工况的安全系数:

(1)水位在1/3坝高处;

(2)稳定渗流期设计洪水位;

(3)正常蓄水位+地震[4]。

2.2 算例工程参数

本算例工程拦河坝为粘土心墙土石坝,工程等级为Ⅱ级。库区正常蓄水位及下游水位分别为2 821.2 m和2 752.8 m,设计洪水位及下游水位分别为2 822.4 m和2 755.4 m,校核洪水位及下游水位分别为2 823.4 m和2 755.6 m,坝顶高程2 827.5 m,坝高77.5 m,上游坝坡坡率m1=2.5,下游坝坡坡率m2=2.0。上、下游坝坡土料参数见表1。

表1 上、下游坝坡土料参数

2.3 稳定计算成果

计算以上几种工况下的上、下游坝坡的最小稳定安全系数,计算成果见表2。

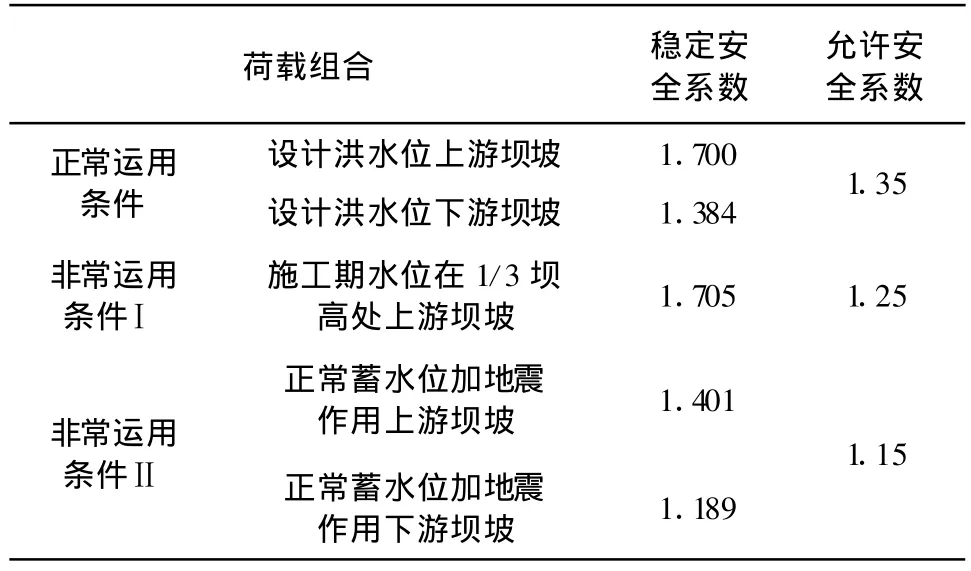
表2 各种工况上下游坝坡稳定计算成果表

3 稳定计算成果分析

3.1 坝坡稳定性分析

该工程主要建筑物土坝的等级为Ⅱ级,查规范可知其坝坡抗滑稳定的安全系数应满足以下条件:正常运用条件下不低于1.35,非常运用条件Ⅰ时不低于1.25,非常运用条件Ⅱ时不低于1.15[5]。由表2计算结果可见:在设计洪水位、1/3坝高水位及正常蓄水位加地震作用三种工况下,坝坡稳定性均能满足应用要求。其中正常蓄水位加地震作用工况对应稳定安全系数最小。

3.2 水位对上游坝坡稳定性的影响

当上游水位由正常蓄水位2 821.2 m降至死水位2 796 m的过程中,坝坡的稳定性也随之变化。由于计算中不考虑渗流力的作用,因此所得计算结果不准确,但可以反映坝坡稳定性的变化趋势[6]。

现取不同上游水位,进行稳定安全系数的计算。计算结果见表3。

表3 不同上游水位最小稳定安全系数

由表3可看出,随上游水位减小,上游坝坡的稳定安全系数Kc逐渐增大。反之,在蓄水期,随着上游水位的不断升高,坝体的稳定性逐渐减小。所以蓄水期是考验坝坡稳定性的关键时期[7]。

3.3 折坡折点对上游坝坡稳定的影响

对于坝坡稳定安全系数的计算,利用所编制的程序,绘出折面,通过控制变量法,固定D点纵坐标,改变D点的横坐标,分别计算稳定安全系数Kc值。

本次计算以上游坝坡,设计洪水位工况为例,在设计洪水位2 822.4m时,由程序可计算得滑动块体最低角点坐标为 A(70.25,28.1),折点处坐标为D(8.1,5)上折坡水平角 α1为31.69°,下折坡水平角α2为20.39°,最小稳定安全系数为1.700。

现控制A点坐标为(70.25,28.1),C点与B点重合,改变D点坐标分别计算稳定安全系数,计算结果见表4。

表4 不同折点D稳定安全系数

根据表4中计算所得结果,以Dx为横坐标,Kc为纵坐标绘制图2,可更直观的看出Kc值随折坡点位置变化的规律,并根据曲线形状得出结论。

随着Dx的增大,稳定安全系数变化趋势为先逐步减小,当Dx为8.1 m时达到最小值为1.700,随后又逐步增大,下折线越来越缓,上折线越来越陡,在整个折坡中曲线成抛物线分布,稳定安全系数均在允许范围内。

文献[8]中得出的结论:坝内最小Kmin值的折面不会通过坝顶平面,只限于坝坡范围内。与本文中计算得出的结论是一致的,并且本文通过计算得出了最小安全系数Kc随折点在坝体深入程度的变化规律,在具体工程中通过控制滑坡面增大安全系数具有实践意义。

4 结 语

(1)坝坡稳定性计算[9]是大坝设计的重要环节,可以采用的方法很多,比如滑动面法,应力应变分析法或实验分析法等[10]。本文采用折线滑动面法。无粘性土土坡的失稳滑动往往呈坡面表层滑动,上游坝坡部分浸水,危险滑动面可能会向坝体内深入。

(2)将滑动面限制在坝坡中,采用折线滑动法进行计算,考虑的荷载主要有:自重,地震荷载。计算中假定坝壳料均匀,各部分物理力学性质相同,采用总应力法分析。由于坝壳料的渗透系数较大,不考虑渗流力。

(3)通过稳定计算程序分析,得到水位在1/3坝高处、稳定渗流期设计洪水位、正常蓄水位加地震作用三种工况下坝坡稳定安全系数,并可以相对直观的观察滑动面的位置。此外,讨论了水位的变化以及滑动面折点位置变化对坝坡稳定性的影响。

[1] 林益才.水工建筑物[M].北京:中国水利水电出版社,1997.

[2] 苟平章,任小康.Visual Basic程序设计[M].北京:科学出版社,2008.

[3] 吴余生,陈胜宏.边坡稳定极限平衡分析软件研究[J].水力发电学报,2005,24(6):35-39.

[4] 中国水电水利科学研究院.DL 5073-2000.水工建筑物抗震设计规范[S].北京:中国电力出版社,2001:25-27.

[5] 中国水电工程顾问集团西北勘测设计研究院.DL/T 5395-2007.碾压式土石坝设计规范[S].北京:中国电力出版社,2007:50-51.

[6] 安 民,张世勤,陈国平.库水位升降对某均质土坝坝坡稳定影响分析[J].中国农村水利水电,2008,(11):87-89.

[7] 张 玉,张方方.变水位多工况下大型渠道土质边坡的稳定分析[J].水利水电科技进展,2010,30(1):56-60.

[8] 王鸿兴.无粘性土坝坡稳定分析[J].岩土工程学报,1885,7(3):47-57.

[9] 罗国武,区军雄.土石坝坝坡失稳模糊风险分析[J].水利与建筑工程学报,2012,10(1):173-176.

[10] 吕擎峰.土坡稳定分析方法研究[D].南京:河海大学,2005:20.