标准Ⅰ型马蹄形断面水力特性的研究

张志昌，李若冰

（西安理工大学水利水电学院，西安 710048）

标准Ⅰ型马蹄形断面水力特性的研究

张志昌，李若冰

（西安理工大学水利水电学院，西安 710048）

为研究标准Ⅰ型马蹄形断面正常水深、弗劳德数和收缩断面水深的计算方法，根据明渠均匀流理论、明渠恒定非均匀流理论和能量方程，分析了标准Ⅰ型马蹄形断面的水力特性，提出了3种工况下的正常水深与流量关系、弗劳德数，以及2种工况下收缩断面水深的迭代计算公式，并通过算例给出了解题过程。研究成果计算简单、精度高，可以应用于实际工程。

标准Ⅰ型马蹄形断面;正常水深;弗劳德数;收缩断面水深

1 研究背景

标准Ⅰ型马蹄形断面是由底部的弓形、下部两侧的扇形以及顶拱半圆形组成的［1］，其中底部弓形和两侧扇形的半径均为3r，圆心角α为常数，顶拱半圆的半径为r。由于断面形状比较复杂，文献［2］在计算标准Ⅰ型马蹄形断面正常水深流量关系时没有给出具体计算公式，而是给出了表格以供查询。近几年来，随着计算机的发展，迭代计算已变得非常简单，有些学者对标准Ⅰ型、Ⅱ型马蹄形断面的水力特性进行了研究。文献［3-5］研究了标准Ⅱ型马蹄形断面正常水深与流量的关系;文献［6］研究了标准Ⅱ型马蹄形断面均匀流水深的简化计算方法;文献［7］对标准Ⅰ型和Ⅱ型断面的正常水深流量关系给出了迭代计算公式，但未给出详细的公式推导过程;文献［8］引入准一次函数和准二次函数的概念，将马蹄形断面分为3种情况，给出了正常水深的近似计算公式，该公式形式比较简洁，在工程常用范围内误差小于0.31%;文献［9］引入变量t，通过逐次逼近及优化拟合，给出了标准Ⅰ型和Ⅱ型马蹄形断面的正常水深的计算方法，其优点是将2种断面形式的公式合并为1种公式，公式误差小于0.5%。对于标准Ⅰ型马蹄形断面的弗劳德数和收缩水深，目前尚未看到研究成果。

本文从明渠均匀流的基本公式出发，研究了3种工况下标准Ⅰ型马蹄形断面正常水深的迭代公式;同时还研究了标准Ⅰ型马蹄形断面的弗劳德数以及收缩断面水深的计算方法，通过实例给出了计算过程，为工程设计提供了方便。

2 标准Ⅰ型马蹄形断面的基本形式和圆心角

标准Ⅰ型马蹄形断面见图1，它由底部弓形、下部扇形和顶拱的半圆形断面组成。

图1 标准Ⅰ型马蹄形断面Fig.1StandardⅠ-type horseshoe cross section

顶拱半圆的半径为r，下部三圆弧段的半径均为3r，底部弓形断面的圆心角为2α，侧面扇形圆心角为α。由图可见

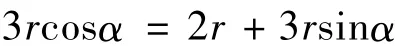
由上式可以解出α=16.874 49°，可以看出标准Ⅰ型马蹄形断面的圆心角为常数。

3 标准Ⅰ型马蹄形断面的正常水深

一般渠道的正常水深流量关系为［10］式中:Q为流量;C为谢才系数;R为水力半径;χ为湿周;i为渠道的底坡;n为糙率;A为过水断面面积。

标准Ⅰ型马蹄形断面的水深如图2所示，可能有3种情况:①水深处于底部弓形断面内，如图2（a）所示;②水深处于下部扇形断面内，如图2（b）所示;③水深处于顶拱半圆形断面内，如图2（c）所示，现对这3种情况讨论如下。

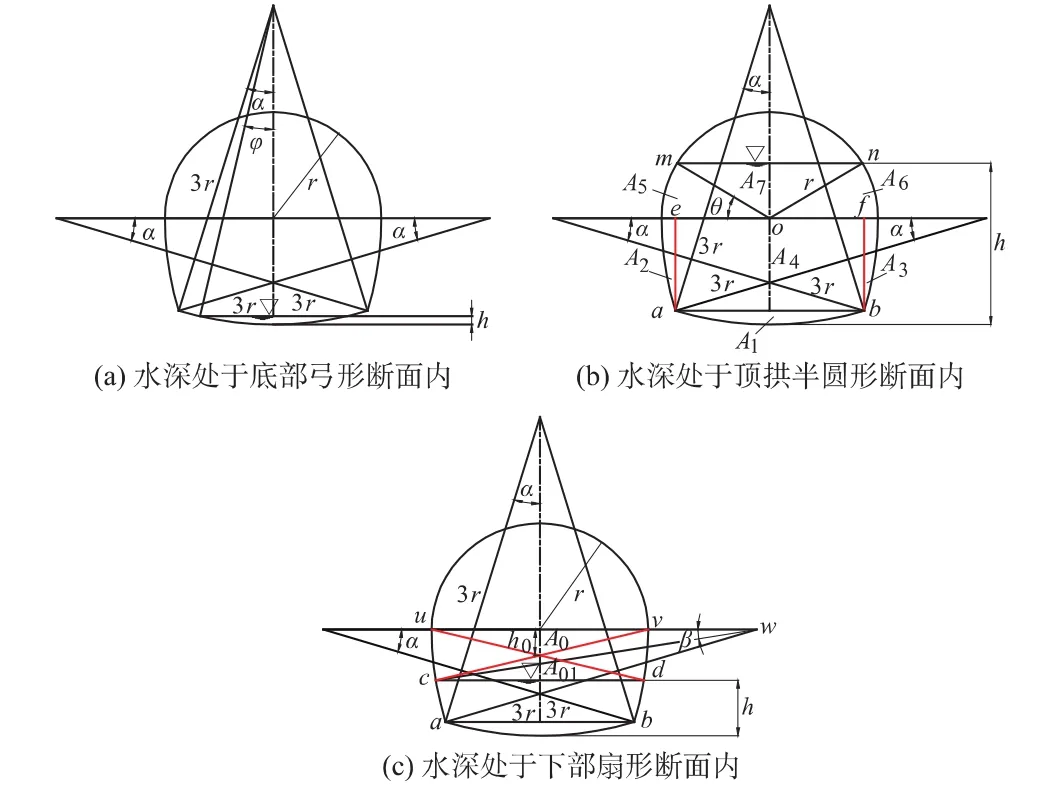
图2 标准Ⅰ型马蹄形断面的水深分类Fig.2Classification for the water depth of standardⅠ-type horseshoe cross section

3.1 水深处于底部弓形断面

如图2（a）所示，此时断面面积、湿周和水深的计算公式分别为

式中:r为顶拱半圆的半径;φ为水深为h时的半圆心角;h为水深。

正常水深-流量关系为

3.2 水深处于顶拱半圆形断面

由图2（b）可以看出，过水断面面积由7部分组成，弓形断面面积A1=9r2（α-sinαcosα），扇形断面内的面积可以分为两侧的半弓形面积A2，A3和中间的矩形面积A4，其中A2=A3，A1=A2+A3。由图中

3.3 水深处于下部扇形断面

由图2（c）可以看出，下部水深淹没面积为

正常水深-流量关系为

其中β的取值范围为0°～24.295 19°，如果水深已知，则可由（15）式求出β，代入（14）式即可计算出流量。如果已知流量求水深，可以将（14）式写成迭代公式为

例题1:现以文献［2］为例，验证某马蹄形标准Ⅰ型断面。已知顶拱半径r=1.5 m，渠道底坡i= 1/2 000，糙率n=0.014，试计算正常水深与流量的关系。

解:

底部弓形断面高度为

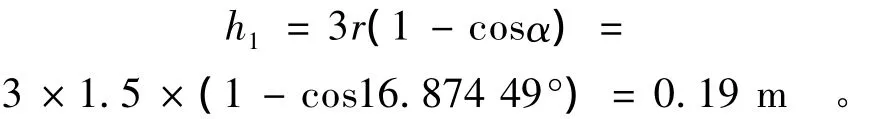
计算时应注意:顶拱上要留出一定的余幅，根据文献［1］，对于低流速的无压隧洞，在通气良好的情况下，净空断面积一般不得小于隧洞断面面积的15%，净空高度不小于40 cm。本例题中隧洞高度为3.0 m，设水深分别为0.15，0.19，0.30，0.60，0.90，1.20，1.50，1.80，2.10，2.40 m，计算时，当水深h≤h1时，用公式（5）计算流量;当水深h1＜h≤r时，用公式（14）计算流量;当水深h＞r时，用公式（9）计算流量。计算结果见表1。

表1 正常水深－流量关系计算表Table 1Calculation results of the relation between normal water depth and flow

4 标准Ⅰ型马蹄形断面的弗劳德数

弗劳德数的计算公式［11］为

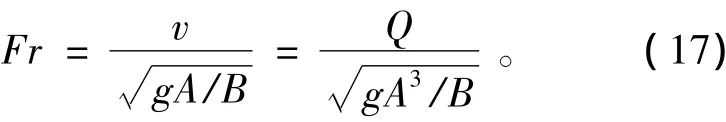
式中:B为水面宽度;g为重力加速度。

标准Ⅰ型马蹄形断面的弗劳德数分为3种情况:

（1）水深处于底部弓形断面内

5 标准Ⅰ型马蹄形断面收缩断面水深的计算

从溢流坝下泄的水流在坝址处水深最小，此处称为收缩断面，相应的水深为收缩断面水深（见图3）。收缩断面水深是计算溢流坝消能、临界水跃的重要参数，收缩断面底部以上总水头E0一般是已知的，由能量方程得

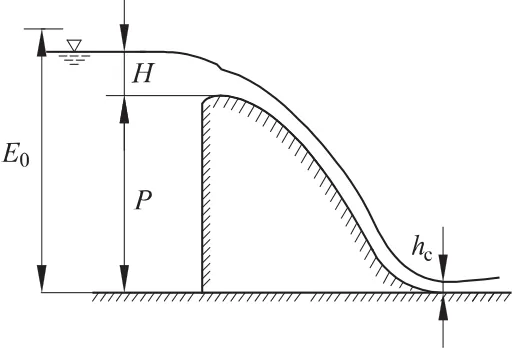
图3 收缩断面水深示意图Fig.3Sketch of contracted section’s water depth

式中:ø为流速系数，其确定方法可查阅文献［12］;Ac为收缩断面面积;hc为收缩断面水深，因为该水深为渠道的最小水深，一般位于马蹄形断面的底部弓形断面内或下部的扇形断面内。

当水深位于底部弓形断面内时，断面面积Ac、收缩断面水深hc分别用式（2）和式（4）计算，将Ac，hc代入（21）式可得迭代公式为

由上式迭代求出φ后，由下式即可求得收缩断面水深hc为

当水深位于下部扇形断面内时，断面面积Ac、收缩断面水深hc分别用式（12）和式（15）计算。将Ac，hc代入式（21）可得迭代公式为

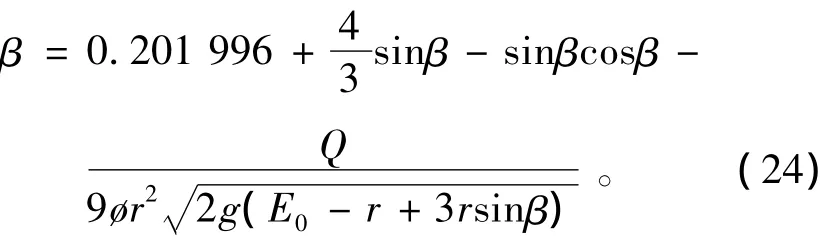
由上式迭代求出β后，由下式即可求得收缩断面水深hc为

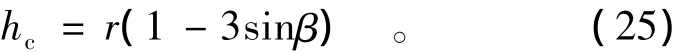
例题2:某溢流坝从坝址算起的上游总水头为80 m，下游渠道采用标准Ⅰ型马蹄形断面，已知顶拱半径r=5 m，渠道通过的流量Q=290 m3/s，流速系数ø为0.9，试求坝址处的收缩断面水深。

解:

底部弓形断面高度为

假定收缩断面水深处于下部扇形断面内，用公式（24）计算夹角β，将有关参数代入得

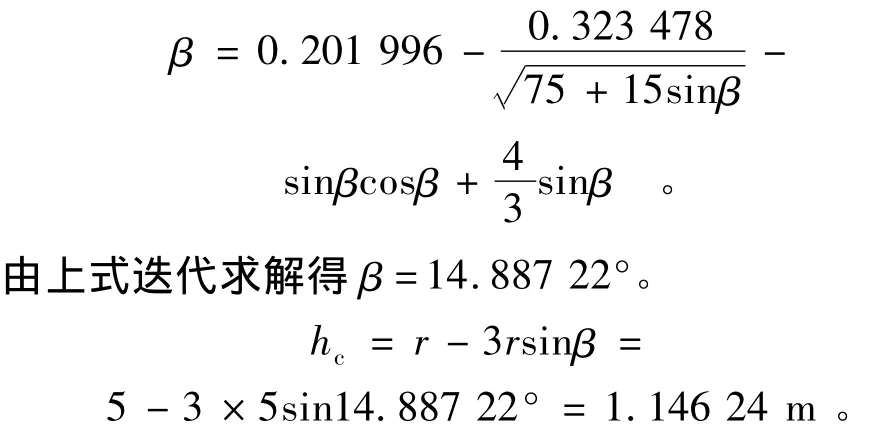
因为h1＜hc＜r，所以假定收缩断面水深位于下部扇形断面内是正确的。

6 结语

本文综述了马蹄型断面正常水深的研究成果，推导了标准Ⅰ型马蹄形断面正常水深、弗劳德数，以及收缩断面水深的计算方法。公式推导过程详细明确，与目前已有的研究成果比较，公式计算简单、迭代方便、精度高，并通过实例给出了计算步骤，可为教学和工程设计提供参考。

［1］林继镛.水工建筑物（第四版）［M］.北京:中国水利水电出版社，2007:402-412.（LIN Ji-yong.Hydraulic Structure（The Fourth Edition）［M］.Beijing:China Water Power Press，2007:402-412.（in Chinese））

［2］武汉水利电力学院水力学教研室.水力计算手册［M］.北京:水利电力出版社，1983:390-409.（Teaching and Researching Office of Hydraulics in Wuhan University of Hydraulic and Electrical Engineering.Handbook of Hydraulic Calculation［M］.Beijing:Water Resources and Electric Power Press，1983:390-409.（in Chinese））

［3］李永刚.马蹄形隧洞水力计算迭代法［J］.人民黄河，1955，（11）:42-44.（LI Yong-gang.Iterative Method of Hydraulic Calculation on Horseshoe Section Tunnel［J］. Yellow River，1955，（11）:42-44.（in Chinese））

［4］谭新莉.马蹄形断面水力学计算［J］.新疆水利，2003，（2）:20-23.（TAN Xin-li.Hydraulic Calculation on Horseshoe Shaped Section［J］.Xinjiang Water Resources，2003，（2）:20-23.（in Chinese））

［5］张润生，刘学文，彭月琴.马蹄形断面隧洞各水力要素的求解［J］.山西水利科技，1994，（4）:44-47. （ZHANG Run-sheng，LIU Xue-wen，PENG Yue-qin. Solution of Hydraulic Element of Horseshoe Section Tunnel［J］.Shanxi Hydrotechnics，1994，（4）:44-47.（in Chinese））

［6］腾凯，刘继忠，李松岩，等.马蹄形过水断面均匀流水深的简化计算法［J］.人民黄河，1997，（1）:36-38. （TENG Kai，LIU Ji-zhong，LI Song-yan，et al.Simplified Calculation Method of Uniform Flow Depth of the Horseshoe Cross Section［J］.Yellow River，1997，（1）: 36-38.（in Chinese））

［7］吕宏兴，辛全才，花立峰.马蹄形过水断面正常水深的迭代计算［J］.长江科学院院报，2001，18（3）:7-10. （LV Hong-xing，XIN Quan-cai，HUA Li-feng.Calculation on Normal Depth of Horseshoe Cross Section by Iterative Method［J］.Journal of Yangtze River Scientific Research Institute，2001，18（3）:7-10.（in Chinese））

［8］赵延风，王正中，芦琴.马蹄形断面正常水深的直接计算公式［J］.水力发电学报，2012，31（1）:173-177. （ZHAO Yan-feng，WANG Zheng-zhong，LU Qin.Direct Calculation Formulas for Normal Depth of Horseshoe Section［J］.Journal of Hydroelectric engineering，2012，31 （1）:173-177.（in Chinese））

［9］LIU Ji-liang，WANG Zheng-zhong，FANG Xing，et al. Iterative Formulas and Estimation Formulas for Computing Normal Depth of Horseshoe Cross-Section Tunnel［J］. Journal of Irrigation and Drainage Engineering，2010，136（11）:786-790.

［10］张志昌.水力学（下册）［M］.北京:中国水利水电出版社，2011:69-90.（ZHANG Zhi-chang.Hydraulics （The Second Volume）［M］.Beijing:China Water Power Press，2011:69-90.（in Chinese））

［11］清华大学.水力学（修订本）上册［M］.北京:高等教育出版社，1980.（Tsinghua University.Hydraulics（Revised Edition）［M］.Beijing:Higher Education Press，1980.（in Chinese））

［12］李建中，宁利中.高速水力学［M］.西安:西北工业大学出版社，1994:196-201.（LI Jian-zhong，NING Lizhong.High Speed Hydraulics［M］.Xi’an:Northwestern Polytechnic University Press，1994:196-201.（in Chinese ））

（编辑:刘运飞）

Hydraulic Characteristics of StandardⅠ-Type Horseshoe Cross Section

ZHANG Zhi-chang，LI Ruo-bing
（Institute of Water Resources and Hydro-electric Engineering，Xi’an University of Technology，Xi’an710048，China）

The present study aims to research the calculation method of normal water depth，Froude number and contracted section’s water depth in standardⅠ-type horseshoe cross section.On the basis of the theories of uniform flow and non-uniform flow in open channel and the energy equation，the hydraulic characteristics of standardⅠ-type horseshoe cross section are analyzed.Iterative calculation formulas of the relationship between normal water depth and flow，Froude number under three conditions and water depth of contracted section under two conditions are put forward.The calculating process is illustrated by examples.The calculation method is simple and convenient with high precision，hence can be applied to engineering practice.

standardⅠ-type horseshoe cross section;normal water depth;Froude number;water depth of contracted section

TV133.1

A

1001-5485（2013）05-0055-05

10.3969/j.issn.1001-5485.2013.05.013

2013，30（05）:55-59

2012-02-27;

2012-03-17

张志昌（1954-），男，陕西西安人，教授级高级工程师，主要从事水工水力学方面的研究，（电话）13991942265（电子信箱）zhangzhichang1954@163.com。

李若冰（1988-），女，河南禹州人，硕士研究生，从事水工水力学方面的研究，（电话）13679175031（电子信箱）liruobing513@163. com。