常系数线性微分方程组的基解矩阵的一种新求法

彭庆英

（常州技师学院，江苏常州 213000）

1 引 言

对于常系数线性微分方程组

其中A为n×n常数方阵，x＝x（t）是未知的n维列向量.关于方程组（1）的求解问题，总是个繁杂的问题，而求解的关键在于求其一个基解矩阵.根据A的特征向量的特点采取合适的方法尤为重要，合适的方法可以使计算简捷.不同体系的教材，都大致相同地介绍了多种不同的求解方法.然而，不管矩阵A有没有n个线性无关的特征向量，利用哈密顿—凯莱定理求基解矩阵都是一种行之有效的方法.因此，文章对该方法计算基解矩阵expAt进一步研究.

2 利用哈密顿—凯莱定理计算基解矩阵

的解.

定理2将计算基解矩阵expAt的问题归结为求解齐线性微分方程组（3）满足初始条件（4）的初值问题.由于方程组（3）是一个特殊的一阶常系数齐次线性方程组，其系数矩阵

是一个下三角矩阵，容易直接求解且其解可用初等函数的有限积分形式来表达，并且当A为实矩阵时，由公式（2）求出来的基解矩阵一定是实的.该方法是通过解微分方程求基解矩阵.但事实上，有时候解微分方程组也是比较麻烦的.通过改进将解微分方程组转化为解线性方程组的问题.进而得到一种求解基解矩阵的简单易行的方法.

定理3 对于方程组（1），设n阶方阵A的各相异特征根为λj（j＝1，2，…，s），其对应的重数为mj，则方程组（1）的标准基解矩阵

例1中解法1是利用定理2通过解微分方程组来解决，解法2是利用定理3解决的，定理3将计算基解矩阵expAt的问题归结为求解关于a0（t），a1（t），…，an－1（t）的非齐次线性方程组（6）的问题，而解方程组（6）可利用线性代数中的方法，如对系数矩阵进行初等行变换，方法更简单.

3 应 用

从常微分方程诞生之日起，就根植在生产和生活实际中，并且伴随着物理和其他工程学（如生物工程、信息工程、环境工程甚至人口与计划工程）的发展而不断丰富和发展.下面我们给出一个实际应用的例子，并利用前面所讲的方法求解.

3.1 复杂电路的计算

在由电阻、电感和电源等组成的多回路的复杂电路中，可以通过回路电压定律和节点电流定律建立起描述各支路中电流所满足的方程组.通过求解而得到电流的变化规律.考虑图1所示的复杂电路中电流的变化规律.

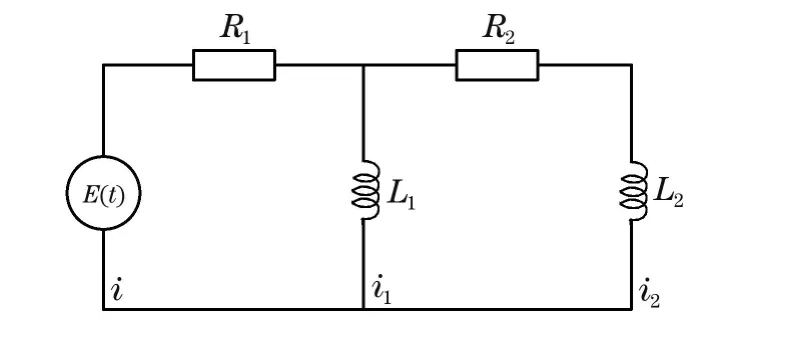
图1

［1］北京大学数学系几何与代数教研室代数小组.高等代数［M］.2版.北京：高等教育出版社，1988：303.

［2］周义仓，靳祯，秦军林.常微分方程及其应用［M］.2版.北京：科学出版社，2010：195－196.

［3］王高雄.常微分方程［M］.2版.北京：高等教育出版社，1996：236，209.