关于分配格的判定问题

郭 芸， 王朝晖

（苏州大学计算机科学与技术学院，江苏苏州 215006）

分配格的判定是离散数学课程中的一个基本问题，它要求学生在对基本概念有深入理解的同时，又具备一定的计算能力，这就导致学生在处理该类问题时经常会犯错，甚至离散数学教材的配套习题解答书在该问题上也出错.探索如何有效解决这一教学问题显得很有必要.在思考过程中我们想到，由于离散数学的教学对象主要是计算机学院的学生，既然他们已经具备一定的计算机运用能力，那为何不因地制宜结合计算机这一工具呢？事实证明我们这个想法在教学实践中取得了较好的效果.下面本文通过一个具体的例子来对我们的做法进行说明，希望能给同仁有所借鉴.我们发现习题解答书中该例子的答案有错，因此具有一定的典型性.

1 分配格的定义和判定定理

关于分配格的定义，可以按照偏序集－格－分配格的顺序来理解，其定义如下：

在判断一个具体的格是否是分配格时，只需验证（1）式（或（2）式）是否成立即可.尽管如此，注意到（1）式中a，b，c三个元素是任取的，即当且仅当对A中任意三个元素（1）式都成立时，〈A，≤〉是分配格；只要存在三个元素a0，b0，c0，不满足（1）式，就可说明〈A，≤〉不是分配格，所以当A中所含元素较多时，利用定义来判定的计算量将很大.文献［2］给出了如下一个判定定理：

定理1［2］格〈A，≤〉是分配格当且仅当A中不含与钻石格或五角格同构的子格.其中钻石格和五角格分别如图1和图2所示.

可以看出，与定义3相比，定理1相对直观便捷，因此学生大多倾向于用后者来判定.但在解题过程中，只要对该定理理解不透彻，就容易出错.下面我们举例说明.

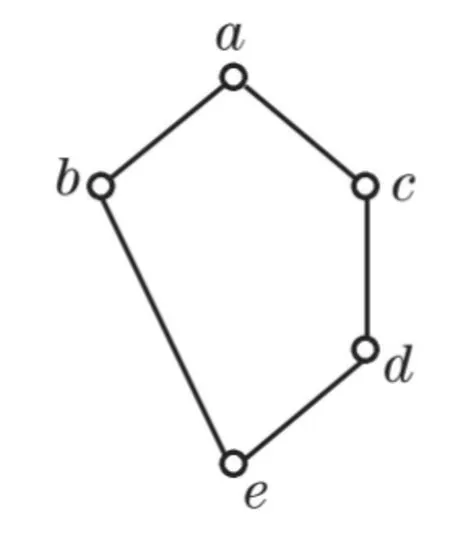
图2

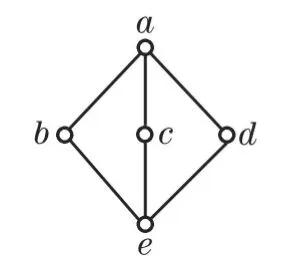
图1

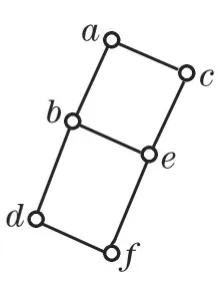
图3

2 一个典型例子

这里以文献［1］中第六章第二节习题（2）的图（a）（如图3所示）为例，学生在解这道题时出现的错误具有一定的典型性.

该题要求判断图3表示的格是否是分配格.学生很自然会想到运用定理1这样来判定：因为图3表示的格中有与五角格同构的子格，所以它不是分配格.这一错误解答相当普遍，几乎每届学生都会出现，能够得出正确结果的只是凤毛麟角.文献［1］的配套习题解答书［3］中给出的也是这一错误解答，甚至很多教师在没有深入思考的情况下也会采纳这个解法.下面结合该例子探讨如何解决学生在求解该类问题时容易出错的教学问题.

学生对答案书的迷信，加大了我们纠正错误的难度.我们发现，在教学尤其是课堂管理过程中，权威效应是不容忽视的，答案书在学生的观念中就具有一定的权威性，所以，必须通过有效的方法，引导学生自己来发现错误.既然学生具有计算机专业这一背景，我们就思考能否借助计算机这一工具来辅助教学.由于概念的原始定义一般都比较容易理解，所以可以考虑先放弃从定理1入手，而是回到原始定义尝试用定义3来判定.因为图3中的格有6个点，所以需要对120（即A36）组数据分别判断分配等式（1）是否成立.此时，手工计算很是麻烦，但可以借助计算机程序来处理.我们可以引导学生编一个通过定义来判断任意一个格是否是分配格的小程序.

由于格本质上是一种关系，注意到用哈斯图表示的关系不便于计算机实现，可以将哈斯图转化为关系矩阵，而关系矩阵就可以用程序设计语言的数组来表达.设格为〈A，≤〉，以下是我们指导学生编写的VB程序的算法：

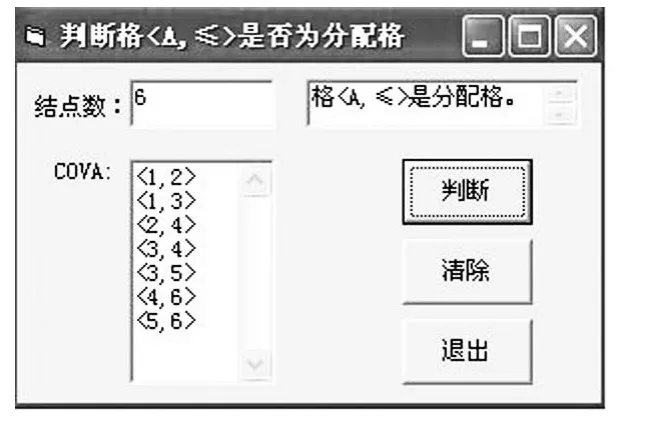
图4

在图3的格中，很多学生会提出B1＝｛a，c，d，e，f｝，B2＝｛a，b，c，d，f｝两个五元素子集与五角格同构，但它们关于∨或∧不封闭，因而不是子格.不妨考察B2，b，c∈B2，但b∧c＝e∉B2.事实上，符合子格要求的五元素子集只有B3＝｛a，b，c，e，f｝，B4＝｛a，b，d，e，f｝两个，而它们显然不与五角格同构.因此，由定理1可知图3的格是分配格.

解释完以后，可以让学生思考两个问题：

问题1 钻石格和五角格是分配格吗？为什么？

问题2 为什么定理1中一定强调子格？

对于问题1，学生利用已经编好的程序给出了如下答案：因为三元组〈b，c，d〉，〈b，d，c〉，〈c，b，d〉，〈c，d，b〉，〈d，b，c〉和〈d，c，b〉均不满足分配等式（1），所以钻石格不是分配格；同理，因为三元组〈c，b，d〉和〈c，d，b〉不满足分配等式（1），所以五角格也不是分配格.

对于问题2，学生经过讨论也给出了正确答案：一个格中若含有与五角格或钻石格同构的子格，则在该格中会出现与上述三元组地位相同的三元组，它们也不满足分配等式（1），因而该格不是分配格.

事实上，对于该问题我们还得到了另一种解法.该解法不通过定义3和定理1，而是需用到以下性质1（即文献［3］的习题6－18）：

性质1［3］分配格的任意子格仍是分配格，即设〈A，≤〉是一个分配格，〈A，∨，∧〉是由〈A，≤〉所诱导的代数系统，设〈B，≤〉是〈A，≤〉的一个子格，则〈B，≤〉也是一个分配格.

该性质的证明如下：

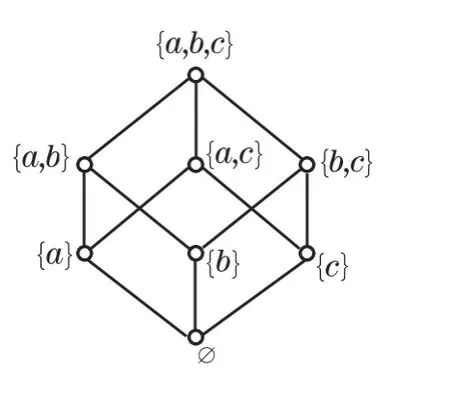
图5

若能记住一些类似于〈P（S），⊆〉的已知的分配格，在解题时，首先想到将待判定的格与这些分配格进行比较，当发现待判定的格与这些分配格的子格同构，就可以马上利用性质1判定该格是分配格了.

3 结束语

我们运用计算机这一工具，结合一个典型例子，很好地解决了分配格判定这一教学难点.我们认为这一方法可以推广到离散数学的类似教学问题中去.本文的做法也引出了一个问题，那就是如何充分利用学生的专业特点来进行教学，这值得我们思考.需要特别说明的是，在撰写此文后，发现李思泽［4］已指出过文献［3］中的这一错误，但本文给出了2种新的解法.最后还需要指出，该错误似乎没有得到重视，文献［3］2005年的印刷版仍未改正这一错误，借此机会，我们呼吁该书再版时尽快修正.

［1］左孝凌，李为鑑，刘永才.离散数学［M］.上海：上海科学技术文献出版社，2007.

［2］耿素云，屈婉玲.离散数学［M］.北京：高等教育出版社，1998.

［3］左孝凌，李为鑑，刘永才.离散数学——理论·分析·题解［M］.上海：上海科学技术文献出版社，2005：328－329.

［4］李思泽.《离散数学》（左孝凌等编）教材中习题的探讨［J］.工科数学，2001，17（6）：105－106.