兵器试验中的异常值检验

尹江丽，王琳静

(中国人民解放军装备学院基础系，北京 101416)

在兵工产品试验过程中，经常会出现这样的现象:一组重复测量的试验数据里，会出现少数几个偏差特别大的数据，这类数据称为可疑值。可疑值产生的原因主要有以下2个方面:①各种随机因素影响所致。此时，可疑值客观地反映了测量设备在特定条件下进行测量的随机波动性，与其它值属于同一总体，应当予以保留。② 由于设备工作偶然异常、外来干扰或人为操作错误等原因产生的过失误差所致。这种可疑值的分布规律和正常值的分布规律相悖，与正常值不属于同一总体，这类可疑值称为异常值，应当予以剔除［1］。本文采用假设检验的方法，对兵器试验中的异常值问题进行分析判断。

1 兵器试验中异常值检验问题描述

兵器试验中，一般很难查出可疑值产生的原因，这时只好借助于统计方法进行判别是否是异常值。用统计方法进行判别的基本思想是:给定一置信度，当误差超过这一置信度时，则认为是异常数据，应予剔除。因此，判别异常值的统计方法也是一种假设检验［2］。

兵器试验中对异常值进行检验的前提是:被检验的总体服从正态分布［3］。该问题的假设检验可以采用以下方式描述。

设 X1，X2…，Xn是取自正态总体 N(μ，σ2)的样本，其中μ未知，σ2已知或未知，将 X1，X2，…，Xn按着从小到大的顺序排列得:X(1)，X(2)，…，X(n)，这里若 X(n)或者 X(1)明显偏离其他值，则为可疑值。若 X(n)或者 X(1)与其它的 X(i)( i≠1，n)属于同一总体，则为正常值，否则为异常值，对异常值必须予以剔除，因此提出如下形式的检验:

H0:X(n)(or X(1))为正常值

H1:X(n)(or X(1))为异常值

常见的假设检验方法有很多，比如拉依达法、肖维勒法、格拉布斯法、狄克逊法、t检验法等。在兵器试验中常用的检验方法为格拉布斯法和狄克逊法。本文针对以上描述问题，重点分析这2种方法在不同条件下的异常值检验模型，并结合兵器试验的数据处理实例进行分析判断。

2 格拉布斯(Grubbs)检验法

2.1 σ2已知情况

1)对于随机变量X1，X2，…，Xn，计算样本均值¯x的值。

2)计算统计量G的值

3)对于给定的显著性水平α，用n，α查表1得βα的值。

4)若G＞βα，则拒绝H0，认为x(n)(或x(1))为异常值，应予以剔除，否则保留。

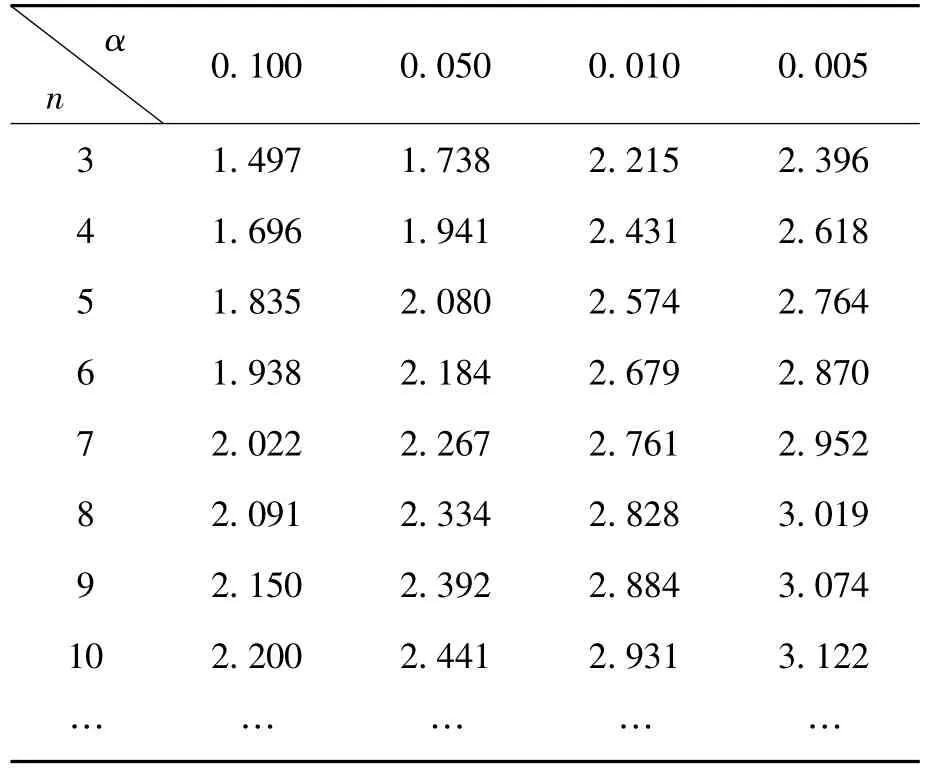
表1 G分布的临界值βα表

2.2 σ2未知情况

1)对于随机变量X1，X2，…，Xn，计算样本均值¯x和标准差S得值。

2)计算统计量Q的值

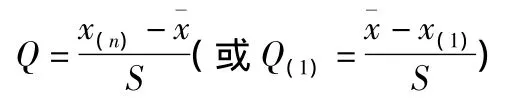
3)对于给定的显著性水平α，用n，α查表2得qα的值。

4)若Q＞qα，则拒绝H0，认为x(n)(或x(1))为异常值，应予以剔除，否则保留。

例如:某榴弹装药射角射击8发。得射程X的样本值如下(单位:m):2 179，2 177，2 184，2 185，2 173，2 158，2 163，2 146，经统计有关历史资料，在该装药该射角下，标准差σ=15 m，在显著性水平α=0.01下分析其中有无异常值。

解:在兵器试验中，认为射程X是正态分布［3］。

1)将样本值从小到大排列后发现x(1)=2 146明显偏离其他值，视为可疑值。

表2 Q分布的临界值qα表

3 狄克逊(Dixon)检验法

3.1 判断X(n)是否异常

1)计算统计量 ri(i=1，2，3，4)的值

若3≤n≤7，使用 r1;若 8≤n≤10，使用 r2;若 11≤n≤13，使用 r3;若 14≤n≤30，使用 r4。

2)对于给定的显著性水平α，用n，α查表3得rα的值。

3)若 ri＞ rα(i=1，2，3，4)，则拒绝H0，认为x(n)为异常值，应予以剔除，否则保留。

3.2 判断X(1)是否异常

把3.1中的检验统计量换为:

其他步骤同 3.1，就可以用来检验 X(1)是否为异常值［4－5］。

例如，某型号导弹落点横向偏差的数据如表4，根据经验，落点横向偏差服从正态分布，在显著性水平α=0.05下，判断是否有异常值。

解:显然x(1)=－81 910和x(7)=19 994为可疑值。由上述理论知识可知:

查表3 得 rα=0.507，显然 r'1＞ rα，r1＜ rα，故认为 x(1)为异常值，予以剔除，但没有理由认为x(7)是异常的，故应当保留。

表 3 ri(i=1，2，3，4)分布的临界值rα 表

表4 某导弹落点横向偏差的样本值

4 结束语

实例分析结果证明，假设检验方法是兵器试验中异常值检验的一种有效方法。格拉布斯法适用于剔除一个异常值，而狄克逊法一次可以剔除多个异常值，当目测估计有多个异常值时，建议使用狄克逊法，并且狄克逊法不需要计算样本的均值和标准差，方法比较简单。

［1］ 包国忱.电子装备试验数据处理［M］.北京:国防科工委司令部，1997:153－154.

［2］ 高峻.军品质量检验技术［M］.北京:国防工业出版社，2004:132－134.

［3］ 闫章更.试验数据的统计分析［M］.北京:国防工业出版社，2001:51－101.

［4］ 魏治文，程琳.几种异常值判别准则在安全检测数据处理中的应用［J］.大坝与安全，2009(1):67 －69.

［5］ 苏健，朱炬波.导引精度分析中的异常值检验［J］.飞行器测控学报，2008，27(2):62 －65.

［6］ 王君，高颖慧，王平，等.一种ICP改进算法［J］.重庆理工大学学报:自然科学版，2011(10):71－76.

［7］ 汪辉，杜红梅，杨亮.复杂电磁环境对兵器试验靶场测控装备的影响［J］.四川兵工学报，2012(8):92－94.

(责任编辑杨继森)