旋转弹链传动系统动力学仿真与振动分析

赵 洋，吴茂林

(海军工程大学 兵器工程系，武汉 430033)

链式自动化弹仓是某大口径火箭弹自动化装填系统的重要组成部分，在控制系统的作用下，由链轮驱动弹链带动弹筒到达指定位置。这种链式弹仓在每一次射击之后，弹筒内弹体数目减少，整个传动系统的质量分布和转动惯量都会发生变化，从而使得该传动系统的固有频率也随之变化，在实际使用的过程中可能会有共振现象的发生。但从目前实际使用的装备来看，尚未有控制装置调节传动系统的固有频率，来避免共振现象的发生。本文通过建立该传动系统的动力学模型，使用Matlab工具进行仿真，分析影响系统固有频率的主要影响因素，并提出了通过改变撑紧链轮弹簧刚度，来反馈调节链传动系统固有频率的思路。可有效可避免共振现象的发生，有效降低振动噪声，提高装备的稳定性和使用寿命。

1 链传动系统的动力学建模

主动轮通常在步进液压马达的驱动下按已知的运动规律做间歇运动，带动从动轮和链条沿导轨做间歇运动。针对装备的实际特点，做如下简化:

1)由于在每2个链轮之间的各个相邻弹筒上有相互啮合的凸齿，可以约束弹筒在传动链直线运动方向上的晃动和碰撞，故可采用集中质量建模的方法，将每2个链轮之间的弹丸等效成一个质量体来对传动链系统进行动力学建模研究，根据该型弹仓内传动链实际运动轨迹和具体结构特征，整个传动链上的弹丸可等效为5个质量块，主动轮与撑紧链轮等效为质量块。

2)考虑到由主动轮输入轴扭转和撑紧链轮弹簧产生的振动影响，将其分别视为无质量的扭转弹簧和连接固定端的拉伸弹簧。

3)链条是一个闭环传递机构，在多个从动轮中只有一个从动轮附有弹簧撑紧装置即撑紧链轮，其他从动轮的作用只视为改变传动链运动方向，忽略其他影响。

4)将复杂链条简化为线弹性体。

5)研究问题的范围限定在链条是在拉直的条件下。

6)链条底端有滑轮支撑，忽略摩擦力作用。

建立链传动系统模型如图1所示。

图1 链传动系统模型

图1 中，m0为撑紧链轮的质量;m1，m2，m3，m4，m5，m6为弹丸的等效质量;R0为主动链轮半径;R1为从动链轮半径;I0为撑紧链轮的转动惯量(附加负载的作用);I1为主动链轮的等效转动惯量(附加负载的作用);kθ为主动链轮输入扭转刚度;k1，k2，k3，k4，k5，k6，k7为链条的等效刚度;k0为撑紧链轮支撑弹簧刚度;Φ0为撑紧链轮的实际转角;Φ1为主动轮的实际转角;x0为撑紧链轮纵向位移;τ为为任意时刻输入的转角，τ(t)为运动规律。

忽略摩擦，则系统的动能和势能可分别表示为:

1)主动轮动能

2)撑紧链轮的动能

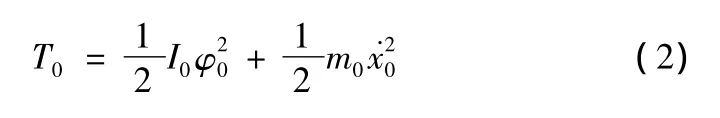
3)弹丸等效质量块的动能

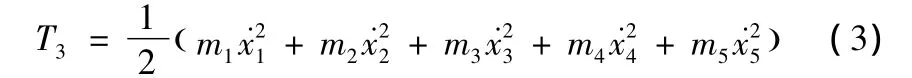
系统的总动能

系统势能

应用广义系统的拉格朗日方程，将系统动能与势能的表达式分别对广义坐标 φ1，φ0，x0，x1，x2，x3，x4，x5求导，可推导建立动力学微分方程组为

微分方程在不计阻尼的情况下含有外界激励的系统可表示为

其中:X为广义坐标向量;M、K分别为质量矩阵和刚度矩阵;F为外界激励向量。其各表达式为

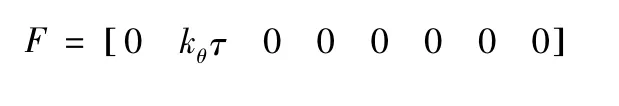
2 动力学方程求解

求解方程步骤如下:

步骤1:建立系统的运动方程组，即式(6)。

步骤2:写出特征方程，求系统固有频率，即

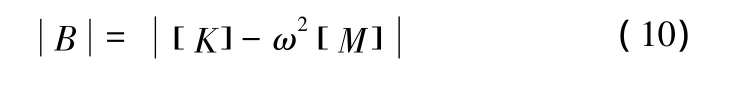
上式有非零解的条件是

所以，代入数据可求的得

步骤3:求振幅比

步骤4:求得自由振动的一般解

一般解是各固有频率对应的简谐振动叠加

3 撑紧链轮支撑弹簧变化规律与仿真结果

对图1所建的链传动系统集中质量模型应用Matlab语言编程，用上述计算方法进行求解，可求得系统的固有频率。为分析出等效质量块和撑紧链轮弹簧撑紧刚度对系统固有频率的影响，分别以等效质量块的质量分布和撑紧链轮弹簧撑紧刚度为变量，求系统固有频率的分布图。(在以等效质量块的质量分布为变量时，由于该分布情况由多种，故取其五种特殊情况进行分析，即 m1，m2，m3，m4，m5分别为0，其他质量体为满负荷时，来进行比较。)

图2所示为等效质量块的质量分布对系统高阶固有频率的影响(图中的横坐标xi表示质量体mi为0)。

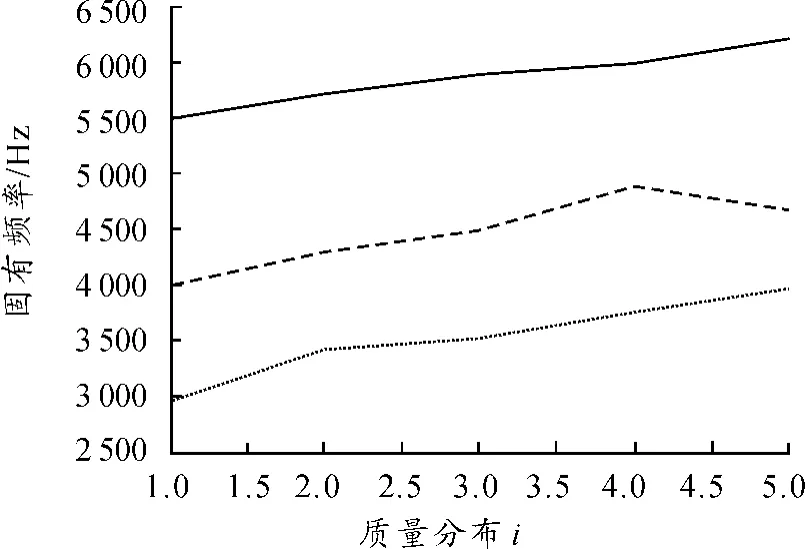
图2 等效质量块的质量分布对系统高阶固有频率的影响

图3所示为等效质量块的质量分布对系统低阶固有频率的影响(图中的横坐标xi表示质量体mi为零)。

图3 等效质量块的质量分布对系统低阶固有频率的影响

图4所示为撑紧链轮撑紧弹簧刚度对系统高阶固有频率的影响。

图4 撑紧链轮撑紧弹簧刚度对系统高阶固有频率的影响

图5所示为撑紧链轮撑紧弹簧刚度对系统低阶固有频率的影响。

图5 撑紧链轮撑紧弹簧刚度对系统低阶固有频率的影响

4 结束语

从仿真结果可以看出，等效质量块的质量分布和撑紧链轮弹簧撑紧刚度对整个链传动系统的固有频率影响较为明显。由于在弹链的运转过程中，随着弹药的增加或消耗，负载是随之变化的，整个传动系统的动力学方程的数值解也是随之变化的，即系统固有频率是随弹药的数量和位置的分布而变化，所以，装备有可能在装填弹药或射击后运作时发生共振现象。为避免共振现象的发生，在设备中设计一个具有反馈可调节撑紧链轮弹簧撑紧刚度的装置是非常必要的，这对于降低整个系统的振动、噪声和提高弹药的运转稳定性和控制输送精度是非常有效的。

［1］ 侯保林，马建伟.链式自动化弹仓的最优保性能控制算法［J］.兵工学报，2009，30(9):1164 －1169.

［2］ 毛君，师建国，张东升.重型刮板输送机动力建模与仿真［J］.煤炭学报，2008，33(1):103 －106.

［3］ 胡胜海，郭彬，邓坤秀，等.含非线性接触碰撞的大口径舰炮弹链柔性铰多体模型［J］.哈尔滨工程大学学报，2011，32(9):1217 －1222.

［4］ 盛秋峰，洪嘉振，刘铸永，等.含接触碰撞的变拓扑系统动力学仿真［J］.上海交通大学学报，2008，42(8):1222－1237.

［5］ 章定国.航炮弹链中的碰撞动力学［J］.南京理工大学学报，1995，19(3):210 －213.

［6］ 赵瑞学.某战车炮自动机关键技术研究［D］.南京:南京理工大学，2011.

［7］ 郑志峰，王义行.链传动［M］.北京:机械工业出版社，1984.

［8］ 王慧莹.步进传动链机械系统的动力学分析与应用研究［D］.天津:天津大学，2007.

［9］ 许立新.步进链传动系统的动力学仿真研究［D］.天津:天津大学，2008.

［10］李德胜.自动装弹系统的运动实现与传动性能研究［D］.天津:天津理工大学，2009.

［11］王立新，柳占雄，龙健，等.某弹链力学性能计算［J］.四川兵工学报，2011(7):16－20.

(责任编辑杨继森)