电动舵机系统建模及控制算法

潘大夫

(安徽东风机电科技股份有限公司，合肥 230022)

舵机的作用是驱动舵面偏转，控制导弹的飞行姿态和弹道［1］。随着导弹性能不断提高，对舵机系统的要求也越来越高，包括对舵机体积、质量、承载能力，以及对控制性能的要求。基于直流无刷电机(BLDCM)的舵机系统具有体积小、质量轻、输出力矩大、易维护等优点，逐步成为导弹舵机发展的主要方向［2，3］。

电动舵机系统设计的难点集中在机械传动机构的设计制造和系统控制方法。在机械传动机构部分，通常将电机输出经若干级减速放大后驱动舵轴偏转。常用减速方式有行星齿轮减速、谐波齿轮减速、蜗轮蜗杆机构减速、滚珠丝杠副减速等。其设计目的都是尽量在满足性能条件下，使执行机构体积更小、效率更高。

PID控制是工业控制领域优良的控制方法，在电动舵机控制领域也应用广泛［4］。模糊控制、鲁棒控制、最优控制等先进控制方法纷纷引入舵机控制，并取得重要应用。其中，滑模变结构控制以其快速响应、扰动不灵敏、无需系统在线辨识、物理实现简单等优点，在电动舵机控制方面具有独特的优势［5］。因此，本文以某电动舵机为对象，进行系统建模与分析，设计出满足指标要求的滑模控制器。

1 电动舵机系统设计

电动舵机系统是控制导弹舵面偏转的伺服系统，主要由舵机控制器、PWM功率模块、伺服电机、减速器和角位置传感器(反馈电位计)等部分组成，如图1所示。

图1 电动舵机系统结构

电动舵机控制器采集舵机指令和舵机反馈信号，经控制器综合、处理后生成控制信号，然后进行功率放大驱动电机，直流伺服电机经减速器后带动舵片偏转，舵片偏转角度由电位计反馈给控制器构成控制闭环。

本文设计的电动舵机系统性能指标应达到表1中要求。

表1 电动舵机性能指标

经分析计算，选用Maxon直流无刷电机RE25－118752，该电机主要性能参数如下:

电机电阻为2.32 Ω，堵转转矩为243 mNm，额定转矩为26.3 mNm，最大允许转速为8 330 r/min，转矩常数为23.4 m Nm/A，速度常数为408 rpm/V，机械时间常数为4.55 ms，转子惯量为10.8 gcm2。舵机传动机构采用谐波齿轮+锥齿轮，系统传动比取i=190，效率η=0.6。

2 直流无刷电动舵机建模

2.1 直流无刷电机建模

文中［3］经过数学模型推导，得出直流无刷电机的数学模型如图2所示:

图2 直流无刷电机模型

2.2 电动舵机系统模型

驱动器将控制器输出的控制信号进行功率放大后，驱动直流无刷电机，在系统中是一个比例环节k1;减速器把直流电机输出的转角减速后带动舵片偏转，也是一个比例环节k2。这里，令K=k1×k2×K*。此外，角位置反馈电位计把舵片偏转位置转转换成电信号给控制系统综合，也是比例环节，记做 Kf。

直流无刷电机舵机模型如图3所示。

图3 电机舵机系统模型简化结构

简化后的电动舵机传递函数写成微分方程形式:

根据选定的直流无刷电机性能参数和舵机设计指标要求，得出电动舵机理论模型参数:

3 电动舵机控制器设计

3.1 PID 控制器

PID控制是经典控制策略，由于算法简单、鲁棒性好和可靠性高，被广泛应用于过程控制和运动控制。因此，对环境复杂、系统工作参数易变的电动舵机系统，PID控制方法也是可取的。

其控制规律如下:

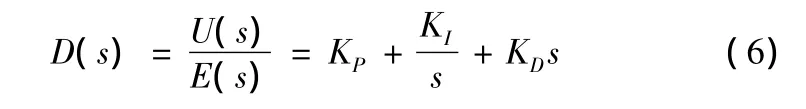
3.2 滑模变结构控制器

滑模变结构控制(sliding mode control，SMC)是变结构控制系统(VSS)的一种控制方法。该方法与常规控制的根本区别在于系统的“结构”并不固定，可以在动态过程中，根据系统当前的状态(如偏差及其各阶导数等)，有目的地不断变化，迫使系统按照预定“滑动模态”的状态轨迹运动。SMC已成为控制系统的一种普遍设计方法，适用于电机控制、机器人控制与飞机控制等，使系统在受到参数摄动和外干扰时

传递函数表示:具有很好的鲁棒性［6，7］。

这里，针对电动舵机模型式(3)，进行基于指数渐进律的滑模变结构控制器设计:

被控对象微分方程:

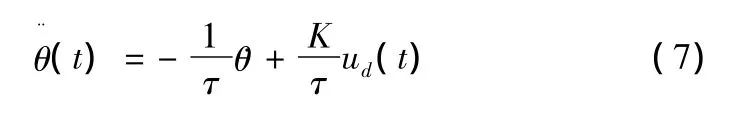
跟踪误差:

滑模函数:s(t)=ce(t)+˙e(t)，其中c＞0，满足Hurwitz条件。则:

采用指数趋近律，有:

结合式(9)和式(10)，得:

基于趋近律的滑模控制器:

4 仿真分析

在图3舵机系统模型中，参数设计取K=20，Kf=0.65，进行住址分析［8］。在输入幅度2°，频率5 Hz和10 Hz正弦角位置信号时，系统响应结果如图4、图5所示。此时，输入5 Hz信号响应幅度1.5°，相位滞后47°;10 Hz响应幅度仅0.94°，相位滞后达 72°。

图4 输入5 Hz时的响应

4.1 经典PID控制算法

根据电动舵机系统性能指标要求，设计PID控制器:

在输入幅度2°，频率5 Hz和10 Hz正弦角位置信号时，系统响应结果如图6、图7所示。

仿真结果:5 Hz响应幅度1.98°，相位滞后15°;10 Hz响应幅度1.96°，相位滞后达32°。采用PID控制，不能满足输出达到幅值2°、10 Hz的指标要求。

图5 输入10 Hz时的响应

图6 输入5 Hz时PID响应

图7 输入10 Hz时PID响应

4.2 趋近律滑模变结构控制算法

在基于趋近律的滑模控制器式(12)，取τ=0.004 2，c=15，ε =5，k=10。在输入幅度 2°，频率 5 Hz和 10 Hz正弦角位置信号时，系统响应结果如图8、图9所示。

仿真结果:5 Hz响应幅度2°，相位滞后1.3°;10 Hz响应幅度1.99°，相位滞后达5°。可见，采用指数趋近律滑模变结构控制，舵机系统能满足输出达到幅值2°、10 Hz的指标要求。

图8 指数趋近律滑模控制响应1

图9 指数趋近律滑模控制响应2

5 结束语

本文以某电动舵机指标要求为依据，对直流无刷电动舵机系统建模进行了分析与推导，从PID与滑模变结构控制两个方面，对满足舵系统指标要求的控制器进行了设计、仿真，实验结果表明，基于趋近律的滑模变结构控制器具有响应快、跟踪精度高的优点，满足系统设计要求。

［1］ 雷虎民.导弹制导与控制原理［M］.北京:国防工业出版社，2006.

［2］ 张琛.直流无刷电动机原理及应用［M］.北京:机械工业出版社，2004.

［3］ 刘刚，王志强，房建成.永磁无刷直流电机控制技术与应用［M］.北京:机械工业出版社，2008.

［4］ 胡寿松.自动控制原理［M］.北京:科学出版社，2008.

［5］ 胡剑波，庄开宇.高级变结构控制理论及应用［M］.西安:西北工业大学出版社，2008.

［6］ 胡跃明.变结构控制理论与应用［M］.北京:科学出版社，2003.

［7］ 刘金琨.滑模变结构控制MATLAB仿真［M］.北京:清华大学出版社，2005.

［8］ 周品，赵新芬.MATLAB数学建模与仿真［M］.北京:国防工业出版社，2009.

(责任编辑周江川)