系统规模对群体行为的效果*

易奇志 杜 焰 周天寿

1)(江西师范大学数学与信息科学学院，南昌 330022)

2)(江西师范大学化学与化工学院，南昌 330022)

3)(中山大学数学与计算科学学院，广州 510275)

(2012年11月29日收到;2013年2月6日收到修改稿)

1 引言

细胞生存于复杂的环境中，能够感应来自其他细胞的生物信号，与周围的细胞或环境形成各种相互作用.对于由多个相互作用的细胞组成的群体系统，其群体行为并不仅仅依赖于单个细胞水平的动力学，而更多的是依赖于细胞之间相互作用的方式与效果[1-5].事实上，细胞之间的相互作用可以有效地调节和影响细胞的群体行为，如引起完全相同的细胞分化[6];又如P19细胞允许聚集时可以有效地分化成骨骼的肌肉(这是因为细胞聚集形成的相互作用可以调节转录因子myoD诱导的骨骼肌浆蛋白)[7].在细胞间有通讯的多细胞系统中，细胞之间的信息交换与整合会引起细胞群体协作响应，导致多细胞系统展示出各种有趣的现象，如生物节律[8]，细胞斑图[9-15]，以及同步、聚类、多稳态共存、多节律性等[14-21].

多细胞现象(表现为群体行为)，除了与细胞之间的通讯方式、信号整合构件(又称为顺式调控构建)有关外，还可能与相互作用的细胞数目有关.例如，在生物体发育过程中，细胞的分裂会引起细胞数目的增加;在活的有机体内，细菌群体的增殖与扩张会引起细菌数目的增加.反过来，细胞数目的增加会引起细胞之间通信概率的增加，从而有可能影响和改变原有多细胞系统的群体动力学行为.例如，Kaneko等[3]模拟了一群有生化网络相互作用的细胞，包含细胞分裂过程，发现当细胞数目到达某个阈值时，分裂导致几乎完全相同的细胞同步振动.随着数目的进一步增加，同步振动逐渐消失，导致细胞分成几个具有不同振动相位的子类，从而导致不同振幅的聚类振动.他们由此提出了细胞分化的同构异素多元化理论(isologous diversification).又如，Nakajima等[1]设计了一个核心的基因调控模块，并设计了细胞之间的3种不同方式的相互作用，分别对应于3个不同模型.他们展示出在这3种作用方式下细胞状态是如何随细胞总数的变化而分化.更细化地，他们显示出：对第一种作用方式，细胞命运由细胞总数决定，即随着总数的增加，细胞群体从1聚类切换到2聚类，再切换到另一个1聚类;第二种作用方式能够使得细胞状态出现多元化，即细胞数目增加到适当范围时，1聚类与2聚类可以共存.这一理论模型所描述的现象与发育生物学上所观察的现象[22,23]基本一致.此外，Koseska[20]考察了一个由群体感应机制耦合的压制振动子组成的多细胞系统，发现系统规模的增大不仅使异质平衡态的稳定性区域扩大，而且使其吸引域也扩大.他由此提出了多细胞群体通过聚类进行协作分化的观点.总之，系统规模的大小对于细胞采用何种策略取得群体行为起着非常关键的作用.研究细胞数目对于多细胞系统群体动力学行为的影响不仅具有重要的实际意义，而且有助于我们理解种群在扩张情形时的协作行为.

在文献[21]中，我们研究了细胞通讯在由群体感应机制耦合的组合振子的多细胞系统中的作用，发现细胞通讯能够诱导耦合系统的多稳性和多节律性.尽管这一重要的定性结论并不受振子数目的影响，但鉴于细胞数目的增加可能会导致细胞群体动力学发生各种定性的或定量的改变，因此在前文工作的基础上，这里我们将进一步调查细胞数目的改变是如何影响这个多细胞系统的群体行为的，特别关注细胞数目(或系统规模)的增加如何影响聚类(clustering)行为.这里的工作能够看成是前一工作的延伸，但获得了更多有趣且有意义的结果.

为理解起见，这里我们简单地解释聚类.聚类是一种稳定的动力学状态，它可能包含若干个子群体，每个子群体具有相同或几乎相同的行为.聚类在由大量相互作用单元的生物、化学、物理和社会系统中普遍存在，并吸引了众多研究者的广泛关注[1-3,14,15,19,20,24-27].在生物学上，聚类与细胞分化密切相关.多细胞生物系统的细胞分化机制极其复杂，一种普遍的观点是细胞根据成形素浓度梯度设定其位置信息进行分化[28].然而，即使在相同的环境条件下，相同的细胞仍可以展示不同的表型(phenotype)，从而由相同细胞组成的群体也可呈现出某种异质性(heterogeneity)，主要表现在可能存在几个子类，且每一个子类中的细胞表现出有组织的群体行为.正如文献[2，20]所指出的，动力学聚类为细胞分化提供了另一种可能的机制或解释.

本文主要关注系统规模对于组合振子多细胞系统两种聚类行为——平衡态聚类和振动聚类的影响.利用分岔分析和数值模拟，我们发现：细胞数目的增加可以改变异质平衡态的稳定性区间的大小，并诱导新的聚类行为;对于适当的细胞密度，细胞数目的增加有利于扩大异质平衡态的吸引域，特别是，当细胞数目充分大时，异质平衡态占主导地位，几乎以概率1出现，表明细胞分化可能与细胞数目有密切关系;细胞数目的增加极大地丰富了平衡态聚类和振动聚类的表现形式和共存方式，为生物体的适应性和多功能性提供了良好的基础.

2 数学模型

这里，我们仍采用我们最近的工作[21]中的合成基因调控网络模型。在这一模型中，首先，单个振子是由压制振动子和松弛振子通过整合而成的组合振子 (见图 1)，其中 U(TetR)，V(CI)和 W(LacI)分别是三个基因u(tetR)，v(cI)和w(lacI)的产物，自体诱导物(一种小的信号分子)W的动力学可以通过在相应方程中引入一个小参数而减慢;其次，振子之间通过群体感应机制耦合而构成多细胞系统，其中信号分子可以扩散到群体中每一个细胞的内部，并调控目标基因的表达(关于模型的详细描述，见文献[21]).类似于文献[21]的简化，我们合并转录、翻译过程为单步过程，并采用拟平衡态假设，来建立数学模型，由此得到如下多细胞系统模型：

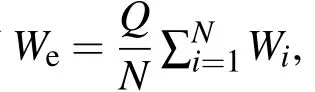
图1 组合振子的示意图

3 系统规模对聚类行为的效果

在下面的分析中，我们将主要从平衡态聚类(steady state clustering)、振动聚类(oscillatory clustering)两个角度来刻画系统规模N对多细胞系统聚类行为的影响.我们指出：平衡态聚类实际上是系统形成异质平衡态(inhomogeneous steady state，IHSS)，更确切地说，在所有细胞中，对应成分(如W等)取两种不同的常数值.通常，N个耦合振子在平衡态聚类中有N-1种不同的分布.特别地，当考虑耦合系统中的某个成分时，例如，Wi(i=1,2,···,N)，假设m个W处于高的浓度状态(记为mU)，而其余的N-m个W 处于低的浓度状态(记为(N-m)L)，其中m可以取1到N-1之间的值，那么我们说系统具有异质平衡态，并把这种异质平衡态模式记为mU|(N-m)L.与异质平衡态相对的是同质平衡态(homogeneous steady state，HSS)，是指所有细胞中对应成分取相同的常数值.振动聚类是指系统中的所有单元分成若干组，每一组内的单元都有完全相同的状态，即以相同的振幅完全同步地振动.对于振动聚类，聚类模式更为复杂，可以按振幅和相位的不同分成不同的类(类的数目可以超过2，我们将在后面给出详细的解释).这些动力学聚类是理解细胞分化的重要基础.在下面，我们将采用分岔分析和数值模拟来展示和解释我们的结果，并用到缩写符号：PB代表叉形分岔，LP代表极限点分岔或鞍结分岔，HB代表Hopf分岔.

3.1 改变细胞数目对平衡态聚类稳定性区间的影响

本小节考察细胞数目的增加对于平衡态聚类的影响.为此，我们对耦合系统的规模做一个微小的改变，把系统从包含2个相同细胞扩充为包含3个或4个相同细胞.以细胞密度Q作为分岔参数，作W1关于Q的分岔图.为了便于比较，我们只展示与稳定的异质平衡态(IHSS，即平衡态聚类)有关的分岔图，见图2(a)—(c).对于N=2的情形，当Q介于LP1和LP2之间时，耦合系统处于稳定的IHSS状态.此时，IHSS状态只有一种可能的分布，即1U|1L或两个振子中W的浓度一个处于高状态，一个处于低状态(见图2(a)中的粗虚线).对于N=3的情形，存在两种不同的稳定聚类模式(见图2(b)中的粗虚线)：2U|1L位于LP1与PB1之间(Q∈[0.1414,0.3679])，1U|2L位于PB2与LP2之间(Q∈[0.159,0.4671]).注意到这两种不同模式的聚类位于不同的分岔分支上，因此IHSS的稳定性区间为这两种模式的存在区间的并集Q∈[0.1414,0.4671]，相比N=2的情形，其IHSS的稳定性区间Q∈[0.1493,0.4119](见图2(a)中的粗虚线)，有明显的扩大(≈24.03%).当N=4时，有三种不同模式的稳定聚类(见图2(c)中的粗虚线)，从左到右依次是：3U|1L位于LP1与LP2之间(Q∈[0.1378,0.35])，2U|2L位于PB1与PB2之间(Q∈[0.1489,0.4115])，及1U|3L位于LP3与HB1之间(Q∈[0.1624,0.446]).此时，IHSS的稳定性区间为Q∈[0.1378,0.446]，它的长度比N=3时的长度稍微小一点(≈5.37%)，但比N=2时的长度要大.然而，对于N=4的情形，有一种新奇的现象发生在聚类状态1U|3L所在的分支上.具体说来，发生在HB1处的Hopf分岔引起了一个简单的周期1振动(见图2(c)中的粗点线)，它存在于HB1(Q=0.446)到LP4(Q=0.4807)之间的区间.此时，4个振子聚成两类：1个振子处于高的浓度状态，以较小的振幅振动;3个振子处于低的浓度状态，以较大的振幅同步振动.

注意，对于N≥3的情形，有N-1种不同模式的平衡态聚类，这些聚类模式在一定的范围内可以共存，系统最终演化到哪种IHSS状态，取决于初始条件.例如，在N=4时，三种IHSS状态：3U|1L，2U|2L和1U|3L可以在LP3和LP2之间共存(见图2(c)).这三种分布的蛋白质浓度水平显示了轻微的差别，这种差别可以看成是细胞群体的一种典型适应性，意味着当环境条件发生变化时，细胞群体容易调节其状态分布，以便最优地适应环境.

图2 描绘稳定的异质平衡态(IHSS)的分岔图，细胞数目分别为：(a)N=2;(b)N=3;(c)N=4.这里，粗虚线代表各种稳定模式的IHSS，细实线代表不稳定的平衡态，(c)中的粗点线代表简单周期1的稳定振动，图中4个振子按成分W的浓度聚成两类：1个振子在高状态以小振幅振动，3个完全同步的振子处于低状态，以较大的振幅振动(这个分岔图并没有显示出所有的分岔信息，只显示了与当前讨论相关的部分.符号的缩写见正文)

由上可见，细胞数目小的改变也能引起耦合系统聚类行为的定量或定性变化，表现为细胞数目的变化可以调节平衡态聚类的稳定性区间的大小，还可以导致新的聚类现象即振动聚类的发生.

3.2 改变细胞数目对平衡态聚类的吸引域的影响

现在，我们对系统规模做更大幅度的增加，将系统扩充为中等规模，即系统由20个相同的细胞组成.我们将探讨和比较N=2和N=20这两种情况下平衡聚类状态的吸引域的异同.为此，我们让细胞密度于[0,1]之间变化，其余系统参数值如前所述设置.对于每一种细胞数目N，随机产生三个蛋白质U，V，W的初始条件，使之服从区间[0,2]上的均匀分布，通过直接的数值计算，可得到200组耦合振子所有成分的时间序列，然后根据每种情况下的200组时间序列数据统计各种稳定吸引子的数目：同质平衡态(HSS)，异质平衡态(IHSS)及振动(oscillation).通过这一方法，我们可以探测每一个有统计意义的稳定吸引子，进一步得到稳定性区域关于Q的依赖性(见图3).此图表明：系统规模的增加扩大了异质平衡态的稳定性区间，并且明显地扩大了异质平衡态的吸引域，但吸引域的扩大以同质平衡态吸引域的缩小为代价(比较图3(a)和(b)中异质平衡态区域的边界).

图3 本图表明系统规模对于动力学区域分布的影响(当细胞密度在[0,1]区间内变化时，对于N=2(a)和N=20(b)中的每一种情况都有三种动力学区域：同质平衡态(HSS)，异质平衡态(IHSS)和振动(oscillation)，但是在前两种情况下吸引域的边界有些不同，表现为：系统规模的增加扩大了异质平衡态的稳定性区间，并且扩大了异质平衡态的吸引域)

下一步，我们对于N=2时HSS与IHSS共存的区间上分别任选一个Q的值(见图3(a))，例如，取Q=0.25,0.4，对于这两个Q值，我们分别研究系统规模的增加对于HSS和IHSS等动力学状态的分布有何影响.为此，对于每一种细胞数目N，我们采用前面的方法，随机产生200组蛋白质浓度的初始条件进行计算，可得到200组耦合振子所有成分的时间序列，根据这200组时间序列，可以计算出稳定吸引子HSS和IHSS发生的次数.这样，我们可以探测出每一种N对应的具有统计意义的稳定吸引子.

图4详细地表明：对于两个给定的细胞密度(Q=0.25和Q=0.40)，系统规模对动力学状态分布的效果.两种情况拥有某些共同的特征：当细胞数目少量增加时，通过随机初始条件到达IHSS的概率明显单调地增加，且是以减少HSS的概率为代价的;当细胞数目继续增加时，IHSS的概率有增大的趋势，但不是单调地增加而是有所涨落;当细胞数目增加到充分大时，IHSS完全占主导地位，HSS几乎不出现.两者的区别在于：随着细胞数目的增加，异质平衡态趋于概率1的速度稍有差别.具体说来，Q=0.25的情形要比Q=0.40的情形趋于1的速度快一点.这些结果说明细胞数目的增加有利于扩大平衡态聚类的吸引域，这也意味着细胞分化可能与细胞数目的大小有密切关系.

3.3 改变细胞数目对聚类模式及共存方式的影响

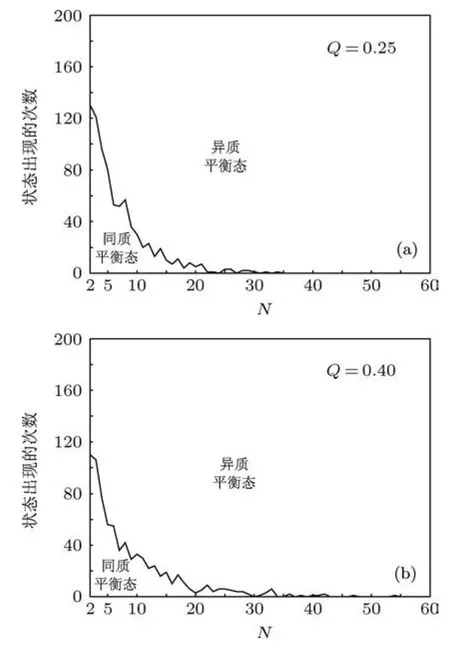
图4 当细胞密度Q被固定为 (a)Q=0.25;(b)Q=0.40时，细胞数目的增加对动力学状态(同质平衡态(HSS)和异质平衡态(IHSS))的分布产生的效果(这两种情况具有某些共同的特征：当细胞数目少量增加时，通过随机初始条件到达IHSS的概率明显单调地增加，但是以减少HSS的概率为代价的;当细胞数目继续增加时，IHSS的概率有增大的趋势，但会出现涨落;当细胞数目增加到充分大时，IHSS完全占主导地位，HSS几乎不出现)

通过数值计算，我们不难发现细胞数目的增加可以导致更丰富的平衡态聚类和振动聚类的模式及其共存方式.现以N=2和N=20的情况进行比较来说明.图5展示了20个耦合振子随细胞密度变化而出现的平衡态聚类和振动聚类.首先，随着细胞数目(N)的增加，平衡态聚类的模式(N-1种)增加，且不同的IHSS共存的方式也更加多样化.对于N=20的情形，当Q=0.36时，四种不同的IHSS状态可以共存(见图5(a)—(d)).其次，振动聚类共存的方式也更多样化.对于N=20的情形，我们观察到几种周期振动的共存，如Q=0.9时反相周期2振动和不对称周期2振动的共存(见图5(f)，(g))，以及Q=0.82时不对称1111混合模式振动和不对称1211混合模式振动的共存(见图5(i)，(j))，这些共存的方式在N=2的情况下对于所有的Q∈[0,1]都没有观察到;同时，也观察到了与N=2类似的几种振动聚类模式，如Q=0.43时的同相周期1振动，Q=0.76时的对称12111213MMO，Q=0.51时的拟周期阵发振动以及Q=0.6时的混沌阵发振动(分别见图5(e)，(h)，(k)和(l)).此外，系统规模的适当增加也使得异质平衡态可以和周期解共存(见图3(b))，这种情况在N=2时不发生.

事实上，通过对振动聚类的仔细研究，我们发现，除了图5(f)—(k)中展示的各种周期和拟周期振动聚类外，还有很多种其他的振动聚类模式，这是由于耦合系统中的各个振子可以按照振幅和相位使振动聚成不同的类.振幅不同可以导致聚类，振幅相同而相位有差异也可以导致聚类，从而对于N≥3的系统，在振动中可以形成超过两类的多个子类，这与平衡态聚类只有两个子类不同.此外，振动方式的差异(如周期1振动、周期2振动、混合模式振动等方式)和细胞在不同类之间的分布情况使得振动聚类的表现形式极为丰富，从而也使得不同模式的聚类的共存方式更加多样化.下面我们以N=20，Q=0.48的情况为例进行说明.

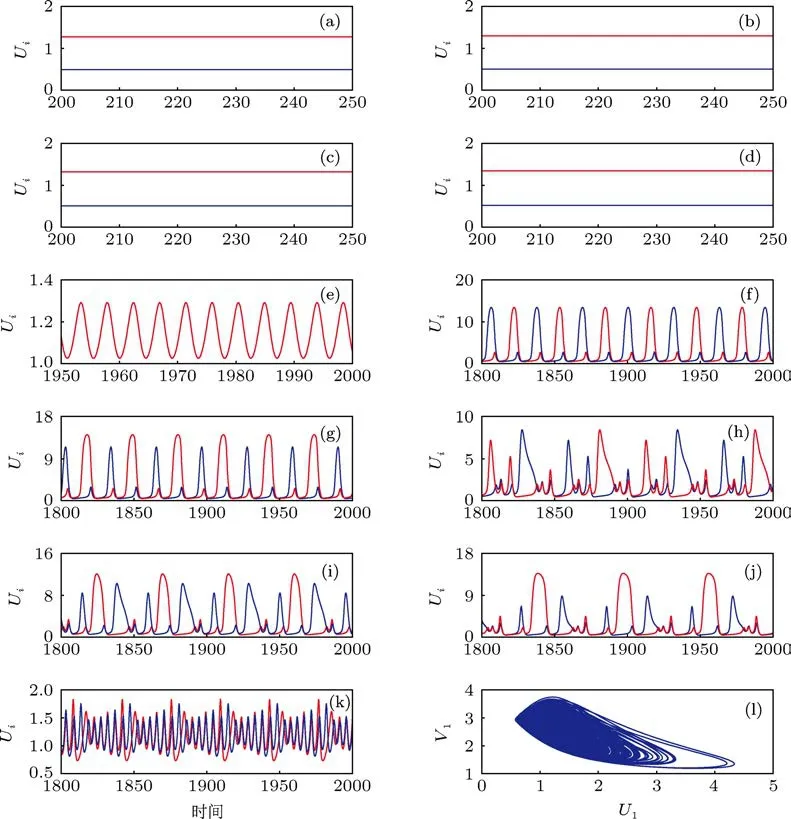
图5 20个耦合的组合振子出现的平衡态聚类及振动聚类：(a)—(d)Q=0.36时有四种具有不同分布的异质平衡态共存：(a)10U|10L;(b)9U|11L;(c)8U|12L;(d)7U|13L;(e)—(j)多模式的振动聚类：(e)Q=0.43时的同相周期1振动，(f)，(g)Q=0.9时的反相周期2振动和不对称周期2振动，(h)—(j)三种类型的混合模式振动：(h)Q=0.76时的对称12111213MMO，(i)Q=0.82时的不对称1111MMO，(j)Q=0.82时的不对称1211MMO;(k)，(l)两种模式的阵发振动，其中(k)对应于Q=0.51时的拟周期阵发振动，(l)对应于Q=0.6时的混沌阵发振动

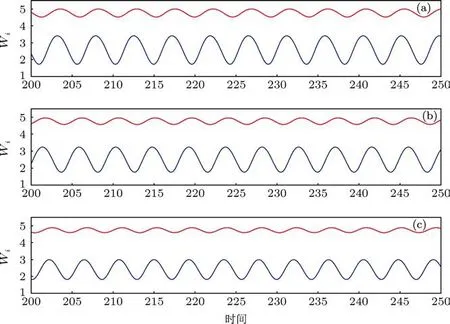
图6 当Q=0.48时，20个振子形成三种不同模式的不对称周期1的聚类振动，在上下两类中细胞数目的分布分别为(a)3：17;(b)4：16;(c)5：15

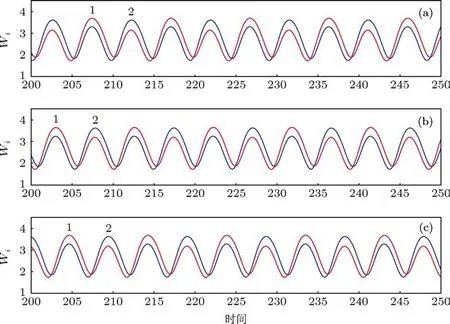
图7 当Q=0.48时，20个振子形成三种不同模式的不对称周期2的聚类振动，在第1类和第2类中细胞数目的分布分别为(a)7：13;(b)9：11;(c)8：12

图6展示了20个振子以三种不同的不对称周期1的方式振动，此时振子聚成两类，上下两类之间细胞数目的分布分别是 3：17，4：16 和 5：15. 图 7则展示了不同于图6的其他形式的振动聚类，尽管20个振子分别聚成两类，两类之间的细胞数目之比为 7：13，9：11 和 8：12，但是振动是以不对称周期 2的方式进行(在图7的每个子图中两类细胞的振幅有细微的区别).图8展示了四种更为复杂的振动聚类，此时20个振子聚成三类，细胞在第1类、第2类和第 3 类之间的分布分别为 9：10：1，8：10：2，8：11：1和9：9：2.在这里，前三种情形中第1类和第2类的振幅有细微的差别，但是第4种情形中第1类和第2类的振幅相等但相位不同.注意：对于N=20，Q=0.48的系统，按照3.2节所述的方法随机产生初始浓度进行200次的计算，我们发现除了上述展示的振动聚类之外，还有其他的振动聚类模式存在，但是经统计，图6中的三种振动聚类模式发生的频率最高，共出现了90次，其中又以图6(b)中的方式出现最为频繁(200次中出现44次)，图8中的四种振动聚类的发生也较为频繁.图6至图8中的这些状态和其他未显示的状态在N=20，Q=0.48的系统中共存，系统最终演化到哪个状态取决于初始条件，某种状态出现频率的高低与这种状态吸引域的大小有关.

系统规模的增加大大丰富了平衡态聚类与振动聚类的表现形式，为细胞的分化和多功能性提供了良好的基础，多种稳定的动力学状态的共存有效地提高了生物体适应环境的能力.

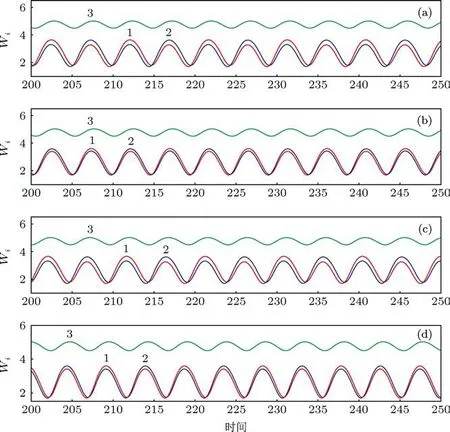
图8 当Q=0.48时，20个振子形成四种不同模式的复杂的振动聚类，在第1类、第2类和第3类中细胞数目的分布分别为(a)9：10：1;(b)8：10：2;(c)8：11：1;(d)9：9：2

4 结论与讨论

对于一个由群体感应机制耦合而成的组合振子多细胞系统，我们已经考察了细胞数目的增加对于系统动力学行为的影响，聚焦于细胞数目对平衡态聚类和振动聚类的影响.通过细致的分析，我们发现：首先，细胞数目即使少量的增加也会引起异质平衡态的稳定性区间的大小的明显改变，并诱导出新的聚类现象;其次，细胞数目的增加有利于扩大异质平衡态的吸引域，且当细胞数目增加到充分大时，IHSS占主导地位，同质平衡态几乎不出现，表明细胞分化依赖于系统规模的大小;最后，细胞数目的增加极大地丰富了平衡态聚类和振动聚类的表现形式和共存方式，为细胞分化和生物体的多功能性提供了基础，也提高了系统对环境的适应性.

动力学聚类是细胞内部动力学与细胞之间相互作用的共同结果，为细胞分化提供了一种新的机制.如何把这种机制和成形素梯度的细胞分化机制结合起来考虑，对于理解多细胞生物体的发育可能是非常重要的.保持细胞之间的相互作用，仅由于细胞的增殖引起系统规模的增加，通过动力学聚类导致细胞分化的可能性提高，这种机制是容易达到的，因为它对成形素没有要求，对于基因调控网络的参数也不需要精细的调节，从进化论的观点来看，这是非常有用的.然而，在更真实的情形，何种机制导致细胞分化还不清楚.

最后指出：我们的模型在几个方面进行了简化.首先，没有考虑详细的生物过程，把转录、翻译、启动子结合等过程合并成了一步，并且没有考虑组合调控的效果[14,15].其次，忽略了一些生物因素，如细胞的多样性，基因表达过程中固有的随机涨落，信息传输过程中的时间滞后，转录因子协作性的效果等等.这些方面可能对于规模增长的群体动力学行为产生重要的影响[20,34-39]，值得进一步的探究.

[1]Nakajima A，KanekoK 2008 J.Theor.Biol.253 779

[2]KanenoK，YomoT 1994 Physica D 75 89

[3]KanekoK，YomoT 1997 B.Math.Biol.59 139

[4]Wang J W，Chen A M，Zhang J J，Yuan Z J，Zhou T S 2009 Chin.Phys.B 18 1294

[5]Wang B H，Lu Q S，Lv S J，Lang X F 2009 Chin.Phys.B 18 872

[6]Greenwald I，Rubin G M 1992 Cell68 271

[7]Armour C，Garson K，McBurney M W 1999 Exp.CellRes.251 79

[8]Garcia-OjalvoJ，Elowitz M B，Strogatz S H 2004 Proc.Natl.Acad.Sci.U.S.A.101 10955

[9]Blair S S 2007 Annu.Rev.CellDev.Biol.23 293

[10]Fields R D，Burnstock G 2006 Nat.Rev.Neurosci.7 423

[11]Scherrer R，ShullV 1986 Can.J.Microbiol.32 607

[12]Ben-Jacob E，Cohen I，Shochet O，Tenenbaum A，Czirok A，Vicsek T 1995 Phys.Rev.Lett.75 2899

[13]Basu S，Gerchman Y，Collins C H，Arnold F H，Weiss R 2005 Nature 434 1130

[14]Zhang J J，Yuan Z J，Zhou T S 2009 Phys.Rev.E 79 041903

[15]YiQ Z，Zhang J J，Yuan Z J，Zhou T S 2010 Eur.Phys.J.B 75 365

[16]McMillen D，KopellN，Hasty J，Collins J 2002 Proc.Natl.Acad.Sci.U.S.A.99 679

[17]Ullner E，Koseska A，Kurths J，Volkov E，Kantz H，Garca-OjalvoJ 2008 Phys.Rev.E 78 031904

[18]Ullner E，Zaikin A，Volkov E I，Garca-OjalvoJ 2007 Phys.Rev.Lett.99 148103

[19]Koseska A，Volkov E，Kurths J 2007 Phys.Rev.E 75 031916

[20]Koseska A，Ullner E，Volkov E，Kurths J，Garca-OjalvoJ 2010 J.Theor.Biol.263 189

[21]YiQ Z，Zhou T S 2011 Phys.Rev.E 83 051907

[22]Gurdon J，Lemaire P，KatoK 1993 Cell75 831

[23]Shimuta K，NakajoN，UtoK，HayanoY，OkazakiK，Sagata N 2002 EMBO J.21 3694

[24]Okuda K 1993 Physica D(Amsterdam)63 424

[25]Golomb D，HanselD，Shraiman B，Sompolinsky H 1992 Phys.Rev.A 45 3516

[26]Taylor A F，Kapetanopoulos P，Whitaker B J，Toth R，BullL，Tinsley M R 2008 Phys.Rev.Lett.100 214101

[27]KuramotoY 1984 Chemicaloscillations,waves and turbulence(Berlin：Springer-Verlag)

[28]Tabata T，TakeiY 2004 Development 131 703

[29]Zhou T S，Zhang J J，Yuan Z J，Chen L N 2008 Chaos 18 037126

[30]http：//www.math.pitt.edu/bard/xpp/xpp.html.

[31]Ermentrout B 2002 Simulating,analyzing and animating dynamicalsystems：A guide toXppaut for researchers and students(software,environment and tools)1st ed.(Philadephia，PA：SIAM Press)

[32]Krupa M，Popovic N，KopellN，Rotstein H G 2008 Chaos 18 015106

[33]Izhikevich E M 2000 Int.J.Bifurcat.Chaos 10 1171

[34]Zhou T S，Chen L N，Aihara K 2005 Phys.Rev.Lett.95 178103

[35]Koseska A，Volkov E，Kurths J 2009 EuroPhys.Lett.85 28002

[36]Koseska A，Volkov E，Kurths J 2010 Chaos 20 023132

[37]Smolen P，Baxter D A，Byrne J H 2002 Biophys.J.83 2349

[38]Song H，Smolen P，Av-Ron E，Douglas D A，Byrne J H 2007 Biophys.J.92 3407

[39]Potapov I，Volkov E，Kuznetsov A 2011 Phys.Rev.E 83 031901