简谐势阱中含时散射调制造成有（无）阻尼玻色爱因斯坦凝聚体的共振现象

刘超飞，万文娟，张赣源

（江西理工大学，a.理学院；b.应用科学学院，江西赣州341000）

简谐势阱中含时散射调制造成有（无）阻尼玻色爱因斯坦凝聚体的共振现象

刘超飞a，万文娟b，张赣源b

（江西理工大学，a.理学院；b.应用科学学院，江西赣州341000）

通过周期性调节原子间的散射长度，数值模拟了有阻尼与无阻尼两种情况下玻色爱因斯坦凝聚体中的共振效应.研究发现阻尼效应导致共振驱动频率下降和共振区间变窄.能量的相互转化在数值上形成的交差现象可以显示凝聚体是否处于共振状态，以及阻尼效应带来的区别.阻尼效应致使凝聚体出现共振时的动能受到抑制，从而导致两种情况下共振现象的差异.

玻色爱因斯坦凝聚；共振；阻尼

1 Introduction

The experimental observation of dilute atomic Bose-Einstein condensate（BEC）has stimulated extensive studies of the nonlinear matter waves.One of the great interests is how the interatomic interaction affects the properties of BECs.It is well known that the interatomic interactions can be changed by modulating the s-wave scattering length using the Feshbach resonance[1-8].This offers a good opportunity for manipulation of atomic matter waves and nonlinear excitationsinBECs.Especiallyforaperiodic modulation,it has been applied to control the soliton interaction in BECs[9],the collapse[10]and stabilization[11]of the solitons.Furthermore,the periodic modulationwould induce the resonance of the condensate itself[12-15].

Resonance is an interesting feature of any oscillation under the action of an external periodic field.In physics,resonance is the tendency of a system to oscillate at larger amplitude at some frequencies than at others.When damping is very small,the resonant frequency is approximately equal to the natural frequency of the system,which is the frequency of free vibrations.Recently,the generation of resonances via a periodic variation of the atomic scattering length has been demonstrated in some investigations about BEC[12-15].Scientist often considers the nonlinear problems without damping,starting from the pure Gross-Pitaevskii（GP）equation,and examines the BEC width[12-15]to illustrate the properties of resonance phenomenon.The growth of the BEC width under resonance has been indicated.However, in the realistic system,the BEC is prone to damping due to a small thermal cloud[16-22].This would disturb the resonance.Until now,few investigations have aimed at the resonance of BEC under damping.

In this study,a systematical comparison of the resonance of BEC without damping and that with dampingrevealstheirproperties.Following customary manipulation,we induce the resonance by varying the scattering length periodically.Our results show that the damping mechanism can cause a remarkable change in the resonance.The following is the main difference between the undamped resonant BEC and the damped one:①the damping leads to the narrowing of resonance and the decreasing of the driving frequency,②the BEC width does not increase dramatically under damping when resonance arises,③when the modulation frequency is not far off the most important resonance frequency,the BEC withoutdampingcanabsorbandemitenergy repeatedly,whiletheBECunderdampingis dynamically equilibrated at a lower energy state,④the most remarkable difference comes from the interconversion of energy.In the absence of damping, the energy interconversion under resonance mainly contains the contribution of kinetic energy and potential energy.While in the presence of damping, the resonance arises with the energy interconversion mainly between potential energy and interaction energy.

2 Model and equations

At zero temperature,the dynamics of the BECs is governed by the GP equation：

ψ（x，t）denotes the macroscopic order parameter of the system,VExt（x）the confining potential,m the atomic mass,and g（t）=4πh2a（t）/m the scattering amplitude,where a（t）is the s-wave scattering length. Here,we consider the BEC in a harmonic potential VExt（x）=mω2x2/2,where ω is the frequency of the trap.

As indicated above,we assume the scattering lengthtobetemporallymodulatedsothatthe nonlinear coefficient takes the form：

where h is the amplitude of ac parts,and Ω（Ω＝cω）is the ac-modulation frequency.The modulation can be obtained by temporally varying magnetic field near the Feshbach resonance[9-11,23,24].So the atomic scattering length can be expressed as：

where a∞is the far-off-resonant scattering length,t is the time,B0and Δ are the resonance positionandwidth,respectively.Regarding experimental values of the parameters B0and Δ, Feshbach resonances have been observed in23Na at 853 G and 907 G[4],in7Li at 725 G[25]and in85Rb at 164 G with Δ=11 G[26].

The aim of this study is to demonstrate the influence of damping in BEC when the dynamical resonance arises by varying the scattering length periodically.Generally speaking,the GP model relies on the mean-field description of a boson gas at extremely low temperatures and becomes exact at T= 0.When the temperature is finite,but still much below the critical temperature Tcfor BEC formation, there exists a fraction of atoms that is not condensed, the so-called thermal cloud.This thermal cloud is in fact coupled to the condensed gas and its presence produces effects that are not accounted for by the GPequation.Phenomenologically,oneofthemost noticeableeffectsofthepresenceofasizable thermal cloud is the introduction of damping to the condensed gas.

Theapproachofaddingphenomenological damping to emulate thermal effects was originally proposed by Pitaevskii.Following the custom,we add a damping term h γ ψ/t to the left-hand side of equation（1）[16-22].Then,we get：

Undoubtedly,thedampingwillcausea dissipation of energy from the system.But,the periodical modulation of the scattering length will induce excitations.So,the two mechanisms will compete with each other until a new equilibrium state formed.

3 Initial conditions for the model

In numerical simulation,we take the density profile approximated by the Thomas-Fermi(TF) solution as initial condition, μ is the chemical potential of the atom.For the sake of simplicity,we set h =1,the chemical potential μ=1, the atomic mass m=1,and the scattering amplitude g0=1.Thus the spatial extent of the system is characterized by the healing lengthand the time unit is ξ/c.Meanwhile,we havec/ξ for the external potential.The ac-modulation amplitude h is 0.1g0.

We now estimate the parameters for a realistic experiment.For a23Na condensate with m=38.18× 10-27kg and a∞=2.8 nm[27],we assume the tight transverse confining frequency ω┴=500×2π Hz and the onedimensional peak condensate density n1D=5×107m-1. Thus the longitudinal confining frequency is 66.2× 2π Hz.Our space and time units correspond to 0.56 μm 1.1×10-4s and respectively.The system has the number of atoms N0≈11000.

4 Results

Usually,even small periodic driving forces can produce large amplitude vibrations at the resonant frequencies,because the system stores vibrational energy.Hence,thetemporalmodulationofthe scatteringlengthcanbeviewedasadriving manipulation,which leads to the energy transfer into BEC.The initial condition of the system uses the TF solution which approaches the ground state,so our experiments start from a low energy condensate. Here,the initial energy of the BEC is 24.12μ.The energy of the system is calculated by the function,

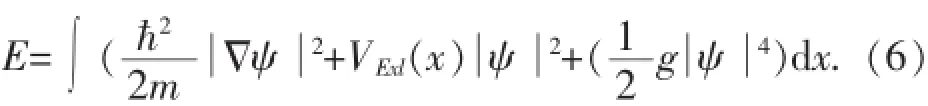
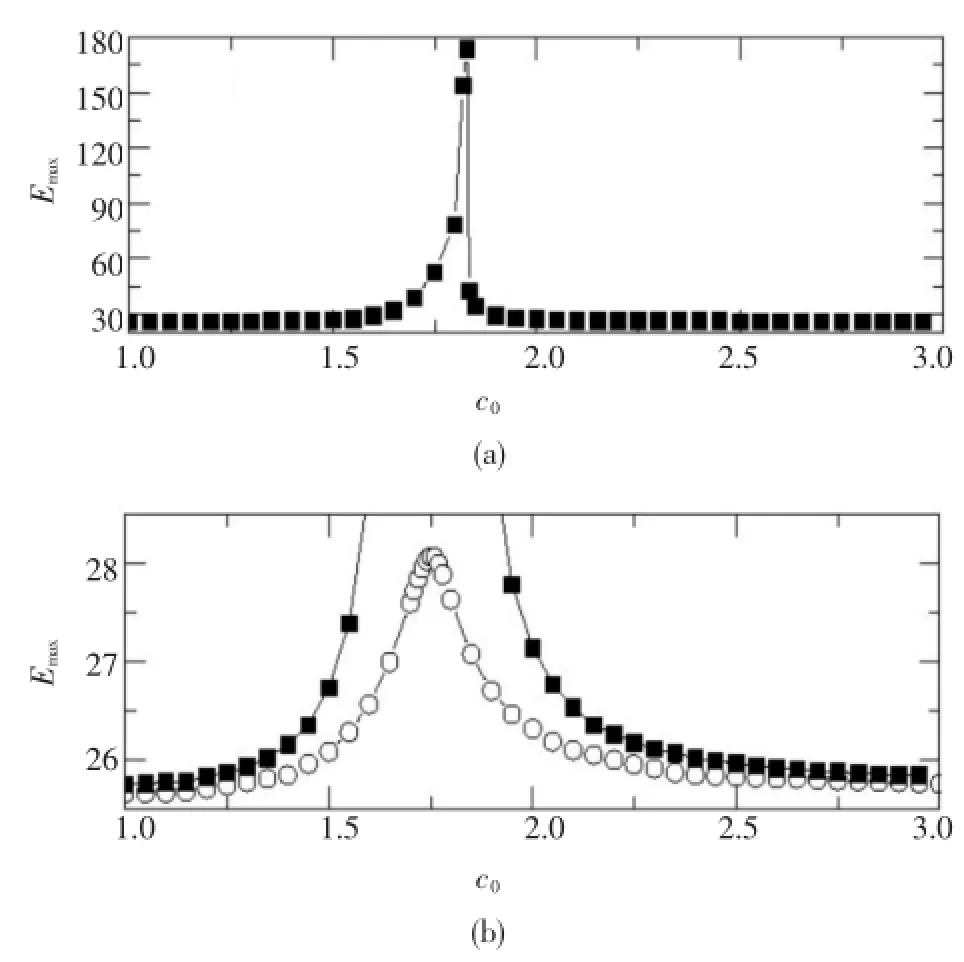
Fig.1 The maximum energy of condensate versus the coefficient c.Note the drive frequency Ω=cω.（a）γ=0（squares）;（b）γ=0（circles）and γ=0（squares）.The amplitude of the driving is h=0.1g0.The energy is in units of μ,and the corresponding unit in the following pictures are the same as in this picture.

We firstly test various drive frequencies to find themostimportantresonancefrequencies.Our investigation is based on the numerical simulation. Fig.1 plots the values of the maximum energy obtained by the periodical modulation.Without damping,we find the maximum energy of the BEC reaches the peak value when the frequency approaches 1.83 ω [see Fig.1（a）].In Ref.[15],Abdullaev and Garnierhaveexploredthefrequencybymeasuringthe oscillation amplitude of the BEC.In Fig.1（b）,we obtain the greatest value at the frequency of 1.75ω when the damping rate is 0.01.Note the damping rate in real system is related to some factors such as the temperature.In lots of investigations,this rate ranges from 0 to 0.03.Here,we choose the value γ=0.01. Comparing the two cases,the damping leads to a narrowing and a decreasing shift of the resonance in the drive frequency.

What does the damping affect the resonance?In above,we have only shown the change of the drive frequency and the maximum energy.It seems to be a quantitativedifferencebetweenthetwocases. Furthermore,we find the most important resonance frequencies:1.75ω and 1.83ω corresponding to the two cases respectively.In the following,we will mainly take the two frequencies to explore the properties of resonance.

In order to further study the resonance of BEC, we calculate the root mean square distance,=which is defined as：

Fig.2 plots the BEC width obtained from the root mean square distance as a function of time. Without damping,Fig.2（a）shows the BEC width is prone to steadily increase at the most resonant response.When the drive frequency is 1.75ω,the oscillation amplitude of the BEC width periodically increases to a maximum and then decay to the original value[see Fig.2（c）].Such a growth and decay cycle of the amplitude keeps on repeating.In the presence of damping,the oscillation amplitude of the BEC width completely degenerates.In Figs.2（b）and 2（d）,the BEC width eventually evolves to a periodic cycle,which differs from that in Figs.2（a）and 2（b）.In fact,the evolution of the BEC width follows the modulation of the scattering length. Furthermore,in Figs.2（b）and 2（d）,we can not determine whether the resonance takes place due to the unremarkable BEC width.This is why we do not specially stress the BEC width in this paper.In the next text,we will essentially confirm that the four instances are in resonance.

Fig.2BECwidthversustimeforthenonlinear management.（a）Ω=1.83ω，γ=0；（b）Ω=1.83ω，γ=0.01；（c）Ω= 1.75ω，γ=0；（d）Ω=1.75ω，γ=0.01；The length unit is ξ=h/,and the time unit is ξ/c.The corresponding units in the following pictures are the same as in this picture.

Fig.3 detailedly show the energy evolution.At themostimportantresonancefrequencywithout damping,energy can be steadily pumped into BEC until the system is equilibrated by the external potential[see Fig.3（a）].In Fig.3（c）,the energy evolution is also periodic,and it just likes the evolution of the oscillation amplitude in Fig.2（c）. Theenergypumpsinandoutofthesystem. Consequently,the resonance of the system has a peculiar nature:the oscillation amplitude gradually passes through pronounced maxima and minima[seeFig.2（c）].In Ref.[14],Adhikari shows a possible explanation.After the amplitude attains a certain value,the external force and the oscillation become out of phase,and the system loses energy in each cycle.Thus,the amplitude of oscillation passes through a maximum and minimum.And the growth and decay cycle of the amplitude keeps on repeating. With damping rate r=0.01,energy evolves fast to a periodic modulation and does not change as that in Fig.3（c）.This indicates the system evolves into a dynamic equilibrium state,which results from the damping and the ac driving and oscillates as the modulation of the scattering length.

Fig.3 Energy evolution of condensate under the nonlinear management.（a）Ω=1.83ω，γ=0；（b）Ω=1.83ω，γ= 0.01；（c）Ω=1.75ω，γ=0；（d）Ω=1.75ω，γ=0.01.

For the usual resonance,such as an oscillator, when it is at maximum displacement,its potential energy is at a maximum as well.From there,it beginsmovingtowardthepositionofstable equilibrium,and as it does so,it loses potential energy and gains kinetic energy.Once it reaches the stable equilibrium position,kinetic energy is at a maximumandpotentialenergyataminimum. WhetherdoesthenonlinearresonanceofBEC display this feature?In above text,even we can obtain some evidence of resonance according to the BEC width and the maximum energy,it is not easy to obtain this feature because the BEC does not behave like the oscillator.

Fig.4（color online）The temporal evolution of kinetic energy（black line）,potential energy（red line）and interaction energy（green line）.（a）Ω=1.83ω，γ=0；（b）Ω= 1.83ω，γ=0.01；（c）Ω=1.75ω，γ=0；（d）Ω=1.75ω，γ=0.01.

Now we aim at the energy interconversion of the resonant BEC.In Fig.4（a）,we can see the oscillation amplitude of kinetic energy and potentialenergyisapproximatelyequal.Meanwhile,the oscillation frequency of kinetic energy and potential energy is almost equal.Consequently,kinetic energy and potential energy convert each other in the resonance process.On value,they form crossovers. Fig.4（c）shows a coupling among kinetic,potential andinteractionenergy.Thisinterconversion corresponds to the energy evolution in Fig.3（c）.In Fig.4（b）and 4（d）,we can see the interconversion mainlyconcentratesonpotentialenergyand interaction energy.On value,they cross each other obviously.In a word,the energy interconversion of BEC in nonlinear resonance is different from that of the oscillator.But the essential interconversion of energy to construct resonance is similar.It is easy to understandthesephenomena.TheBECisa nonlinear system,and its energy comes from not only kineticenergyandpotentialenergy,butalso interaction energy.Hence,energy interconversion in nonlinear resonance of BEC displays various modes.

We now compare Fig.4（a）with（b）and Fig. 4（c）with 4（d）.Although the modulation frequency is the same,the damping compels the interconversion to focus on interaction energy and potential energy. Under damping,the oscillation amplitude of kinetic energy is much smaller than that of potential energy（interaction energy）.And the oscillation frequency of kinetic energy mismatches with that of potential energ（interaction energy）too.Specially,interaction energy and potential energy can form the crossover on value in Fig.4(b)and 4(d).This indicates that the damping weakens the excitation of kinetic energy in resonance.It has the resonance with different energy interconversion degenerate to a fixed mode.

Finally,wementionthefar-off-resonant frequencies.Fig.1 has shown that these frequencies donotinduceahigh-energycondensate. Importantly,the value of potential energy,kinetic energyandinteractionenergydoesnotform crossovers at all when the driving frequencies are far from the most important frequencies(see Fig.5). Furthermore,the oscillation frequencies of potential energy,kinetic energy and interaction energy tend to be disordered.These properties indicate that the BEC indeed does not undergo resonance.In reverse, Fig.4 completely indicates that the BEC is in resonance.

Fig.5（color online）The temporal evolution of kinetic energy（black line）,potential energy（red line）and interaction energy（green line）as the drive frequency is faroff-resonant frequency.（a）Ω=1.2ω，γ=0；（b）Ω=1.2ω，γ=0.01.

The resonance of BEC under damping is firstly considered.Due to the interatomic interaction,the resonance of BEC can arise with various modes of the energy interconversion.Our investigation mainly showsthedifferencebetweenresonancewithout damping and that with damping.In fact,resonance is also dependent on other factors such as the trapping potential,thestrengthofinteractionandthe amplitudeoftheacmodulation.Differingfrom previous works[12-15],we concentrate on the energy of thesystem.Althoughthisworkpreliminarily illustrates the formation of the resonance of BEC,it has clearly demonstrated the properties.Furthermore, the damping rate can also control resonance.If the damp rate is very small(approaches zero),resonance with damping will act as that without damping. Certainly,if the damping rate is very big,the BEC would not form resonance at all.

5Conclusion

By numerically solving the corresponding GP equation,wehavesystematicallystudiedtheresonance of BEC both with and without damping. Our results have shown some difference between the twocases,includingthemostimportantdrive frequencies,the BEC width,the transfer of energy and the energy interconversion.The crossover of kinetic energy,potential energy or interaction energy on value can indicate the BEC is in resonance.In the absence of damping,kinetic energy can be intensively excited as resonance occurs,whereas in the present of damping,a driven system with lower energy state appears,and the energy interconversion mainly focuses on potential energy and interaction energy.Therefore,dampingnotonlycausesa quantitative difference in the resonant frequency and amplitude,but also completely changes the energy interconversion in resonance.

[1]Moerdijk A J,Verhaar B J,Axelsson A.Resonances in ultracold collisions of6Li,7Li,and23Na[J].Phys.Rev.A,1995,51(6):4852-4861.

[2]Roberts J L,Claussen N R,James P Burke,et al.Resonant magnetic field control of elastic scattering in cold85Rb[J].Phys.Rev. Lett.,1998,81(23):5109-5112.

[3]Stenger J,Inouye S,Andrews M R,et al.Strongly enhanced inelastic collisions in a Bose-Einstein condensate near feshbach resonances[J].Phys.Rev.Lett.,1999,82(12):2422-2425.

[4]Inouye S,Andrews M R,Stenger J,et al.Observation of Feshbach resonances in a Bose–Einstein condensate[J].Nature,1998,392 (6672):151-154.

[5]Cornish S L,Claussen N R,Roberts J L,et al.Stable85Rb Bose-Einstein condensates with widely tunable interactions[J].Phys.Rev. Lett.,2000,85(9):1795-1798.

[6]Donley E A,Claussen N R,Cornish S L,et al.Dynamics of collapsing and exploding Bose-Einstein condensates[J].Nature,2001, 412(6844):295-299.

[7]Regal C A,Jin D S.Measurement of positive and negative scattering lengths in a Fermi gas of atoms[J].Phys.Rev.Lett., 2003,90(23):230404.

[8]Volz T,Dürr S,Ernst S,et al.Characterization of elastic scattering near a Feshbach resonance in87Rb[J].Phys.Rev.A,2003,68(1): 010702.

[9]Zhang X F,Yang Q,Zhang J F,et al.Controlling soliton interactions in Bose-Einstein condensates by synchronizing the Feshbach resonance and harmonic trap[J].Phys.Rev.A,2008,77 (2):023613.

[10]Abdullaev F K,Caputo J G,Kraenkel R A,et al.Controlling collapse in Bose-Einstein condensates by temporal modulation of the scattering length[J].Phys.Rev.A,2003,67(1):013605.

[11]Adhikari S K.Stabilization of bright solitons and vortex solitons in a trapless t hree-dimensional Bose-Einstein condensate by temporal modulation of the scattering length[J].Phys.Rev.A,2004, 69(6):063613.

[12]Rajendran S,Muruganandam P,Lakshmanan M.Nonstationary excitations in Bose–Einstein condensates under the action of periodicallyvaryingscatteringlengthwithtimedependent frequencies[J].Physica D,2007,227(1):1-7.

[13]Abdullaev F Kh,Galimzyanov R M,Brtka M,et al.Resonances in a trapped 3D Bose–Einstein condensate under periodically varying atomic scattering length[J].J.Phys.B:At.Mol.Opt. Phys.,2004,37(17):3535-3350.

[14]Adhikari S K.Resonance in Bose–Einstein condensate oscillation from a periodic variation in scattering length[J].J. Phys.B:At.Mol.Opt.Phys.2003,36(6):1109-1120.

[15]Abdullaev F K,Garnier J.Collective oscillations of onedimensional Bose-Einstein gas in a time-varying trap potential and atomic scattering length[J].Phys.Rev.A,2004,70(5):053604.

[16]Choi S,Morgan S A,Burnett K.Phenomenological damping in trapped atomic Bose-Einstein condensates[J].Phys.Rev.A, 1998,57(5):4057-4060.

[17]Jin D S,Matthews M R,Ensher J R,et al.Temperaturedependent damping and frequency shifts in collective excitations of a dilute Bose-Einstein condensate[J].Phys.Rev.Lett.,1997, 78(5):764-767.

[18]MertesKM,MerrillJW,Carretero-GonzálezR,etal.Nonequilibrium dynamics and superfluid ring excitations in binary Bose-Einstein condensates[J].Phys.Rev.Lett.,2007,99(19):190402.

[19]Liu C F,Tang Y.Metastable state and macroscopic quantum tunneling of binary mixtures[J].Eur.Phys.J.B,2009,70(2):193-199.

[20]Liu C F,Fan H,Zhang Y C,et al.Circular-hyperbolic skyrmion in rotating pseudo-spin-1/2 Bose-Einstein condensates with spin-orbit coupling[J].Phys.Rev.A,2012,86(5):053616.

[21]Liu C F,Liu W M.Spin-orbit-coupling-induced half-Skyrmion excitations in rotating and rapidly quenched spin-1 Bose-Einstein condensates[J].Phys.Rev.A,2012,86(3):033602.

[22]Liu C F,Hu K,Hu T,et al.Tunneling of a Bose-Einstein condensate under damping[J].Journal of Low Temperature Physics, 2010,160(1-2):32-40.

[23]Staliunas K,Longhi S,Valcácel G J de.Faraday patterns in Bose-Einstein condensates[J].Phys.Rev.Lett.,2002,89(21):210406.

[24]Saito H,Ueda M.Dynamically stabilized bright solitons in a twodimensional Bose-Einstein condensate[J].Phys.Rev.Lett.,2003, 90(4):040403.

[25]Strecker K E,Partridge G B,Truscott A G,et al.Formation and propagation of matter-wave soliton trains[J].Nature,2002,417 (6885):150-153.

[26]Courteille P,Freeland R S,Heinzen D J,et al.Observation of a Feshbach Resonance in cold atom scattering[J].Phys.Rev.Lett., 1998,81(1):69-72.

[27]Samuelis C,Tiesinga E,Laue T,et al.Cold atomic collisions studied by molecular spectroscopy[J].Phys.Rev.A,2000,63(1): 012710.

2012-12-17

国家自然科学基金项目（11247206）；江西省教育厅基金项目（GJJ13382）

刘超飞（1981-），男，博士，讲师，主要从事玻色爱因斯坦凝聚等方面的研究，E-mail:liuchaofei0809@163.com.