基于博弈论的启发式搜索算法的改进研究

汪孔斌 尹弼民

(铜陵职业技术学院，安徽铜陵244000；南昌大学软件学院，江西南昌330047)

基于博弈论的启发式搜索算法的改进研究

汪孔斌 尹弼民

(铜陵职业技术学院，安徽铜陵244000；南昌大学软件学院，江西南昌330047)

基于博弈理论提出了一种路径搜索问题的优化算法。将路径搜索问题的搜索空间映射为博弈的策略组合空间，而路径搜索问题的目标函数映射为博弈的效用函数，通过遍历博弈支持集搜索纳什均衡解，并利用启发思想根据博弈的结构制定搜索策略，以期望用最小的代价减少搜索节点数、提高应用系统的性能及效率。

路径搜索；启发式；博弈论；纳什均衡

1.引言

搜索技术是人工智能的一个重要研究内容，路径搜索是地理信息系统、导航系统、无线传感网络[1]以及计算机网络等系统中的一个典型应用，通常需要考虑以下几个因素：一，路径搜索频繁；二，网络规模庞大，节点数量多；三，需要近乎实时的响应速度。如果系统是应用在移动设备上，还需要考虑设备的硬件资源(运算、存储等)有限等因素。

搜索算法可以分为盲目搜索算法和启发式搜索算法，二者的区别在于，启发式搜索算法的每一步都试图向着目标状态方向进行搜索[1]，而盲目搜索算法的每一步按固定之规则而搜索，然后判断是否达到目标状态。因而，启发式搜索算法克服了盲目搜索算法的盲目性问题。

本文以经济学博弈论为基础，提出一种改进的启发式搜索算法，新算法的基本思路是将问题的搜索空间映射为博弈的策略组合空间[6]，目标函数映射为博弈的效用函数，通过遍历博弈支持集搜索纳什均衡解，并利用启发思想根据博弈的结构制定搜索策略，以期望用最小的代价减少搜索节点数、提高应用系统的性能及效率。

最后，在Android平台上实现其仿真实验，并将其与深度优先搜索算法、广度优先搜索算法，Dijkstra算法，最佳优先(best-first search，BFS)搜索算法、Dijkstra A*算法（一种基于Dijkstra的启发式算法）的仿真结果进行比对，以实例数据验证了该算法的灵活性、有效性以及平衡最优性。

2.改进博弈算法

定义1设x为路径搜索问题中的变量，f为问题中待解目标函数，博弈结构G=[I,S,U]，称映射Φ：x-＞s为一个决策变换。映射Ψ：f-＞U为一个效用变换。

定义2从某个局势s开始，所有主体顺序选择(在本文中，博弈主体进行局势演化的先后顺序依照当前所选择的节点到目标点的直线物理距离的升序排列)各自最优反应的动态过程称为一个回合。

关于定义1的两个变换，将问题寻找最短路径的过程变换为博弈主体寻求结构G的最优均衡点的演化过程。记改进博弈算法AGA（Advanced Game Algorithm）为一个五元组：

公式注解：

结构G：对于x的每一个分量xi∈{0,1}，用1个博弈主体的策略表示，即为I={1，2，...，n}；n个博弈主体的策略组合s即对应于路径搜索问题中选择的一条路径；而同一策略组合之下各主体的效用相等：若s是可行解，ui（s）=f（s），否则回溯到上一步。

初始局势s0：每个主体从自己的策略空间中随机地选择一个策略构成初始局势s0，这是主体进行博弈演化的起点。

主体行为算子α：假设参与博弈的主体追求自身效用最大化，则主体行为算子α即为主体在演化局势中的最优反应对应，最优反应对应通过比较该主体所有可能策略在该局势下的效用求得。

局势演化算子ζ：各主体通过顺序最优反应动态达到的纳什均衡并不一定是帕累托最优的，于是使用局势演化算子?对均衡状态施加随机扰动，使之偏离原均衡状态，接着由各主体的顺序最优反应动态恢复到新的均衡状态。不断重复这样的扰动恢复过程直至搜寻到更优的均衡状态。对于s的第i个分量，即主体i的所取策略s(i)，若均匀随机数rand (0,1)小于扰动概率p(实验中设定p=0.1)，则用主体i当前策略的相反策略替换当前策略；否则维持原策略不变。对s的所有分量重复这样的选择方式即得扰动后的局势s’.

停止准则τ：称达到均衡的两个回合博弈称为博弈演化的一代.本文的停止准则取为τ＞T,T为预设的演化最大代数。事实上，T越大，所得到的结果越接近最优解（或就是最优解），但是同时消耗的时间也越多。

关于定义2，经过作用主体行为算子的两个回合，局势演化序列必定达到纳什均衡状态。这是因为第一个回合后达到的策略组合必是可行解，第二个回合后达到的策略组合必是均衡状态。因为非可行解的效用总是小于可行解的效用，而第二个回合的开始局势是可行解，所以第二个回合历经的状态都是可行解，由反证法可以得到第二回合后到达的策略组为均衡状态，具体参考文献[6]中的证明。

3.算法分析

首先开发出启发因子TempEdge类，该类为现时准备走的边，包括边的开始节点和目的节点，为优先队列设置比较器。对所有边的目的节点按照其到target的直线直线物理距离进行排序，产生List＜TempEdge＞edges队列，然后在void AGA()算法中实现路径选择。注意设置局势演化算子，使用线程实现每隔3000ms自动演化一次，设置停止准则T，并针对不同大小的T值进行实验，记录数据。摘取两段代码如下：

算法1.比较器中重载的比较函数.

@Override

public intcompare(TempEdge o1,TempEdge o2){

//TODO Auto-generatedmethod stub

int[]target=game.target;

//直线物理距离

int a=(o1.gettEnd0()-target[0])*(o1.gettEnd0()-target[0])+(o1.gettEnd1()-target[1])*(o1.gettEnd1()-target[1]);

int b=(o2.gettEnd0()-target[0])*(o2.gettEnd0()-target[0])+(o2.gettEnd1()-target[1])*(o2.gettEnd1()-target[1]);

return a-b;

}

算法2.AGA算法（截取一段）.

double pmark=Math.random();

if(pmark＜P){//P为局势演化算子，此时发生随机扰动

Random r=new Random();

inth=r.nextInt(edges.size());

currentEdge[0][0]=edges.get(h).gettStart0();

currentEdge[0][1]=edges.get(h).gettStart1();

currentEdge[1][0]=edges.get(h).gettEnd0();

currentEdge[1][1]=edges.get(h).gettEnd1();

//取出此边的目的点

tempTarget[0]=currentEdge[1][0];

tempTarget[1]=currentEdge[1][1];

edges.remove(h);}

else{//当随机数大于P时，随机扰动不发生，

//直接取出优先队列中第一个数字即可

currentEdge[0][0]=edges.get(0).gettStart0();

currentEdge[0][1]=edges.get(0).gettStart1();

currentEdge[1][0]=edges.get(0).gettEnd0();

currentEdge[1][1]=edges.get(0).gettEnd1();

//取出此边的目的点

tempTarget[0]=currentEdge[1][0];

tempTarget[1]=currentEdge[1][1];

edges.remove(0);

}

本文算法在Android平台上的仿真结果截图如下：

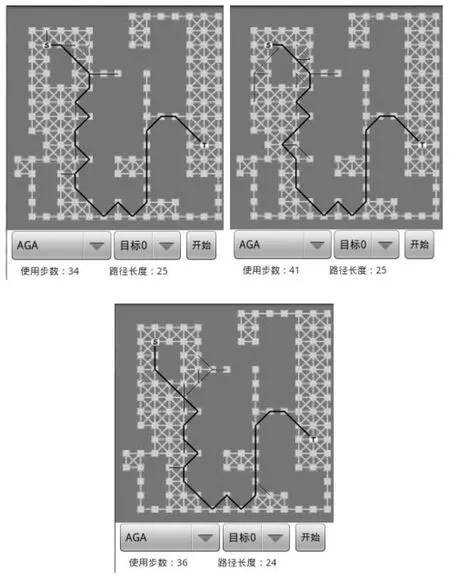
图3-1 AGA算法搜索目标0的三张例图

图3-2 AGA算法停止后目标0的路径解

4.实验对比

深度优先搜索算法是把最近刚产生的结点优先扩展，直到达到一定的深度限制。若未找到目标或无法再扩展时，再回溯到另一个结点继续扩展[2]。

广度优先搜索算法（Breadth-First-Search），是一种图形搜索算法。简单的说，它的基本思路是站在一个节点上，先将所有连接到该节点的节点访问到，再继续访问下一层，直到找到目标为止。广度优先搜索算法具有完全性。即无论图形的种类如何，只要目标存在，则它一定会找到。

Dijkstra算法其基本原理是：每次新扩展一个距离最短的点，更新与其相邻点的距离。当所有边权均为正时，由于不会存在一个距离更短的没扩展过的点，故这个点的距离永不会再被改变，从而保证算法的正确性。不过依据此原理，用Dijkstra求最短路的图不能有负权边，因为扩展到负权边时会产生更短的距离，有可能会破坏已经更新的点距离不会改变的性质[3]。

本例中最佳优先搜索算法是对广度优先算法的一种优化，它的思想为：在所有可能达到的下一个节点中选择与目的节点最接近的节点。

对Dijkstra算法的优化同样类似，建构的是一种基于Dijkstra的启发式寻径方法，在被优化的算法中，针对最短距离和现下距离作了一次比较，从而改进原有算法。如此，则为本例中的Dijkstra A*算法[3]。

算法的仿真结果比对如后表所示：

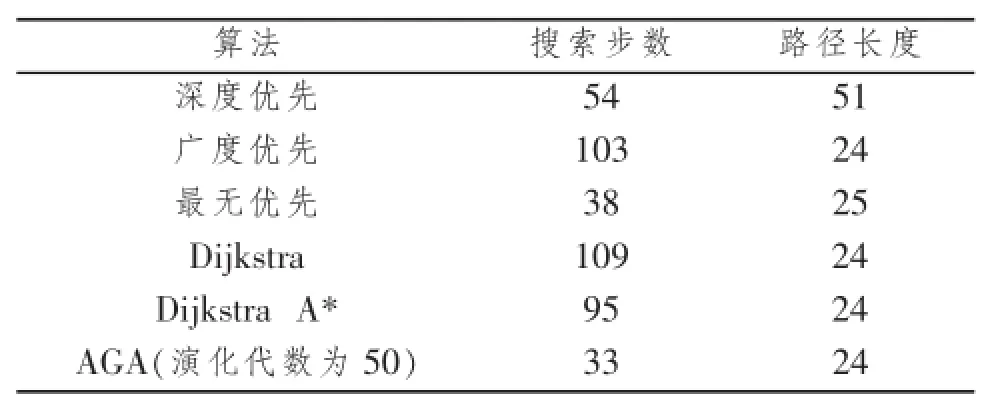
表1 目标0之实验结果比对

表2 目标1之实验结果比对

5.结论

经过仿真实验的对比，表明这种基于博弈论的改进启发式路径搜索算法相较传统的搜索算法而言，可以避免重复无效的搜索，提高搜索效率，同时能够尽可能地搜索出问题优解，并且在应用方面，有着灵活性、有效性以及平衡最优性。

[1]米志超，周建江，邵海林.一种启发式能量优化的无线传感器网络数据收集算法[J].武汉大学学报(理学版)，2008，（3）：338-342.

[2]龚建华.深度优先搜索算法及其改进[J].现代电子技术，2007，（22）：90-92.

[3]王景存，张晓彤，陈彬，陈和平.一种基于Dijkstra算法的启发式最优路径搜索算法[J].北京科技大学学报，2007，（3）：346-350.

[4]周阳，樊建华，王志芹，张洁华.基于节点度和最小支撑聚类的路径搜索算法[J].计算机工程与应用，2013，（9）：164-167.

[5]孙泽宇,姬晓辉.改进启发式蚁群算法求解电网规划优化问题[J].计算机仿真，2013，（1）：183-187.

[6]叶俊，刘贤德，韩露.基于博弈论的背包问题优化算法[J].华中科技大学学报(自然科学版)，2003，（9）：53-55.

[7]王志勇，韩旭，许维胜，杨继君.基于改进蚁群算法的纳什均衡求解[J].计算机工程，2010，（14）：166-168，171.

[8]隗立涛，修乃华.基于启发搜索算法的纳什均衡计算[J].北京交通大学学报，2007，（3）：58-62.

[9]黎萍，杨宜民.基于博弈论的多机器人系统任务分配算法[J].计算机应用研究，2013，（2）：392-395.

（责任编辑：孟伟东）

TP18

：A

：1671-752X（2013）04-0069-03

2013-07-13

汪孔斌（1970-），男，安徽桐城人，铜陵职业技术学院信息工程系实验师；尹弼民（1992-），女，安徽桐城人，南昌大学软件学院在读硕士研究生。