带附加供料流的准理想级联的优化

谢全新 杨 坤 周永胜 牟 宏

（核工业理化工程研究院 天津 300180）

带附加供料流的准理想级联的优化

谢全新 杨 坤 周永胜 牟 宏

（核工业理化工程研究院 天津 300180）

某些同位素分离任务(比如回收铀的浓缩、轻杂质的净化等)需要借助带附加供料流的级联来完成。这类级联的设计目标之一是针对已知的目标组分的精料和贫料丰度，确定级联的结构参数，即确定级联总级数、主供料级以及附加供料级位置。为对该类级联进行理论设计，建立了准理想级联的数学优化模型。优化问题的目标函数为级联中总的物质流量，通过罚函数法把约束条件下的多变量优化问题转化为无约束优化问题，并用单纯形法对后者进行求解。利用该优化方法对浓缩回收铀的级联进行了计算。

准理想级联，附加流，优化，罚函数，回收铀

大分离系数情况下的多组分同位素分离级联的设计和优化通常以准理想级联为模型[1–6]。先通过理论计算设计出符合要求的准理想级联，然后使实际级联的结构尽可能靠近准理想级联。关于准理想级联的计算，有一类典型问题是：已知目标组分(目标同位素)精料和贫料丰度，确定级联的结构，即确定级联的总级数和供料级位置。对于准理想级联，精料和贫料组分丰度分别与级联总级数和供料级位置两个参量之间存在解析关系式。所以对于普通的准理想级联，即只有一股供料流、一股精料流和一股贫料流的级联，在目标组分的精料丰度和贫料丰度已知的情况下，根据它们与级联总级数和供料级位置之间的解析关系式，通过解非线性方程组可以求出级联总级数和供料级位置两个参量，进而确定级联结构[3–5]。然而，某些特殊的同位素分离任务需要借助带附加供料流的级联来完成，比如乏燃料中回收铀的再浓缩[7–9]、原料昂贵的同位素混合物分离后贫料的再利用，以及某些分离过程对轻杂质的净化等[10]。在带附加流的准理想级联模型中，精料和贫料组分丰度与级联总级数、主供料级位置、附加供料级位置间也同样存在解析关系式。但是在已知目标组分精料丰度和贫料丰度情况下，只能建立两个非线性方程，却需确定三个未知量，即级联总级数、主供料级位置、附加供料级位置。因此，通过直接解非线性方程组的方法不能确定这三个未知量，需要借助其它计算方法来确定。本文以级联中总物质流量为目标函数，以级联总级数、主供料级位置、附加供料级位置为优化参量，将带附加供料流的准理想级联的求解问题转化为多变量优化问题，通过用单纯形法对其求解，最终确定三个未知参量，进而确定级联其它参量。

1 数学模型及基本概念

本文研究的带附加流的准理想级联是如图1所示的逆流型级联，级联具有主供料流F、附加供料流E、精料流P和贫料流W，相应的组分丰度分别为iFC、iEC、iPC、iWC(mi,...,1=，m为待分离同位素混合物的组分数)。级联共有N级，第f级为主供料级，第l级为附加供料级。

图1 带附加供料流的逆流型准理想级联Fig.1 Countercurrent quasi-cascade with an additional feed flow.

上述各级联参量之间存在以下解析关系[11]：

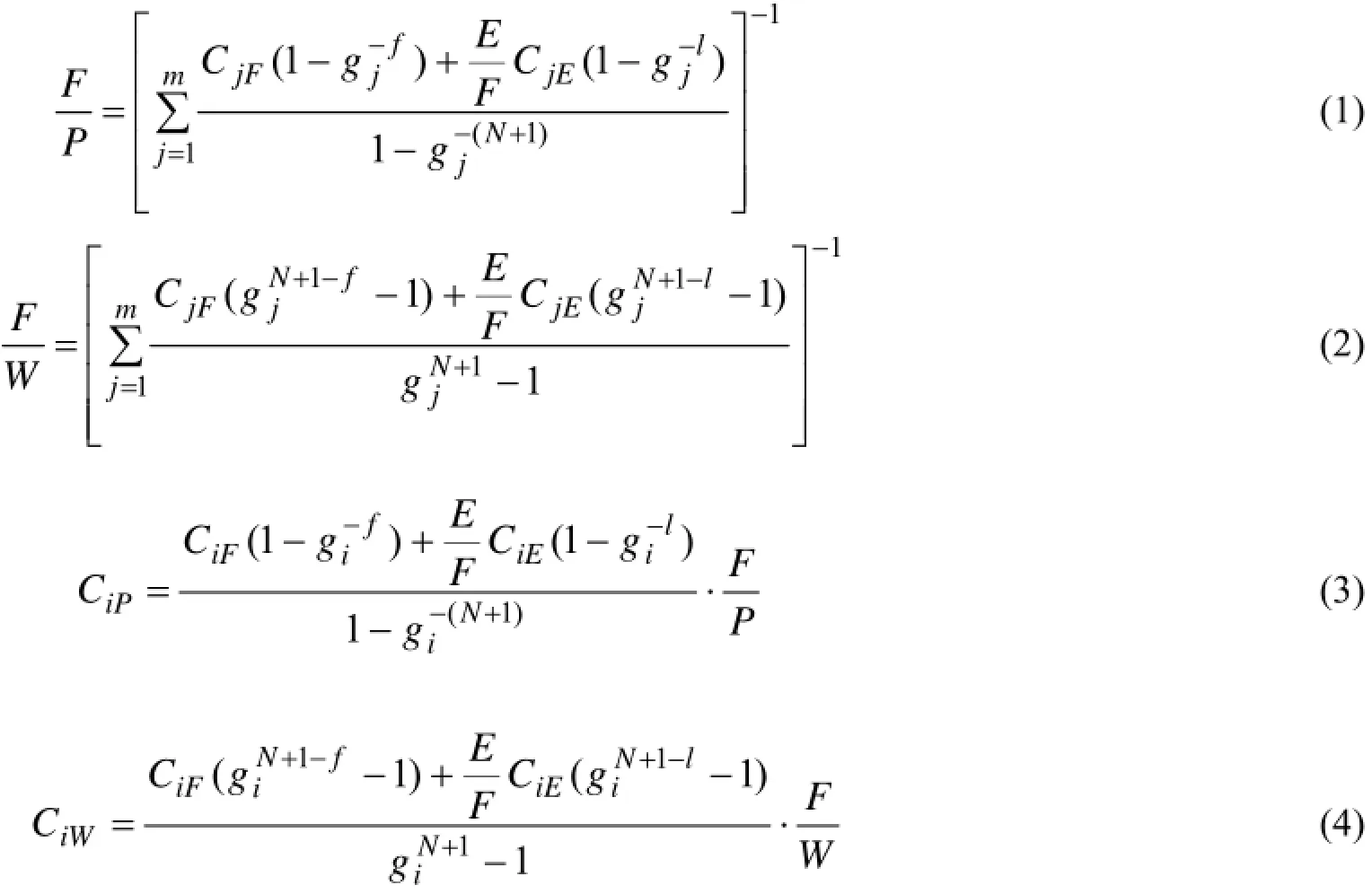
级联中相对总物质流RL(总物质流TL与级联精料流P之比)由下式确定：

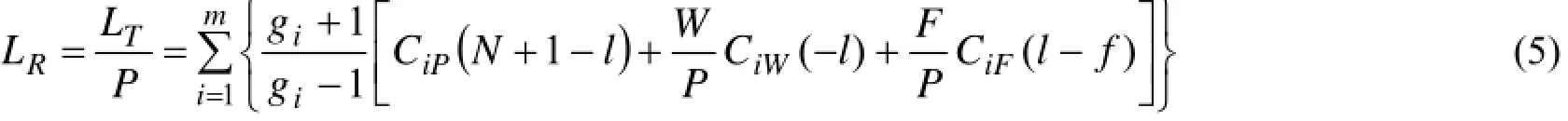
式(1)–(5)中的ig为第i组分的精料流与贫料流"iL之比，即：

对于准理想级联，gi为常量，并可表示为[4,6,11]：

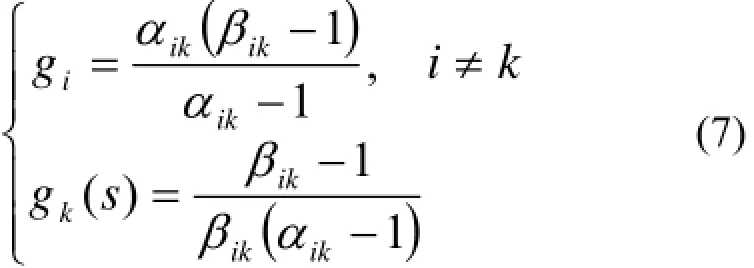
式中，k是关键同位素的组分序数；αik、βικ是第i、k 两种组分的精料相对分离系数与贫料相对分离系数，准理想级联的αik、βικ各级相等。

由式(7)可以得到：

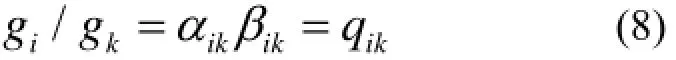
式中，ikq是第i、k两种组分的相对全分离系数。对于大多数基于分子动力学的分离方法，相对全分离系数ikq可表示为[4,5,11–15]：

式中，q0为基本全分离系数。

对于丰度比匹配级联(简称M级联或MARC)，gi可以用基本全分离系数q0以及组分摩尔质量来表达[2–5,11–14,16,17]：

其中：

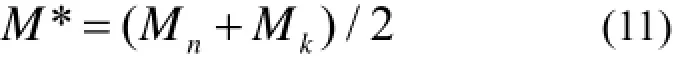
式中，Mn和Mk为第n和第k组分的摩尔质量。

带附加供料流的级联计算跟普通级联的计算一样，可以分成两种类型。一类是级联结构已经确定即级联总级数N、主供料级f、附加供料级l以及gi值已知。在给定供料丰度CiF、CiE以及两供料流的比值E/F条件下，根据式(3)、(4)求精料组分丰度CiP与贫料组分丰度CiW，再根据式(5)求级联中的总物质流量LT。这类计算即验证实际级联的运行结果是否与理论计算相符。另一类计算是级联的设计计算，该类计算最典型问题为：已知目标组分的精料丰度、贫料丰度确定级联结构，即确定级联总级数N、主供料级f以及附加供料级l。在这种情况下可以建立两个方程，即在i=n情况下的式(3)、(4)，式左边为已知量和，右边的参量CiF、CiE、gi、E/F一般人为给定，这样，式的右边含有三个未知量N、f和l，要确定这三个未知量，还需要一个条件。在多组分同位素分离级联理论中，通常把总物质流量最小的级联称为最佳级联。为求解N、f和l，可以加入级联中总物质流量最小这一条件，即式(5)的LR或LT最小。这样问题转变为以LR或LT为目标函数，以N、f和l为优化变量，以为约束条件的多变量优化问题。

2 级联优化问题的数学表述及其求解方法

优化目标函数取级联中的相对总物质流量LR，优化变量为N、f和l，且1≤f≤N。在优化过程中假设N、f和l为实型变量，在实际应用中再取整，同时令：

式中，T表示转置。则优化问题可表述为如下形式：

式中，hj和λj分别表示等式与不等式约束条件；R是实数域。式(13)是一个约束条件下的多变量优化问题，包括两个等式和三个不等式约束条件。求解约束条件下的最优化问题，有两类方法：一类是利用约束问题本身的性质直接求解，另一类方法是将约束问题转化为一系列无约束最优化问题，以得到约束问题的最优解，通常称之为序列无约束优化方法(Sequential unconstrained minimization technique)，本文将利用后一种方法来求解。约束最优化问题向无约束最优化问题的转化可以通过罚函数法或乘子法等方法来实现。在罚函数法中，将约束函数以一定的方式加到目标函数中去形成罚函数。然后，求这个无约束目标函数的极小。在这种方法中，约束项在无约束优化问题的求解中会使企图违反约束的那些迭代点受到很大的惩罚，即给予其很大的目标函数值，从而迫使一系列无约束问题的极小点收敛到原有约束优化问题的解点。利用外罚函数法(Exterior penalty function method)可将约束优化问题式(13)转化为无约束优化问题[18,19]：式中，Q(X,at,bt)是罚函数；at和bt为正实数，称为罚系数，它取序列值，对于每一个固定的t，at和bt为定值。对于等式约束hj(X)，当hj(X)=0时，不受罚；而当hj(X)≠0时，函数受罚于athj2(X)。对于不等式约束λj(X)，当满足约束条件λj(X)≤0时，项为零；而当违反约束，即λj(X)＞0时，函数受罚于bt[gi(X)]2。

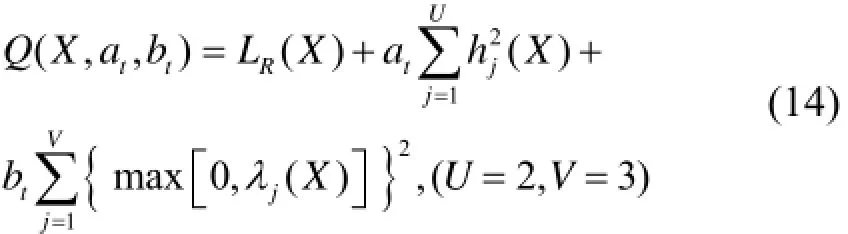
无约束问题式(14)的求解使用单纯形法(Simplex method)[19]，其基本思想是对K个变量，在K维空间中形成K+1个顶点的多面体，然后比较各个顶点的函数值，去掉其中的最坏点代之以新点，形成一个新的单纯形，逐步逼近极小点。

3 理论应用

基于上面的优化方法编写了计算程序，并对浓缩轻水堆乏燃料中回收铀的级联进行了优化计算。回收铀的浓缩不同于天然铀，主要是因为铀核燃料在燃烧的过程中会产生核素232U，而232U及其衰变产物具有γ辐射性[20–22]。因此，在回收铀返回到反应堆之前，必须对232U进行净化，或者把其稀释到允许的丰度值。回收铀经浓缩后，产品中232U与235U丰度比一般不能高于1.1×10–7[23]，即：

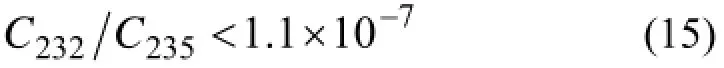
在文献[7,8,11]中用准理想级联理论对俄罗斯轻水堆VVER-440乏燃料后处理之后的回收铀的浓缩问题进行了探讨。提出了不同的级联方案，论证了带附加供料流的准理想级联方案，即天然铀作基本供料，回收铀作附加供料的方案为最佳方案。本文将利用上面所述的优化方法对这种级联进行优化计算。

选UF6为分离工质，天然铀作主供料，其流量为F，组分丰度为CiF。回收铀作附加供料，其流量为E，组分丰度为CiE[8]。天然铀和回收铀各组分的摩尔质量及其丰度列于表1，其中回收铀的组分丰度为轻水反应堆VVER-440的堆后料经10年储存期后的典型丰度。表1中以及本文后面所涉及的组分丰度都为质量丰度。

计算时基本全分离系数取q0=1.0627，式(9)中的n=3、k=5，在这种情况下，235UF6和238UF6两种组分的相对全分离系数1.2。假设235UF6的精料丰度，贫料丰度C3*W=0.2%。针对回收铀中不同的235UF6丰度C3E以及回收铀供料流量E与天然铀供料流量F之比E/F，对级联进行了优化计算，结果如图2所示。

表1 天然铀和回收铀中各组分的摩尔质量及其丰度Table1 Component molar masses and component abundances in the native and recycled uranium.

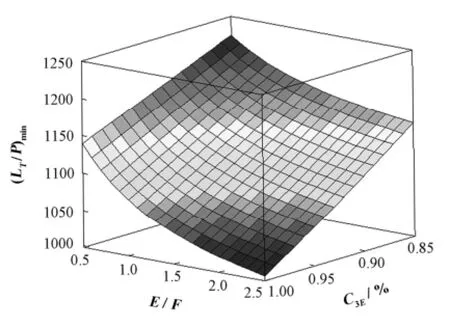
图2 相对流量(LT /P)min与回收铀中目标组分的供料丰度C3E以及E /F的关系Fig.2 Dependence of relative flows (LT /P)min on the abundance of desired component in the recycled uranium C3E and the ratio E /F.

图2 中(LT/P)min表示满足丰度要求(=3.5%，=0.2%)的最佳级联中的总相对物质流量，最佳级联即流量最小的级联。最佳级联的相关参数(如总级数N、天然铀供料位置f、回收铀供料位置l)由约束问题的最优解X*给出。从图2可以看出，(LT/P)min随235UF6供料丰度C3E以及E/F的增加而减少。前者是因为C3E增加，相当于增加目标组分的供料丰度。由于目标组分的精料丰度和贫料丰度是确定的，目标组分供料丰度的增加意味着获得满足丰度要求的产品所需的分离功降低，因此所需的分离器总量也随之减少，这样级联总的物质流量也将减少。当E/F增加时，由于回收铀中目标组分的丰度C3E高于其在天然铀中的丰度C3F，因此E/F的增加也相当于增加了整个级联中目标组分的供料丰度，毫无疑问也将导致级联总的物质流量降低。

当回收铀中目标组分的供料丰度C3E一定的情况下，尽量提高回收铀与天然铀的供料流之比E/F，可以节省分离功。但是E/F的值受限于丰度约束条件式(13)。对于某一回收铀中目标组分的供料丰度C3E，存在一个E/F的极限值(E/F)max。当E/F的值超过该极限值时，丰度约束条件(13)将不再满足。图3列出了不同C3E值之下E/F的极限值(E/F)max， (E/F)max随C3E的增加而增加。当C3E=0.85%时，(E/F)max=2.6；当C3E=1%时，(E/F)max=10。

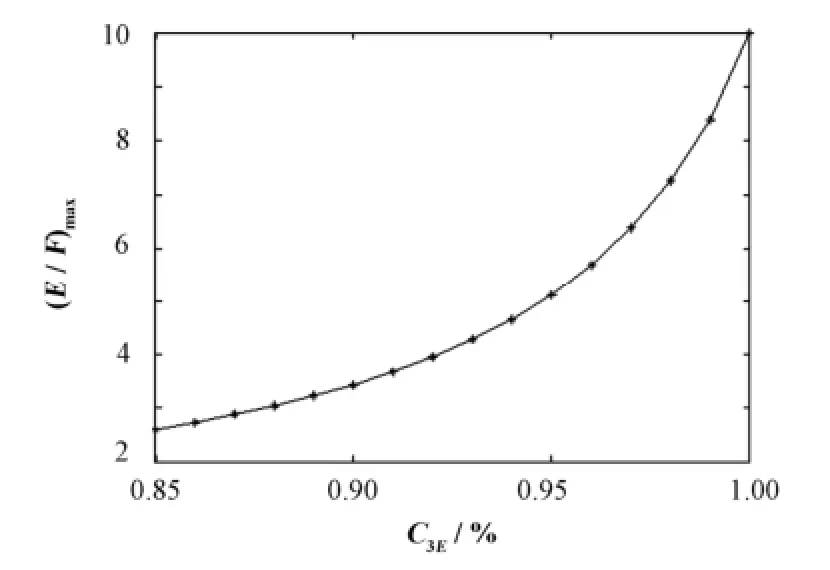
图3 极限值(E/F)max与回收铀中目标组分的供料丰度C3E的关系Fig.3 Dependence of the limited value (E/F)max on the feed abundance of desired component in the recycled uranium C3E.

4 结语

建立了带附加供料的准理想级联优化计算的数学模型，该模型以级联中相对总物质流量作为优化问题的目标函数，以决定级联流量分布的参量M*、级联总级数、主供料以及附加供料位置三个变量为优化参量，并把整实型混合优化问题简化为实型优化问题，利用单纯形法对优化问题进行了求解。

基于所建立的数学模型，用单纯形法对浓缩回收铀的级联进行了优化计算，计算结果表明，级联总物质流量的最小值随回收铀中235UF6的丰度C3E以及附加供料与主供料流之比(E/F)的增加而减少。此外，对于某一回收铀中的目标组分的供料丰度C3E，存在一个(E/F)的极限值(E/F)max，当(E/F)的值超过该极限值时，232UF6与235UF6两组分之间的丰度约束条件将不再满足。

1 Baranov V Y. Isotopes: Properties, Production, Application[M]. Мoscow, IzDAT, 2000: 72–107

2 Xie Q X, Sulaberidze G A, Borisevich V D. Some properties of quasi-ideal cascades with losses at stages[C]. Proceedings of the XX international symposium on physoco-chemical methods of the mixtures separation,“Ars Separatoria 2005”, Szklarska Poreba, Poland, 2005: 205–207

3 Xie Q X, Sulaberidze G A, Borisevich V D. Optimization of model cascades for multicomponent isotope mixtures[C]. Proceedings of XI all-Russia (International) scientific conference, “physical and chemical processes on selection of atoms and molecules”, 2006: 15–20

4 谢全新, 李大勇, 李文泊, 等. 多组分同位素分离级联的优化[J]. 核科学与工程, 2008, (1): 86–91

XIE Quanxin, LI Dayong, LI Wenbo, et al. Cascade optimization for multicomponent isotope separation[J]. Chinese Journal of Nuclear Science and Engineering, 2008, (1): 86–91

5 谢全新, Sulaberidze G A, 吴建军, 等. 存在损耗的多组分级联的改进模型[J]. 原子能科学技术, 2009, 43(8): 750–755

XIE Quanxin, Sulaberidze G A, WU Jianjun, et al. An improved model of multicomponent cascade with losses[J]. Atomic Energy Science and Technology, 2009, 43(8): 750–755

6 Sulaberidze G A, Xie Q X, Borisevich V D. On some properties of quasi-ideal cascades with losses at stages[J]. Ars Separatoria Acta, 2006, (4): 67–77

7 Sulaberidze G A, Borisevich V D, Xie Q X. On some separation problems on regenerated uranium application in the fuel cycle[C]. Proceedings of IX all-Russia (International) scientific conference, “physical and chemical processes on selection of atoms and molecules”, Zvenigorod, Russia, 2004: 70–77

8 Sulaberidze G A, Borisevich V D, Xie Q X. Study of regularities of stationary mass transfer in separating cascade for enrichment of regenerated uranium[J]. Engineering Physics, 2005, (3): 15–19

9 谢全新, 李大勇, 吴建军. 回收铀分离级联计算[J]. 核技术, 2009, 32(1): 61–65

XIE Quanxin, LI Dayong, WU Jianjun. Cascade calculations for separation of recycled uranium[J]. Nuclear Techniques, 2009, 32(1): 61–65

10 贾兴国, 应纯同, 曾实. 附加供料离心净化级联的实现[J]. 清华大学学报(自然科学版), 2006, 46(3): 371–373

JIA Xingguo, YING Chuntong, ZENG Shi. Realization of centrifuge purge cascade with additional feed[J]. Journal of Tsinghua University (Science & Technology), 2006, 46(3): 371–373

11 Sulaberidze G A, Borisevich V D, Xie Q X. Quasi-Ideal cascades with an additional flow for separation of multicomponent isotope mixtures[J]. Theoretical Foundations of Chemical Engineering, 2006, 40(1): 7–16

12 Halle E V, Oak R, Tennessee. Multicomponent isotope separation in matched abundance ratio cascades with losses from each stage[C]. Proceedings 1st workshop on separation phenomena in liquids and gases, Darmstadt, Germany, 1987: 325–356

13 Sulaberidze G A, Borisevich V D. Cascades for separation of multicomponent isotope mixtures[J]. Separation Science and Technology, 2001, 36(8/9): 1769–1817

14 Borisevich V D, Sulaberidze G A, Wood H G. The theory of isotope separation in cascades: problems and solutions[J]. Ars Separatoria Acta, 2003, (2): 107–124

15 Xie Q X, Borisevich V D, Potapov D V. Multicomponent isotope mixture separation in square cascade with losses of working substances[J]. Engineering Physics, 2006, (2): 30–34

16 Song T M, Zeng S. On the optimity of separation cascade for a binary and multi-component case[C]. Proceedings of the workshop on separation phenomena in liquids and gases, Beijing, China, 2006: 132–142

17 宋天明, 曾实. 多组分气体离心分离级联的解析优化[J]. 清华大学学报(自然科学版), 2006, 46(12): 2003–2006

SONG Tianming, ZENG Shi. Optimization of centrifuge cascades for the separation of multicomponent gas mixtures[J]. Journal of Tsinghua University (Science & Technology), 2006, 46(12): 2003–2006

18 薛毅. 最优化原理与方法[M]. 北京: 北京工业大学出版社, 2001

XUE Yi. Principle and method of optimization[M]. Beijing: Press of Beijing University of Industry, 2001

19 陈卫东, 蔡明林, 于诗源. 工程优化方法[M]. 哈尔滨:哈尔滨工程大学出版社, 2006

CHEN Weidong, CAI Minglin, YU Shiyuan. Engineering optimization method[M]. Harbin: Press of Harbin University of Technology, 2006

20 Sinev N M. Economics of nuclear power engineering[M]. Moscow: Energoatomizdat, 1987

21 Zaritskaya T S, Zaritskii S M, Kruglov A K, et al. Dependence of232U formation in nuclear fuel on neutron spectrum[J]. Atomic Energy, 1980, 48(2): 67–70

22 Buttler G G, Wilcox P. Enrichment of recycled uranium[J]. Nuclear Engineering, 1986, 28(6): 186–190

23 Matveev L V, Tsentner E M. Problem of232U and236U accumulation in nuclear fuel[J]. Atomic Energy, 1980, 48(4): 10–17

CLCTL92

Optimization of quasi-ideal cascade with an additional feed flow

XIE Quanxin YANG Kun ZHOU Yongsheng MOU Hong

(Institute of Physical and Chemical Engineering of Nuclear Industry,Tianjin 300180,China)

Background:Some isotope separation tasks, for example, the enrichment of recycled uranium and the purge of light impurity, must be completed in a cascade with an additional feed flow. Purpose: It is one of the design aims for this type of cascade to determinate the configuration parameters such as the number of total stages, positions of base and additional feed flows on condition that concentrations of target components in the products and waste flows are given. Methods: In order to design the cascade theoretically, a mathematical optimization model is established for a quasi-ideal cascade. The total substance flow in the cascade is chosen as an objective function. Using penalty function method, the constraint optimization problem is transformed into an unconstraint one which was solved by a simplex method. Results: The optimization method is applied to calculate the cascade in which the recycled uranium is enriched. The results of calculation indicate that the minimum substance flow in the cascade decreases with the increasing of the abundance of235UF6in the recycled uranium. Conclusions: It is proved that the mathematical optimization model established for the quasi-ideal cascade with an additional feed flow is reasonable.

Quasi-ideal cascade, Additional flow, Optimization, Penalty function, Recycled uranium

TL92

10.11889/j.0253-3219.2013.hjs.36.060602

谢全新，男，1974年出生，2007年于莫斯科工程物理学院获博士学位，高级工程师，专业：同位素分离理论与实验研究

2013-03-11，

2013-04-25