供料位置对离心机供料射流流场影响的数值模拟
张雯成,姜东君,曾 实
(清华大学 工程物理系,北京 100084)
供料位置对离心机供料射流流场影响的数值模拟
张雯成,姜东君,曾 实
(清华大学 工程物理系,北京 100084)
为研究供料口位置对离心机供料射流流场的影响,采用直接模拟蒙特卡罗(DSMC)方法对离心机中心射流区域进行模拟。选择Iguassu离心机模型和变径硬球碰撞模型,得到了不同的轴向和径向供料位置下径向供料模型的供料射流流场参数分布情况。通过对模拟结果进行分析可得:在径向供料条件下,供料口附近区域的流场受供料条件的影响显著。由于供料射流的膨胀作用,导致了供料口附近低温区的出现。在靠近出流边界处,由于较高的角向速度,形成较大的压力梯度,使气体的径向速度降低,导致温度明显升高。轴向位置的变化导致流体参数的轴向平移。而随着供料口径向位置的增大,供料口附近的膨胀范围减小,低温区减弱,即该区域的最低温度升高。而近出流边界处,随供料口径向位置的增大,温度相应降低,径向速度同时降低。
气体离心机;稀薄流区;数值模拟
气体离心机是一中空的转子,内部充入UF6同位素混合物气体。在转子高速旋转形成的强离心场作用下,充入的气体产生分离效应。在无内部环流的情况下,其内部气体的压强在径向上呈指数分布[1]。按侧壁压强13.3kPa计算[2],对于Iguassu模型离心机[3],努森数Kn的范围为4.33×10-4~4.67×107。可见对于该模型离心机,流场在径向上跨越了自由分子流区、过渡区、滑移流动区和连续介质区等4个流区,其中自由分子流区、过渡区和滑移流动区统称为稀薄流区。
对于离心机中心区域的稀薄流区,由于连续性假设不成立,Navier-Stokes方程不再适用。因此,在离心机的流场计算中,常忽略中心的稀薄区域,仅以满足Navier-Stokes方程的连续流区为研究对象,并引入黏性边界,人工给定供料条件。但这一方法并不符合实际的流动情况,所以需对离心机内部的稀薄流区进行模拟,来得到供料射流的具体结构。
国内外学者均对该领域进行过研究。Roblin等[4]采用DSMC(Direct Simulation Monte-Carlo)方法,对径向供料模型进行了模拟,得出了流场中的速度分布情况。姜东君等[5]采用CFD方法,同样模拟了径向供料的Iguassu模型。目前,该方面的研究主要集中在径向供料的流场分布和供料速度等参数对流场的影响,对供料位置等其他参数研究得较少,因此需进行进一步的研究。
本文采用DSMC方法,对高速旋转离心机内部的供料射流区域进行模拟,针对径向供料模型,研究其不同的轴向和径向供料位置对供料射流流场的影响。
1 DSMC方法简介
DSMC方法是目前模拟稀薄流区较为合适的方法。该方法直接对流动进行模拟,由Bird[2]首先提出。其思想是将分子的运动和碰撞解耦,并用模拟分子(宏分子)代替真实的气体分子(每一个模拟分子代表大量的真实分子)。在每个时间间隔内,气体分子无碰撞地按照自身速度和当前位置自由运动。然后根据分子的位置,运用概率的方法来判断分子与分子之间或分子与壁面之间是否发生碰撞。根据分子间的碰撞模型和分子与壁面间的碰撞模型,可计算得到分子碰撞后的状态。流场中宏观量(如速度、密度、温度等)可通过对网格中的模拟分子进行统计平均得到。在DSMC方法中,分子间的碰撞模型是比较关键的问题,本文中所采用的是变径硬球模型。
2 模型及条件
2.1 离心机模型
本文采用Iguassu模型离心机[3],其主要参数列于表1。
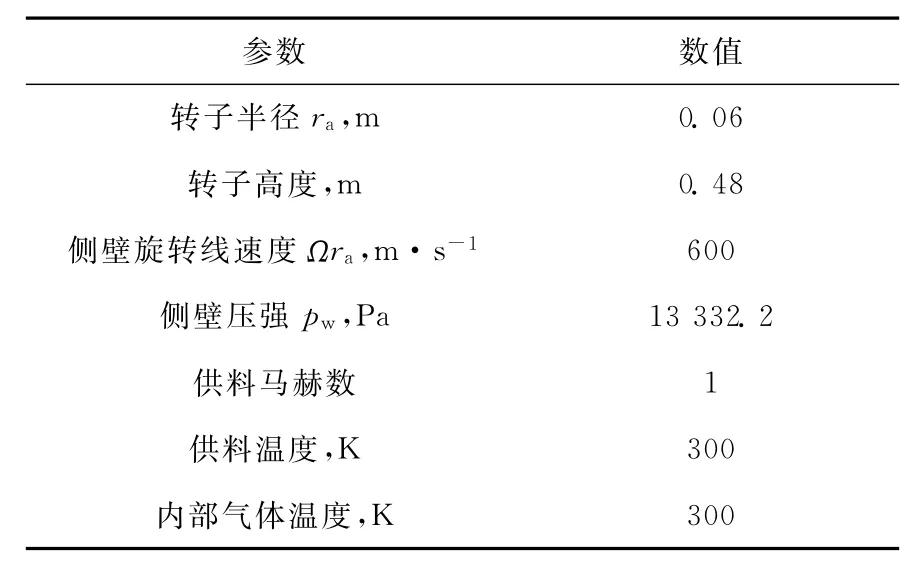
表1 Iguassu模型离心机[3]主要参数Table 1 Parameters of Iguassu model centrifuge[3]
2.2 计算模型
计算模型如图1所示,采用径向供料模型,气体由沿径向的供料口进入离心机内部,在供料口处给定供料射流的径向速度、温度和密度,不考虑供料射流的轴向和角向速度。由于离心机径向上的密度变化很大,因此越靠近侧壁,所需的模拟分子数就越多。受计算机计算能力的限制,目前尚无法开展对连续流区的DSMC模拟。因此,计算域选择为供料口附近区域,径向范围为0.005~0.05m,轴向范围为-0.12~0.12m。
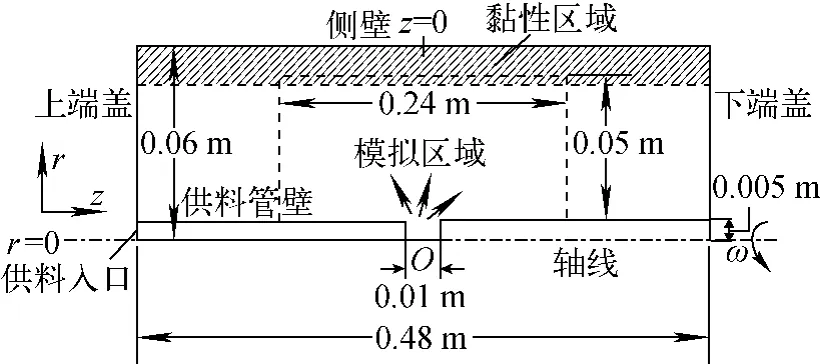
图1 计算模型Fig.1 Calculation model
2.3 气体参数
本文中所选用的气体介质为UF6,其相关参数列于表2。

表2 UF6气体相关参数Table 2 Physical properties of UF6
2.4 边界条件及初始条件
模拟中,无供料条件下的模拟区域初始状态设为均匀流,而在径向供料条件下则设为真空。
边界条件的设定如图2所示。在无供料条件下,模拟区域的下边界为固体壁面,而在径向供料条件下,模拟区域的下边界为入流边界,供料量为12mg/s,供料气体的温度为300K,马赫数为1。供料管固定,温度为300K。模拟区域的上边界为出流边界,气体的分子数密度为1.37×1021m-3,温度为300K,旋转线速度为500m/s。模拟区域的左右边界设为旋转固体壁面,温度为300K,旋转角速度为1×104rad/s。

图2 边界条件Fig.2 Boundary condition
3 计算程序
本文所用程序是在Bird[2]提供的G2程序基础上进行的再度开发,使其能适应离心机流场的特殊需求。对于轴对称流场,均匀的网格划分会导致靠近轴线的网格体积小于靠近出流边界的网格体积,再加上离心机中心区域极为稀薄的特点,靠近轴线区域的网格内分子数会远少于靠近出流边界处的。如果每个模拟分子所代表的真实分子数N为固定值,就会导致中心区域内的分子数过少,从而碰撞数过少,不利于计算的收敛和宏观量的统计平均。
为了解决这一问题,计算中设定模拟分子所代表的真实分子数N与半径r的关系为:N=krn。其中,k为常数。通过实际模拟计算,选取n=3。
4 模拟结果及分析
本文首先对无供料情况进行模拟,在此情况下,流体状态存在解析解,在半径方向上气体压强呈指数分布,速度呈线性分布v=Ωr。图3示出了无供料条件下z=0处沿径向的流动参数分布情况。可看出,密度、角向速度分布与解析解符合得较好,从而验证了本文所编DSMC计算程序的正确性。
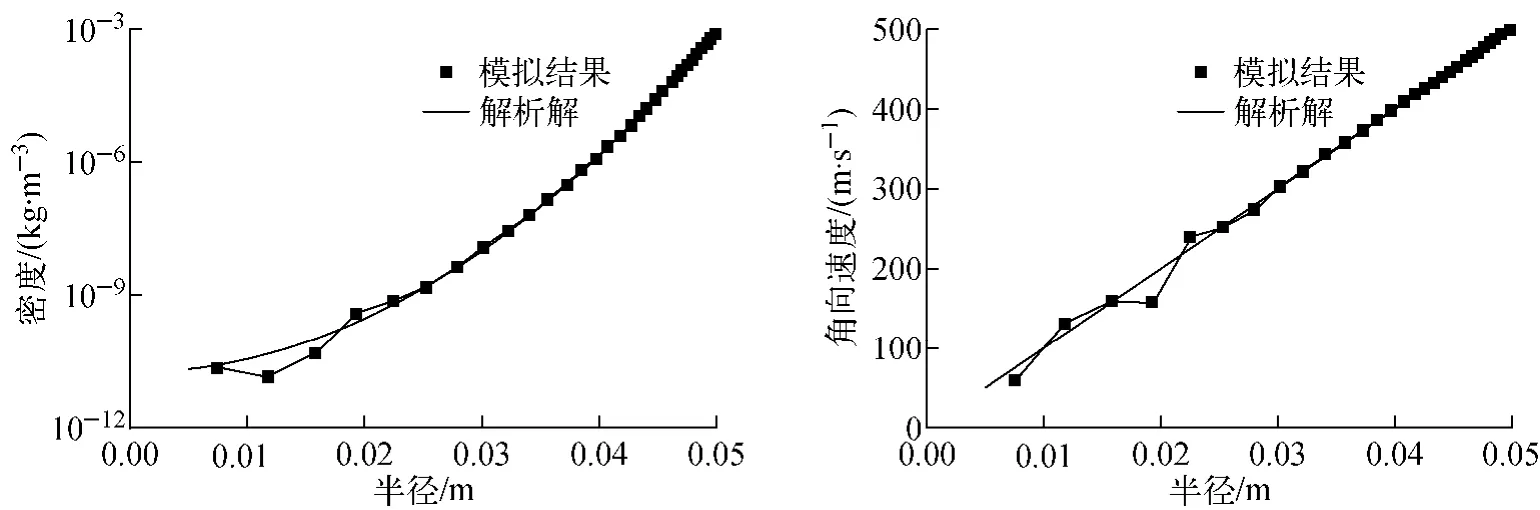
图3 无供料情况下z=0处的流体参数分布Fig.3 Distribution of gas properties on z=0on condition of no feed
固定径向供料位置r=0.005m,计算不同的轴向供料位置z为0、-0.01和-0.02m3种情况下的流场分布情况。对于实际离心机,轴向供料位置不可能位于接近端盖处。因为接近端盖处,受挡板、支臂等影响较大,在该处供料,离心机的分离功率较低[6],对实际工作无意义。因此,本文选取了较为靠近中心处的3个轴向供料位置。图4为在供料口轴向位置z为0时,流场参数的分布情况。可看出,供料口附近区域流场受径向供料的影响极为显著。由于供料射流的膨胀作用,导致了供料口附近低温区的出现。在近出流边界处,由于较高的角向速度,形成很大的压力梯度,使气体的径向速度降低,导致温度明显升高。而图5示出3种不同的轴向供料位置下,r=0.03m处的流体参数分布情况。可看出,在供料口附近的一定轴向范围内,轴向位置的变化对流场的影响不甚明显,仅使得参数的值随供料口轴向位置的平移而平移。

图4 供料口轴向位置z=0时的流场参数分布Fig.4 Distribution of gas properties on condition of feed on z=0
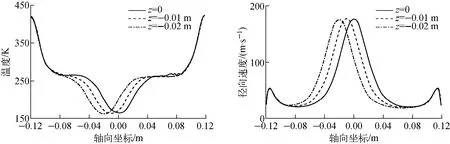
图5 r=0.03m处的流体参数分布Fig.5 Distribution of gas properties on r=0.03m
固定轴向供料位置z=0,计算不同的径向供料位置0.005、0.010和0.025m的3种情况下的流场分布情况。图6为3种情况下r=0.05m处的流体参数分布情况。可看出,随供料口径向位置的增大,由于轴向可扩散的范围减小,供料口附近的膨胀范围减小,低温区减弱。而近出流边界处,随供料口径向位置r的增大,温度相应降低,径向速度同时降低。
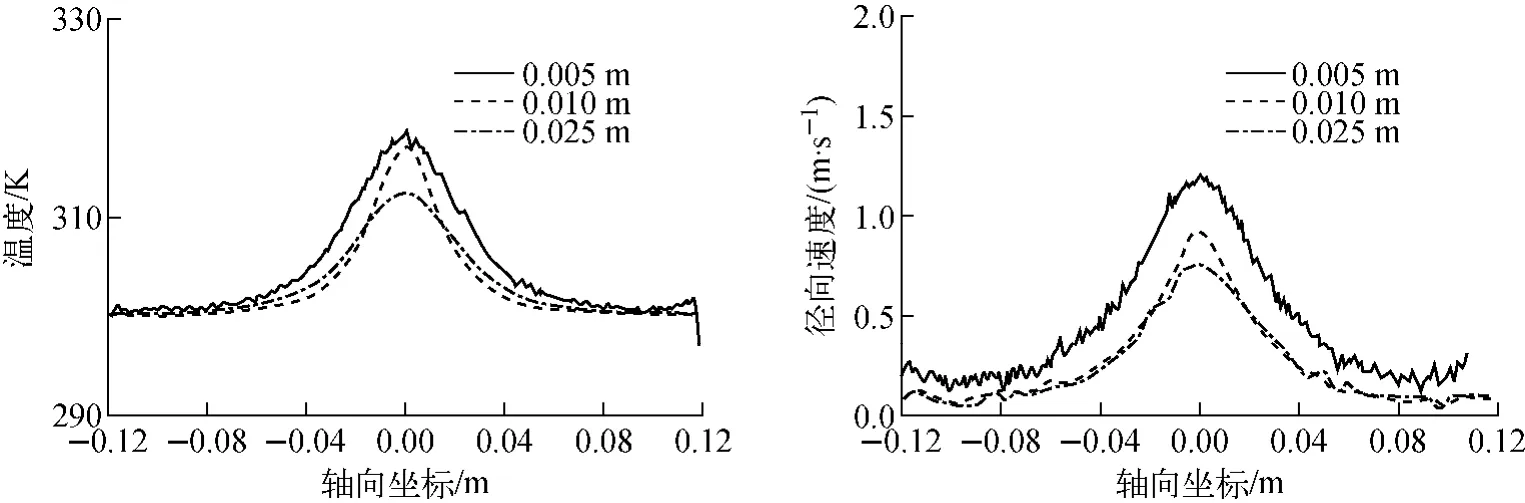
图6 r=0.05m处的流体参数分布Fig.6 Distribution of gas properties on r=0.05m
5 结论
本文采用DSMC方法,对气体离心机供料射流区域进行了模拟,给出了无供料和径向供料两种条件下该区域的流体参数分布情况。本文实现了DSMC方法对离心机供料射流区域的模拟,并通过对模拟结果进行分析,得到了以下结论:
1)在无供料条件下,离心机中心区域流场基本符合等温刚体模型。其中,气体压强沿径向呈指数分布,角向速度呈线性。
2)在径向供料条件下,供料口附近区域的流场受供料条件的影响显著。由于供料射流的膨胀作用,导致了供料口附近低温区的出现。在近出流边界处,由于较高的角向速度,形成较大的压力梯度,使气体的径向速度降低,导致温度明显升高。
3)供料口附近一定轴向范围内,轴向位置的变化对流场的影响不甚显著,仅使得参数的值随供料口轴向位置的平移而平移。
4)随供料口径向位置r的增大,供料口附近的膨胀范围缩小,低温区减弱,即该区域的最低温度升高。而近出流边界处,随供料口径向位置r的增大,温度相应降低,径向速度同时降低。因此,供料口的径向位置r对离心机的流场影响相对较为显著。
通过以上分析可看出,供料口的位置变化会给黏性边界处的参数分布带来较大影响。该影响会进一步导致离心机分离功率的变化。因此,进一步的工作应将射流区域的流场与连续流区的流场进行耦合计算,其中,连续流区的流场采用CFD的方法进行计算,结合外部连续流区的环流进行综合分析,得出供料射流的位置对离心机分离功率等指标的影响。
[1] 张存镇.离心分离理论[M].北京:原子能出版社,1987.
[2] BIRD G A.Molecular gas dynamics and the direct simulation of gas flows[M].Oxford:Clarendon Press,1994.
[3] DONEDDU F,ROBLIN P,WOOD H G.Optimization studies for gas centrifuges[J].Separation Science and Technology,2000,35:1 207-1 221.
[4] ROBLIN P,DONEDDU F.Direct Monte-Carlo simulation in a gas centrifuge[C]∥Rarefied Gas Dynamics:22ndInternational Symposium.Sydney,Australia:American Institute of Physics,2001:169-173.
[5] 姜东君,曾实.气体离心机二维供料射流的数值研究[J].原子能科学技术,2008,42(增刊):41-44.
JIANG Dongjun,ZENG Shi.2Dnumerical study of feed-jet flow in gas centrifuge[J].Atomic Energy Science and Technology,2008,42(Suppl.):41-44(in Chinese).
[6] 刘冰,姜东君,曾实.供料条件对气体离心机分离性能影响的数值研究[J].原子能科学技术,2012,46(10):1 153-1 157.
LIU Bing,JIANG Dongjun,ZENG Shi.Numerical investigation on influence of feed condition on separation performance of gas centrifuge[J].Atomic Energy Science and Technology,2012,46(10):1 153-1 157(in Chinese).
Numerical Simulation of Influence of Feed Position on Flow Field
ZHANG Wen-cheng,JIANG Dong-jun,ZENG Shi
(Department of Engineering Physics,Tsinghua University,Beijing100084,China)
In order to study the influence of feed position on the counter-current in gas centrifuge,direct simulation Monte-Carlo(DSMC)method was chosen to simulation the rarefied region of gas centrifuge.By setting Iguassu centrifuge model and variable hard sphere(VHS)model,the flow distributions of different feed positions were acquired.The analysis of the calculation results notes the following flow phenomena:In case of radial feed,the region near the feed outlet is largely influenced by the feed condition.The expansion of jet results in the hypothermic region.Near the boundary of effluent,due to the fast peripheral velocity,pressure gradient is large,which results in the slow radial velocity and the high temperature.The axial translation of the jet results in the axial translation of the flow distributions.With the increase of the radius of feed,the region of expansion near the feed reduces and the lowest temperature of the hypothermic region rises.Near the boundary of effluent,with the increase of the radius of feed,thetemperature and the radial velocity fall.
gas centrifuge;rarefied region;numerical simulation
TL25
A
1000-6931(2014)02-0331-05
10.7538/yzk.2014.48.02.0331
2012-11-11;
2013-01-05
国家自然科学基金资助项目(11075088);中俄(NSFC-RFBR)合作项目资助(11311120046)
张雯成(1989—),女,上海人,硕士研究生,核燃料循环与材料专业

