基于CFD方法的球床式高温气冷堆稳态热工水力分析

宋士雄 魏 泉 蔡翔舟 郭 威

基于CFD方法的球床式高温气冷堆稳态热工水力分析

宋士雄1,2魏 泉1,2蔡翔舟1,3郭 威1,3

1（中国科学院上海应用物理研究所 嘉定园区 上海 201800）
2（中国科学院大学 北京 100049）
3（中国科学院核辐射与核能技术重点实验室 上海 201800）

基于CFD通用计算程序Fluent，开发了多孔介质流固两相局域非热平衡模型，对PBMR-400满功率名义工况下稳态热工水力行为进行了分析。高温气冷堆堆芯的热工水力计算模型通常为带有强内热源宏观的多孔介质模型，Fluent程序本身的多孔介质模型为局域热平衡模型，无法恰当描述堆芯热工水力行为。通过开启Fluent的自定义标量场(UDS)功能并在动量方程上附加阻力源项，实现了局域非热平衡模型，能够精确地计算球床堆堆芯热工水力行为。CFD程序使用了非常精细的网格，可以计算更加精细的流场和温场分布。计算表明，Fluent的结果与国际上著名的球床堆热工水力程序THERMIX，TINTE符合较好，可以作为球床堆热工水力分析工具。

CFD (Computational Fluid Dynamics)，高温气冷堆，多孔介质

准确可靠的反应堆热工水力分析对于球床式高温反应堆的设计是非常重要的。目前国际上球床式高温气冷堆热工水力行为分析程序THERMIX[1−3]和TINTE[4–5]，均采用二维轴对称局域非热平衡多孔介质模型，流场方程为附加多孔介质阻力源项的准静态方程，冷却剂温场和固相球床的温场分别独立求解，各个模块之间进行迭代并收敛。随着计算机性能的大幅度提高以及算法的改进，在反应堆设计及研究中CFD (Computational Fluid Dynamics)方法开始被采用[6–7]，并且实现了CFD程序与中子学程序、系统热工程序的耦合计算[8−10]。Becker等[11]基于CFD开发了球床反应堆热工程序，通过与SANA装置的实验结果比较，验证了程序的适用性。

CFD程序在计算过程中可以使用更加精确的流体力学方程与很精细的网格，因此可以对局部流场、温场进行更加精确的分析。本文基于通用CFD程序Fluent[12–13]开发了局域非热平衡多孔介质模型。流场求解采用Fluent的SIMPLE算法解算器，气体冷却剂的温场方程求解使用Fluent自带的能量场方程解算器，固相温场方程通过附加标量场方程UDS (User Defined Scalar)来求解，流固两相的热耦合通过交换源项来实现。使用Fluent的UDF (User Defined Function)功能，实现了球床边界与反射层边界的热耦合，冷却剂边界与反射层边界的热耦合。

PBMR-400 (Pebble Bed Module Reactor)是南非国营电力设计的热功率为400 MW、电功率为165MWe的模块式高温气冷球床式反应堆[14–15]。反应堆堆芯直接连接氦气轮机，设置了具有闭路直接循环特征的能量转换单元，堆芯燃料球采用环形布置，具有很强的非能动余热排出能力。反应堆堆芯活性区共有大约452000个燃料球，内外半径分别为1.0 m、1.85 m，活性区高度为11 m。堆芯运行压力为9 MPa，入口冷却剂温度约为500 °C，出口氦气温度约为900 °C，堆芯的平均功率密度为4.8MW·m−3。本文基于Fluent的自定义标量场及自定义函数功能开发了局域非热平衡多孔介质模型，对PBMR-400满功率名义工况的热工水力行为进行了分析，验证了程序的适用性。

1 计算模型和方法

1.1理论模型

本文采用了简化的二维轴对称模型，以堆芯中心反射层圆心为对称轴线，模型包括：(1)堆芯多孔介质区；(2)中心反射层区；(3)外部反射层。边界条件：Fluent对边界条件有几类方式，通过测试不同的边界条件对计算结果的影响，并考虑程序的收敛性。本文中采取速度入口，压力出口边界，在计算过程中通过调节出口表压，使入口压力达到反应堆的操作压力，程序自身的操作压力设置为0 MPa。在压力9 MPa，温度773 K工况下，入口质量流193kg·s−1折算入口速度为4.5875 m·s−1。出口条件为压力出口，表压为8.73 MPa。外部反射层热边界条件为固定温度边界773 K，反射层与球床热边界设置为非耦合边界，使用UDF自定义边界条件。简化后的模型经网格无关性验证后使用48400个计算网格如图1所示。

图1 计算网格Fig.1 Calculation mesh.

二维轴对称模型的控制方程如下，其中物理量均为体积平均的表观物理量，

连续性方程：

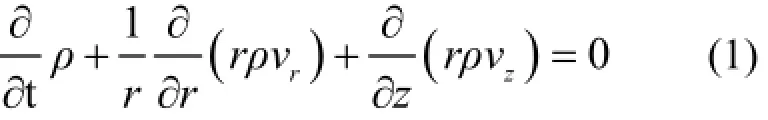
轴向动量方程：

径向动量方程：

动量源项：

式中，Ψ是球床的阻力因子，ε为球床的孔隙率，μ为氦气的动力学粘度。本文使用德国Nuclear Safety Standards Commission KTA[16]推荐的阻力因子：

式中，雷诺数Re=ρvDp/μ。

冷却剂能量场方程：

固相球床的能量场方程：

式中，Q.为单位体积内的功率密度，W·m−3。为流固两相之间的热传导项。

主要采用KTA[17–18]推荐的物性和热工参数：

密度：ρ=48.14P/T(1+0.4446P/T1.2)−1

定压比热容：Cp=519 J/kg·K

定容比热容：Cv=3177 J/kg·K

动力学粘度：μ=3.674×10−7×T0.7Pa·s

氦气冷却剂的热传导系数：kf=2.682×10−3×(1+ 1.123×P)×T0.711−0.0002×PW·m−1·K−1

球床的热传导系数的计算采用Zehner-Schlunder[19]模型。

1.2计算方法简介

Fluent带有一个基于局域热平衡假设的多孔介质计算模型，流固两相的热传导方程合并为一个总的能量场方程，热传导系数通过流固两相体积权重平均得到。对于不含内热源的，或流固两相之间温度梯度不大的多孔介质模型，局域热平衡模型的理论计算能给出和实验符合较好的结果。高温气冷堆堆芯具有强内热源，流固两相的温度梯度较大，局域热平衡假设的多孔介质模型在这种工况下就不再适用。本文不使用Fluent自带的多孔介质模型，在基于表观速度的动量方程上附加新的阻力源项式(4)表征多孔介质区域的流动行为。氦气冷却剂的能量场方程(6)使用Fluent的流体能量场方程，开启标准的湍流模式。固相球床的温场方程(7)的求解通过开启Fluent中的UDS来实现，流固两相在迭代过程中交换源项，实现温场的耦合计算。堆芯多孔介质区域与中心反射层和外部反射层的热传导包括堆芯流体和反射层的热传导、堆芯固相球床和反射层的热传导，热边界的耦合通过在边界上设置自定义函数根据壁面温差调节热通量来实现。

程序计算流程图见图2。

图2 计算流程图Fig.2 Computation program flow diagram.

2 PBMR-400满功率名义工况热工水力分析

名义工况下，PBMR-400堆芯冷却剂入口质量流率为193 kg·s−1，入口温度为500 °C(773 K)，出口温度约为900 °C(1173 K)，运行压力9 MPa。基准参考堆芯的功率密度(MW·m−3)分布如表1所示，堆芯径向1.85 m共5个分区，轴向11 m共22个分区[20](R/Z为堆芯径向/轴向坐标位置)。

表1 PBMR-400基准参考功率分布Table 1 PBMR-400 Benchmark power density.

图3是堆芯冷却剂温场及反射层温场分布，堆芯冷却剂温场最热的区域位于堆芯最下方靠近中心反射层的出口位置，最高温度达到1210 K。出口处的平均温度约为1172 K。中心反射层距顶部3 m左右，靠近堆芯球床一侧的温度高于相同高度上的堆芯流场温度，从该处开始堆芯功率密度的提高使得球床固相温度升高很快，堆芯固相球床向中心反射层的热传导相对于流相热传导比例加大，这一区域的冷却剂被中心反射层和球床加热(图3、图4数据相对于中心轴线做了对称处理)。

堆芯固相温场(UDS0标量场)分布距顶部从3 m左右开始升高到1100 K以上(图4)，堆芯固相最热的区域位于堆芯中下部靠近中心反射层的区域，固相温场的最高温度达到1220 K。

图3 堆芯冷却剂及反射层温场分布Fig.3 Coolant and reflector temperature distribution.

图5 (a)显示，堆芯不同轴向位置上冷却剂温度的径向分布较为均匀。球床固相在中心反射层附近区域出现了较大的温降(图5b)，温度降低的原因在于此处的空隙率较大，流场的流速相对较高(图6)，热对流传导效率较高。外反射层附近区域温度下降较快的原因是此区域孔隙率较高，流速较快，虽然此处的功率密度略有上升，但是由于流体与固相球床对流传热性能的提高，固相的温场仍下降较显著。

图4 球床固相温度分布Fig.4 Solid phase temperature.

堆芯内总压降为2.76×105Pa(图7)，略小于TINTE及THERMIX的计算结果，部分原因在于本文中采取的简化堆芯模型，堆芯底部的出流区域引起的压降没有考虑在内。

图5 不同轴线位置处冷却剂温度分布(a)和固相温度分布(b)Fig.5 Fluid temperature (a) and solid phase temperature (b) distribution.■ z=10.95m, ● z=7.85m, ▲ z=5.45m, ▼ z=2.45m, ◄ z=0.75m

图6 冷却剂速度分布Fig.6 Fluid velocity distribution.

图7 堆芯压降分布Fig.7 Reactor core pressure drop.

3 程序的比较和验证

表2中的结果表明，本文的计算结果与球床式高温气冷堆热工流体程序THERMIX与TINTE的结果符合较好。堆芯氦气冷却剂的平均温度，固相球床的平均温度，以及氦气出口温度的相对偏差如表2所示，与国际通用的高温气冷球床堆热工程序主要计算结果的偏差均在可以接受的范围之内。

表2 Fluent结果和THERMIX、TINTE[21−23]的比较Table 2 Calculation result comparison between CFD and THERMIX, TITE.

4 结语

本文基于CFD通用计算程序Fluent，研究了高温气冷堆PBMR-400稳态热工水力行为。通过Fluent的自定义函数功能，开发了局域非热平衡的多孔介质模型，计算了反应堆内冷却剂的温场分布和固相球床的温场分布，分析了堆芯流场及不同轴线位置处的温场分布。通过和国际上应用广泛的球床式高温气冷堆热工水力程序计算结果比较，表明基于CFD的高温气冷堆热工计算结果与THERMIX与TINTE符合的较好，CFD程序可用于球床式反应堆堆芯热工水力行为的分析。本文分析了PBMR-400稳态热工水力行为，在此工作的基础上可以继续开发瞬态热工水力计算程序并和中子学程序耦合，研究反应堆堆芯反应性引入以及失压失冷等事故工况下堆芯的瞬态热工水力行为。

1 Petersen K. Zur Sicherheitskonzeption des Hochtemperaturreaktors mit natiirlicher Warmeableitung aus dem Kern im Storfall[R]. FZ Jülich, Germany, 1972

2 Struth S. Thermix-Direkt: Ein Rechenprogramm zur instationären zweidimensionalen simulation thermohydraulischer transienten[R]. FZ Jülich, Germany, 1985

3 Cleveland J C, Greene S R. Application of THERMIX-KONVEK code to accident analyses of modular pebble bed high temperature reactors (HTRs)[R]. NUREG/CR-469 ORNL/TM-9905, 1986

4 Gerwin H, Scherer W. The two-dimensional reactor dynamics programme TINTE. Part1: basic principles & methods of solution[R]. Jül-2167: TINTE Part: 1, 1987

5 Gerwin H, Scherer W, Teuchert E. The TINTE modular code system for computational simulation of transient processes in the primary circuit of a pebble-bed high-temperature gas-cooled reactor[J]. Nuclear Science Engineering, 1989,103: 302−312

6 Smith B L. Assessment of CFD codes used in nuclear reactor safety simulations[J]. Nuclear Engineering and Technology, 2010,42(4): 339−364

7 李林森, 王侃, 宋小明. CFD在核能系统分析中应用的最新进展[J]. 核动力工程, 2009,5(增刊): 28−33

LI Linsen, WANG Kan, SONG Xiaoming. International research progress of CFD application in analysis of nuclear power system[J]. Nuclear Power Engineering, 2009,5(Supp): 28−33

8 桂学文, 蔡琦, 陈玉清. 基于CFD的反应堆局部三维流动模型与时空中子动力学模型耦合研究[J]. 核科学与工程, 2010,3: 216−222

GUI Xuewen, CAI Qi, CHEN Yuqing. Study on coupling of local three-dimension flow model based on CFD method and space-time neutron kinetics model[J]. Nuclear Science and Engineering, 2010,3: 216−222

9 刘余, 张虹, 贾宝山. 核反应堆热工水力多尺度耦合模拟初步研究[J]. 核动力工程, 2010, (s1): 11−15

LIU Yu, ZHANG Hong, JIA Baoshan. Preliminary research on nuclear reactor thermal-hydraulic multi-scale coupled simulation[J]. Nuclear Power Engineering, 2010, (s1): 11−15

10 刘余, 张虹, 贾宝山. RELAP5与CFX程序耦合研究[J].原子能科学技术, 2010, 44(3): 304−308

LIU Yu, ZHANG Hong, JIA Baoshan. Research on coupling between RELAP5 and CFX codes[J]. Atomic Energy Science and Technology, 2010,44(3): 304−308

11 Becker S, Laurien E. Three-dimensional numerical simulation of flow and heat transport in high-temperature nuclear reactors[J]. Nuclear Engineering and Design, 2003,222: 189−201

12 Fluent 6.3 User’s Guide. Fluent Inc.http://aerojet.engr. ucdavis.edu/fluenthelp/html/ug/main_pre.htm, 2006

13 Fluent 6.3 UDF Manual. Fluent Inc.http://aerojet.engr. ucdavis.edu/fluenthelp/html/udf/node2.htm, 2006

14 Mulder E, Teuchert E. Plutonium disposition in the PBMR-400 high temperature gas-cooled reactor. PHYSOR, Chicago, 2004

15 Mulder E. Core basic design report for the PBMR nuclear power plant project[R]. PBMR Report, Doc. No.02979-34

16 KTA 3102.3. Reactor core design of high-temperature gas-cooled reactors Part 3: loss of pressure through friction in pebble bed cores[S].1981

17 KTA 3102.1. Reactor core design for high-temperature gas-cooled reactor part 1: calculation of the material properties of helium[S]. 1978

18 KTA 3102.2. Reactor core design of high-temperature gas-cooled reactors part 2: heat transfer in spherical fuel elements[S]. 1983

19 Zehner P, Schlunder E U. Thermal conductivity of granular materials at moderate temperatures[J]. Chemie Ingenieur Technik, 1970,42: 933−941

20 Gougar H D. The application of the PEBBED code suite to the PBMR-400 coupled code benchmark. Idaho National Laboratory Idaho Falls, Idaho 83415, 2006

21 Boer B, Lathouwers D, Kloosterman J L, et al. Validation of the DALTON-THERMIX code system with transient analyses of the HTR-10 and application to the PBMR. 2010,170(2): 306−321

22 Dudley T, Bouwer W, Piet de Villiers, et al. The thermal-hydraulic model for the pebble bed modular reactor (PBMR) plant operator training simulator system[J]. Nuclear Engineering and Design, 2008,238: 3102−3113

23 Boer B, Kloosterman J L, Lathouwers D, et al. In-core fuel management optimization of pebble-bed reactors[J]. Annals of Nuclear Energy, 2009,36: 1049−1058

CLCTL349

High temperature gas-cooled pebble bed reactor steady state thermal-hydraulics analyses based on CFD method

SONG Shixiong1,2WEI Quan1,2CAI Xiangzhou1,3GUO Wei1,3
1(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China)
2(University of Chinese Academy of Sciences, Beijing 100049, China)
3(Key Laborotary of Nuclear Radiation and Nuclear Energy Technology, Chinese Academy of Sciences, Shanghai 201800, China)

Background:Based on general purpose CFD code Fluent, the PBMR-400 full load nominal condition thermal-hydraulics performance was studied by applying local thermal non-equilibrium porous media model.Purpose:In thermal hydraulics study of the gas cooled pebble bed reactor, the core of the reactor can be treated as macroscopic porous media with strong inner heat source, and the original Fluent code can not handle it properly.Methods:By introducing a UDS in the calculation domain of the reactor core and subjoining a new resistance term, we develop a non-equilibrium porous media model which can give an accurate description of the core of the pebble bed. The mesh of CFD code is finer than that of the traditional pebble bed reactor thermal hydraulics analysis code such as THERMIX and TINTE, thus more information about coolant velocity fields, temperature field and solid phase temperature field can be acquired.Results:The nominal condition calculation results of the CFD code are compared to those of the well-established thermal-hydraulic code THERMIX and TINTE, and show a good consistency.Conclusion:The extended local thermal non-equilibrium model can be used to analyse thermal-hydraulics of high temperature pebble bed type reactor.

CFD (Computational Fluid Dynamics), Gas-cooled pebble bed reactor, Porous media

TL349

10.11889/j.0253-3219.2013.hjs.36.120601

中国科学院战略性先导科技专项资助项目(XDA02010200)资助

宋士雄，男，1983年出生，2011年于兰州大学获硕士学位，现为中国科学院上海应用物理研究所博士研究生，反应堆热工水力

2013-09-05，

2013-11-05