2A12铝合金本构关系和失效模型

张伟，魏刚，肖新科

(哈尔滨工业大学 高速撞击研究中心，黑龙江 哈尔滨150080)

0 引言

2A12 铝合金为可热处理的强化铝合金，具有良好的塑性成形能力和机械加工性能，是航空航天领域中使用最广泛的铝合金之一［1］。随着计算机和数值计算方法的发展，数值模拟成为研究工程中结构的大变形甚至材料和结构破坏问题的重要手段，但是材料的动态本构关系一直是束缚其发展的瓶颈［2］。国产2A12 铝合金的常温准静态力学性能和高应变率行为，高温下力学性能可以从公开文献中获得一些报道。高玉华［3-4］对LY12CZ(即2A12)的准静态和动态拉压性能进行了实验研究，结果表明2A12 是应变率不敏感材料。谢若泽等［5］使用霍普金森压杆对高温高率下LY12 的动态压缩性能进行了研究，结果表明高于200 ℃时，温度软化效应明显;在103～104范围内应变率效应不明显。李春雷［2］使用准静态和霍普金森压杆研究了不同温度、不同应变率下国产2A12 铝合金的力学行为，并拟合出了Johnson-Cook 强度模型所需要的模型参数。对于2A12 铝合金的失效机制研究有一些零星的报道。李棠等［6］对2A12 铝合金光滑圆棒和缺口拉伸试样的断裂机制进行了研究，结果表明2A12 铝合金的断裂形式对应力状态非常敏感。司马爱平［7］研究了LY12 随应力三轴度变化时两种断裂形式，即正拉断和剪断。

本文使用万能材料试验机对2A12 在常温至250 ℃的准静态力学行为进行研究，并同时使用霍普金森拉杆实验和Taylor 撞击实验考查其应变率敏感性，结合扭转和压缩实验获得了2A12 的失效应变与应力状态(应力三轴度)的关系。基于实验结果，参考文献［8］的思想修改了Johnson-Cook 强度模型中的应变强化项和Johnson-Cook 失效模型中的温度软化项，并结合数值仿真获得了相应的模型参数。修改后的Johnson-Cook 模型的预测结果与实验吻合很好，证明了模型的有效性。

1 2A12 的力学性能实验

实验所用原材料为16 mm 直径的2A12 棒料，东北轻合金有限责任公司产。该棒料热处理状态为T4.材料的具体化学成分(质量百分数)为:Si(0.6%)，Fe(0.7%)，Cu(0.05%)，Mn(1.0%)，Zn(0.10%)，其余为Al.

1.1 准静态实验及结果

光滑圆棒试样名义直径为6 mm，标距段长30 mm.使用Shimadzu AG-Ⅰ万能材料试验机进行了室温和100 ℃、150 ℃、200 ℃、250 ℃的准静态拉伸实验。使用DVE-101 视频引伸计跟踪了标距段的伸长量，引伸计跟踪的标距段的长度为25 mm，名义应变率为1.11 ×10-3s-1.

图1给出了不同温度下单向拉伸实验中得到的载荷位移曲线，图2给出了屈服强度与失效应变随温度的变化。由于没有明显的屈服平台，屈服强度统一取0.2%塑性应变时对应的工程应力。失效应变定义为εf=ln(A0/Af)，其中A0、Af分别为试样的初始面积和拉断后断口的面积。

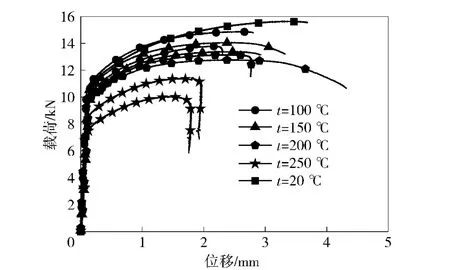
图1 不同温度下2A12 单向拉伸载荷位移曲线Fig.1 Load-displacement curves of 2A12 at various temperatures

图2 屈服强度和失效应变随温度的变化Fig.2 Variations of yield strength and fracture strain versus temperature

由图2可以看出，屈服强度随温度的升高而降低，但降低幅度不是太明显;失效应变随温度的升高明显提高，在250 ℃时，失效应变达到了常温时的3 倍以上。实验中常温下断口表现为倾斜的杯锥口状，说明2A12 材料表现出了一定的脆性，韧性不是特别好;高温下表现为比较明显的杯锥口状。

失效应变通常依赖于应力状态，如应力三轴度，即平均应力与等效应力的比值(应力三轴度σ*=σH/σeq，其中σH为平均应力，σeq为等效应力)。为了考察失效应变与应力三轴度的关系，开展了常温下圆柱压缩、扭转和缺口拉伸实验。使用Instron 5500 试验机对名义直径12.4 mm，长径比分别为0.8、1、1.5、2 的圆柱试样进行了常温压缩试验，得到的压缩屈服强度为384.6 MPa，这与得到的拉伸屈服强度400.0 MPa 仅差4%左右，试样沿与轴线呈45°方向开裂。使用电子扭转试验机开展了6 mm直径光滑圆棒试样的扭转实验，获得了扭矩-转角曲线，扭断后发现断口平齐，未见颈缩。对缺口曲率半径为3 mm 和9 mm，缺口处名义直径6 mm 的圆棒试样进行了常温拉伸试验，得到了载荷-位移曲线，拉断后断口表现为杯锥口状。光滑圆棒拉伸，圆柱压缩，扭转及缺口拉伸试样典型断裂形式如图3所示;图4和图5给出了扭转及缺口拉伸试样的载荷-位移曲线，图中20 和30 分别代表数值模拟中试样半径方向划分网格的个数。

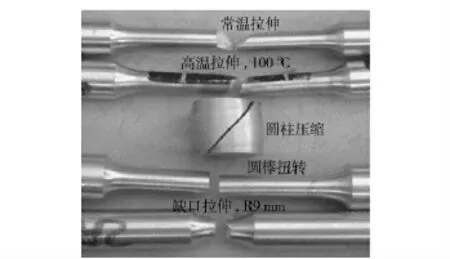
图3 几种准静态实验得到的试件典型断口形式Fig.3 Fracture patterns in several kinds of quasi static tests

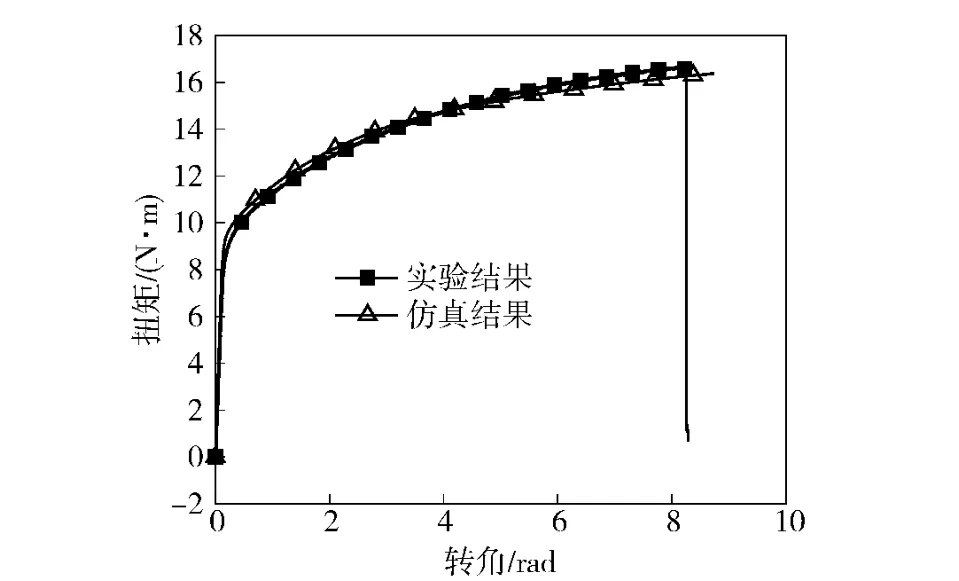
图4 扭矩转角曲线Fig.4 Torque-angel in the torsion test

1.2 动态拉伸实验及结果

为了考察应变率的影响，在霍普金森拉杆设备上开展了动态拉伸实验，应变率从800～1 400 s-1，获得的典型应力-应变曲线如图6(包括准静态下的单向拉伸应力-应变曲线)。需要说明的是，在动态拉伸过程中，试件并未拉断。从图6可以看出，2A12 存在一定的应变率强化效应，但不是太明显。值得注意的是，可能由于实验手段或设备的原因，应变率范围不够宽，动态拉伸应力-应变曲线抖动较大，不易准确得到动态下屈服强度。

1.3 Taylor 撞击实验及结果

Taylor 撞击实验经常被用来获取或者校准材料参数［8-10］。在轻气炮上进行了名义直径12.62 mm，长度50.82 mm 的2A12 圆柱形弹体正撞击高强装甲钢板的实验，得到了撞击后弹体长度与头部直径数据及变形破坏形式，见表1.实验中，装甲钢板未见明显变形。

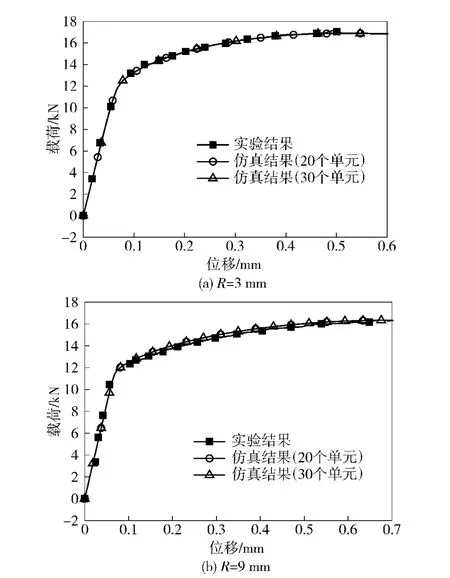
图5 缺口试样拉伸载荷-位移曲线Fig.5 Load-displacement curves of notched specimens

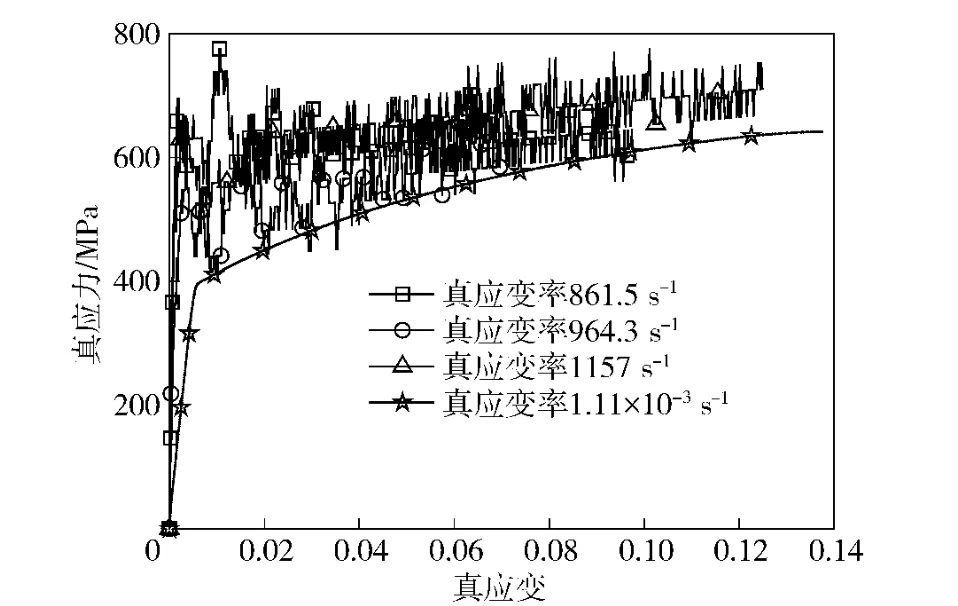
图6 2A12 动态拉伸曲线与准静态对比Fig.6 Comparison of dynamic and quasi static tension curves of 2A12

表1中，mp为弹体质量，L0和D0分别为弹体初始长度和直径，Le和De分别为实验中得到的撞击后弹体长度和头部直径，Ls和Ds分别为数值模拟中得到的撞击后弹体长度和头部直径。

2 2A12 的本构模型和失效准则

2.1 本构关系

Johnson-Cook［11］本构模型因其形式简单，物理意义明确，参数较容易获取，且能很好地描述金属材料的应变、应变率及温度效应，经常被作为金属材料的本构关系用在数值模拟中。尝试在Johnson-Cook模型的基础上描述2A12 材料的力学行为。Johnson-Cook 模型表达式为

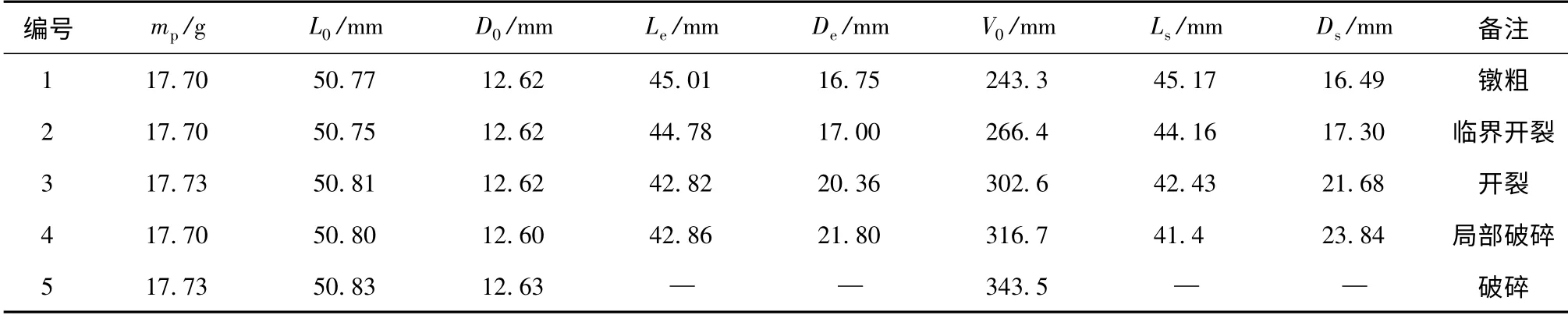
表1 Taylor 撞击实验结果Tab.1 Taylor impact test results

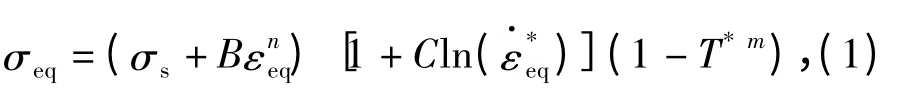
式中:σs为材料在参考应变率和参考温度下的屈服强度;B 和n 为应变强化系数;C 为应变率敏感系数;m 为温度软化系数;σeq为等效应力;εeq为等效塑性应变为无量纲化等效塑性应变率，为参考应变率;T*=(T -Tr)/(Tm-Tr)为无量纲化温度，Tr为参考温度293 K，Tm为材料的熔点863 K，T 为当前温度。

2.1.1 准静态力学行为

用Johnson-Cook 模型对常温下光滑圆棒试样的等效应力-应变曲线(颈缩前)进行拟合(ε·0取准静态拉伸下应变率，Tr取室温293 K)，得到σs=400.0 MPa，B=989.0 MPa，n =0.654，此组参数记为JC1.由于实验中试样断裂处出现了略微的颈缩，拟合过程中只使用颈缩前的数据。如果考虑颈缩失稳条件(即颈缩处满足dσeq/dεeq= σeq)，拟合得到σs=400.0 MPa，B=424.0 MPa，n =0.350，记为JC2.为考察Johnson-Cook 模型的预测结果，使用这两套参数分别对准静态常温下的拉伸实验进行仿真，在ABAQUS/STANDARD 中建立二维轴对称计算模型，固定试样的一端，对另一端施加位移。图1(a)给出了模拟得到的载荷-位移曲线与实验的对比。JC1模拟得到的载荷-位移曲线与实验比较接近，但不能预测颈缩现象;JC2 虽然能预测到颈缩，但得到载荷-位移曲线与实验形式差距较大。

借鉴文献［8］的方法，使用分段形式的表达式代替Johnson-Cook 模型中σs+Bεneq一项，在颈缩前采用Voce 形式，即

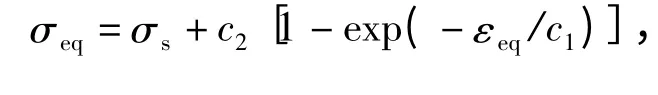
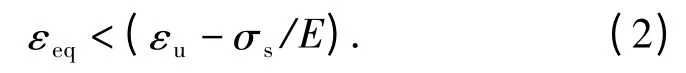
式中:c1和c2为材料参数;E 为弹性模量;εu为颈缩时的真应变。颈缩后的流动应力表示为

式中:σu为颈缩时的真实应力;w 为介于0～1 之间的权值。可以通过调整w 的大小经数值仿真得到颈缩后的应力-应变曲线。该方法来自于文献［12］，被证明简单有效。

实验结果表明，E=71.7 GPa，σu=635.0 MPa，εu=0.125 5;通过对颈缩前的应力-应变关系拟合得到c1=0.071 3，c2=288.0 MPa;通过使用二维轴对称模型的数值仿真，确定了w=0.图7(b)给出了此时的预测结果，可以看出，预测结果与实验吻合非常好。半径方向划分20 个单元和30 个单元对预测结果影响很小，证明了预测的有效性。

2.1.2 温度对屈服强度的影响

对不同温度下单向拉伸实验得到的屈服强度，使用Johnson-Cook 强度模型中的温度软化项进行拟合，得到温度软化系数m=1.426.

2.1.3 应变率对屈服强度的影响

直接从动态拉伸应力-应变曲线获取屈服强度比较困难，所以很难直接得到应变率敏感系数C.在Johnson-Cook 本构模型中，除C 以外的其他参数都已经获得，所以可以参考文献［8］的方法，通过Taylor 实验反算得到C.

使用ABAQUS/EXPLICIT 对Taylor 实验进行3D 数值模拟，与实验比较弹体剩余长度和头部直径，可以确定应变率敏感系数C.

由材料手册可知，2A12 的密度ρ =2.77 g/cm3，比热cp=921 J/(kg·K).撞击过程中的温升表达为其中χ 为塑性功转热系数，取常值χ=0.9.

图7 原始JC 与修改的JC 对单向拉伸载荷位移曲线的预测Fig.7 Comparison of load-displacement curves between the test result and model predictions

装甲钢靶板由于在撞击中变形很小，借用文献［13］双线性硬化模型来描述其本构关系，并忽略应变率对其强度的影响，不考虑其在撞击过程中的温升。模型及参数如下:σeq=σs+Etεeq.其中屈服强度σs=1.9 GPa，弹性模量E =204 GPa，切线模量Et=15 GPa，密度ρ=7.85 g/cm3，泊松比μ=0.33.

使用前面得到的模型和参数进行数值模拟，仅改变C 值，通过和实验结果比较，得到C =0.001.实验及仿真结果见表1.

2.2 失效模型

Johnson-Cook 失效模型包含了应力三轴度、应变率以及温度对失效应变的影响，适合于描述金属在高温高应变率下的破坏现象。基于Johnson-Cook失效模型描述2A12 的失效行为，原始的Johnson-Cook 失效模型表达式［14］如下:

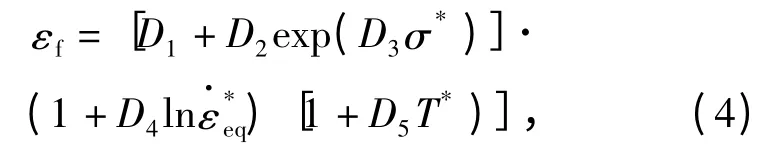
式中D1～D5均为材料参数。

根据准静态圆柱压缩实验、圆棒扭转实验、单向拉伸实验以及带缺口的拉伸实验可以得到失效应变与应力三轴度的关系。通过Bridgman［15］的分析，可近似取拉伸试样中的应力三轴度表示为ln［1 +a/(2R)］.式中:a 为拉伸试样有效半径;R为缺口处曲率半径。扭转和压缩的应力三轴度分别为0 和-1/3.由于断口直径或面积不易直接测量准确，对拉伸和扭转实验，采用获得的本构关系对原始实验进行数值模拟，对比获得的载荷-位移曲线，找到实验中试样断裂时对应的仿真中的等效应变，即认为是该试样的失效应变，此方法已有许多成功应用，如文献［8，16 -17］等。对扭转实验的模拟采用二维轴对称模型，固定试样的一端，对另一端施加扭角。数值模拟得到的载荷-位移曲线与实验有较好的一致性，如图4，图5和图7。对得到的断裂应变拟合得D1=0.116，D2=0.211，D3= -2.172.图8给出了数值仿真得到的断裂应变(压缩为实验值)，其中的曲线是拟合断裂应变值得到的。

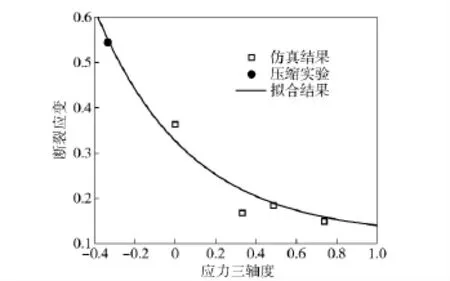
图8 断裂应变与应力三轴度的关系Fig.8 Fracture strain versus stress triaxiality

Johnson-Cook 失效模型中的温度软化项为温度的一次函数，从图2可以看出，不同温度下拉伸实验得到的断裂应变与温度并不呈线性关系。参考文献［8］，将温度软化项修改为指数形式，修改后的失效模型表示为

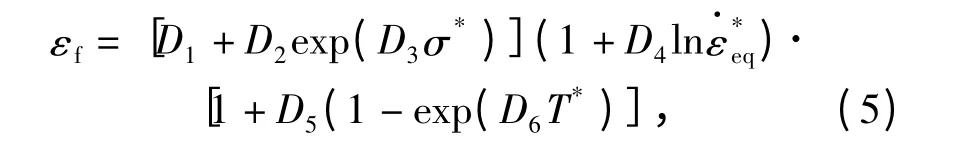
式中D1～D6为材料参数。

D1～D4与原始Johnson-Cook 失效模型一致，拟合不同温度下的单向拉伸实验失效应变，得到D5=-0.012 56，D6=13.04.

除应变率相关系数D4外，本构和失效模型的其他参数都已得到，可以通过反算Taylor 实验中临界开裂的工况得到D4.由表1可知，v0=266.4 m/s时，弹体临界开裂。使用ABAQUS/EXPLICIT 3D 仿真时发现，D4=0.012 时，计算结果与实验吻合较好，如图9.

图9 Taylor 撞击实验临界开裂实验与仿真比较(v0 =266.4 m/s)Fig.9 Comparison of the deformation and fracture obtained in experiment and predicted by numerical simulation

2.3 模型参数的实验验证

综上，2A12 本构和失效模型及参数全部得到，综合如表2所示。

利用得到的参数对较高速度下Taylor 撞击实验(表1中实验3～5)进行数值模拟，模拟设置与2.1.3 相同，弹体半径方向划分30 个网格(参考文献［8］).仿真获得的变形与破坏形式与实验吻合很好，如图10.由此可见，本文使用的2A12 本构和失效模型及获取的参数是可靠的。

3 结论

图10 较高速度下Taylor 撞击实验与仿真结果对比Fig.10 Comparison of the deformation and fracture modes in Taylor tests with high speed

表2 2A12 所有模型参数Fig.2 All model parameters of 2A12

通过准静态拉伸、压缩、扭转实验，霍普金森拉杆动态拉伸实验和Taylor 撞击实验，并结合数值模拟，研究了2A12 铝合金的准静态、动态以及高温本构关系和失效模型。实验结果表明:2A12 的应变强化效应明显，应变率敏感性较弱，温度软化效应明显;失效应变随应力三轴度增加而减小，随温度升高而增加，随应变率增加而增加。

基于实验结果，对Johnson-Cook 强度模型的应变强化项和Johnson-Cook 失效模型的温度软化项进行了修改，并拟合得到了相关参数。修改后的模型给出了与实验吻合较好的预测结果。

通过对较高速度下Taylor 撞击实验的模拟，与实验比较撞击后弹体变形与破坏形式，验证了模型及参数的有效性和可靠性。

References)

［1］ 吴大方，宋昊，高镇同，等.铝合金2A12 在热冲击条件下的力学性能［J］.北京航空航天大学学报，2007，33(5):531 -534.WU Da-fang，SONG Hao，GAO Zhen-tong，et al.Mechanical properties of 2A12 Al alloy at transient heating［J］.Journal ofBeijing University of Aeronautics and Astronautics，2007，33(5):531 -534.(in Chinese)

［2］ 李春雷.2A12 铝合金本构关系实验研究［D］.哈尔滨:哈尔滨工业大学，2006.LI Chun-lei.Experimental investigation into the constitutive relationship of 2A12 aluminum alloy［D］.Harbin:Harbin Institute of Technology，2006.(in Chinese)

［3］ 高玉华.铝合金LC4 和LY12CZ 在高应变率拉伸和压缩下的本构关系［J］.材料科学与工艺，1994，2(2):25 -29.GAO Yu-hua.Dynamic compression and tensile properties of Al alloys LC4 and LY12CZ at high strain rate［J］.Material Science and Technology，1994，2(2):25 -29.(in Chinese)

［4］ 高玉华.铝合金LC4 和LY12CZ 应变率相关力学性能的实验研究［J］.上海力学，1995，16(1):62 -66.GAO Yu-hua.An experimental study of rate-dependence materials Al-alloys LC4 and LY12CZ［J］.Shanghai Journal of Mechanics，1995，16(1):62 -66.(in Chinese)

［5］ 谢若泽，张方举，邓志方，等.高温高应变率LY12 铝压缩动态力学性能实验［J］.航空动力学报，2009，24(4):799 -803.XIE Ruo-ze，ZHANG Fang-ju，DENG Zhi-fang，et al.Experimental investigation into dynamic compressive mechanical properties of LY12 at high strain rates and high temperatures［J］.Journal of Aerospace Power.2009，24(4):799 -803.(in Chinese)

［6］ 李棠，王清远，岳珠峰.铝合金2A12 韧性断裂机制的实验研究［J］.实验力学，2006，21(6):763 -768.LI Tang，WANG Qing-yuan，YUE Zhu-feng.Experimental studies on ductile fracture mechanism of aluminum alloy 2A12［J］.Journal of Experimental Mechanics，2006，21(6):763 -768.(in Chinese)

［7］ 司马爱平.应力三维度对材料断裂破坏的影响［D］.上海:上海交通大学，2009.SIMA Ai-ping.Influence of stree triaxiality on material fracture［D］.Shanghai:Shanghai Jiaotong University，2009.(in Chinese)

［8］ 张伟，肖新科，魏刚.7A04 铝合金的本构关系和失效模型［J］.爆炸与冲击，2011，31(1):81 -87.ZHANG Wei，XIAO Xin-ke，WEI Gang.Constitutive relation and fracture model of 7A04 aluminum alloy［J］.Explosion and Shock Waves，2011，31(1):81 -87.(in Chinese)

［9］ Allen D J，Rule W K，Jones S E.Optimizing material strength constants numerically extracted from taylor impact data［J］.Experimental Mechanics，1997，37(3):333 -338.

［10］ 陈刚，陈忠富，陶俊林，等.45 钢动态塑性本构参量与验证［J］.爆炸与冲击，2005，25(5):451 -456.CHEN Gang，CHEN Zhong-fu，TAO Jun-lin，et al.Investigation and validation on plastic constitutive parameters of 45 steel［J］.Explosion and Shock Waves，2005，25(5):451 - 456.(in Chinese)

［11］ Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strains，high strain rates and high temperatures［C］∥Proceedings of the seventh international symposium on ballistics.Hague:IBC，1983:541 -547.

［12］ Ling Y.Uniaxial true stress-strain after necking［J］.AMP Journal of Technology，1996，(5):37 -48.

［13］ Børvik T，Hopperstad O S，Berstad T，et al.A computational model of viscoplasticity and ductile damage for impact and penetration［J］.European Journal of Mechanics-A/Solids，2001，20(5):685 -712.

［14］ Johnson G R，Cook W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Engineering Fracture Mechanics，1985，21(1):31 -48.

［15］ Bridgman P W.Studies in large plastic flow and fracture［M］.Harvard:Harvard University Press，1964.

［16］ Bao Y，Wierzbicki T.A comparative study on various ductile crack formation criteria［J］.Journal of Engineering Materials and Technology，2004，126(3):314 -324.

［17］ Wierzbicki T，Bao Y，Lee Y，et al.Calibration and evaluation of seven fracture models［J］.International Journal of Mechanical Sciences，2005，47(4 -5):719 -743.