惰性气体消除膛内残余燃气可燃性的应用研究

徐滨，刘志涛，季丹丹，王浩宇，廖昕，王泽山

(南京理工大学 化工学院，南京210094)

0 引言

火炮在射击过程中可能存在炮尾焰等不良射击现象，对使用带来一定影响［1-2］。消焰剂的加入或消焰剂含量的增加可以解决炮尾焰的问题，但是消焰剂作为一种不含能量或者含能极低的物质填入药室，会使膛压上升较快，弹丸初速增加不明显，对弹道性能是不利的［3］。由于发射药燃气中CO 通常占燃气总量的一半左右［4］，消焰剂的加入并未减少可燃气体中含有的有毒成分，对于密闭坦克来说，残余燃气会随着开闩而扩散至坦克舱内，危害射手和操作人员的健康。为降低发射药燃气的可燃性和毒性，可采用提高发射药装药氧平衡、身管安装抽烟装置或采用高压气体将残余燃气吹出炮管的方法［5］。在火炮膛内装有用于吹出膛内有害气体的气瓶同样能够达到降低膛内燃气危险隐患的目的。实验研究表明:N2、CO2等惰性气体能有效抑制可燃气体的燃烧与爆炸［6-7］。在开闩前使用惰性气体将膛内残余可燃气体吹出炮膛是将燃气可燃性和毒性降低至最小程度的积极有效方法。

本文通过对发射药燃烧过程建模分析得到燃气组成，结合内弹道计算弹丸出炮口时的膛底压力数据，对气瓶放气完全后膛内残余燃气和气瓶释放出的惰性气体的混合气体可燃性进行分析，得到完全消除燃气潜在危险的惰性气体质量范围。结合气瓶设计参数，论证了所得气体质量在实际使用中的可行性，以解决工程实际问题。

1 所需惰性气体质量

1.1 燃气可燃性分析

1.1.1 燃气组成

发射药在燃烧过程中满足质量守恒、化学平衡、能量守恒和高温高压下气体状态方程，忽略生成的固体产物量，采用三项截短维里方程来描述高温高压燃气状态，可建立发射药燃气模型如下:

假设燃气在喷出过程中与外界没有热交换，燃气组成一定，则开闩时的燃气组成与最大压力时燃气组成保持不变，可由模型(1)式得到。

1.1.2 燃气可燃性

可燃气体浓度在低于爆炸下限时，可燃气体既不燃烧也不爆炸;在高于爆炸上限时不会爆炸，但会着火［8］。

混合可燃气体的着火点以可燃成分中最低的着火点为准，其爆炸极限由［9-11］计算得到。

式中:

(3)式原式与实际情况不符，故添加修正系数A.爆炸下限计算时取A = -1;计算爆炸上限时，结合H2、CO、CO2和N2混合气实例［7-8，12］，实际发射药燃气计算中取

(2)式～(3)式中:LT为原整体燃气的爆炸极限(%);Xa为原燃气的折算空气含量(%);LN为不含氧、含惰性气体(无空气基燃气)的爆炸极限(%);XN为无空气基气体中惰性气体的体积分分数;Lm为混合可燃气体的爆炸极限(%);L1，L2，L3，…，Ln为组成混合可燃气体各单独可燃组分的爆炸极限;V1，V2，V3，…，Vn为各单独可燃组分在混合可燃气体中的浓度(体积百分数)。

1.2 燃气状态

1.2.1 膛压

弹丸离开膛口瞬间膛压可由内弹道方程组获得。在弹丸飞离膛口断面后，燃气从炮口喷出，由于燃气速度大于弹丸速度，继续作用于弹丸底部推动弹丸加速前进，直到火药燃气对弹丸的推力和空气的阻力相平衡时为止，此时弹丸速度增至最大值，随后燃气向四周扩散压力大幅下降，直至与大气压平衡。一般开闩时膛内压力与大气压持平。

1.2.2 温度

开闩瞬间的温度求解可分为两个部分:首先，求出弹丸飞出炮口瞬间燃气的温度T1;然后，以T1为起始条件，求出开闩瞬间燃气温度。

弹丸运动期间，燃气的温度在变化，其瞬间温度T 可用下式［2］求出:

式中:m1为虚拟质量，即将次要功对能量的消耗等同于增加弹丸质量，m1=φm，其中φ 为次要功计算系数，m 为弹质量;γ 为比热容比;mp为装药量;Ψ 为发射药已燃质量百分比;n 为燃气的量;v 为弹丸速度;η 为用以表征热散失的系数，是热散失与弹丸、气体动能的比值。

如果燃气组分的化学反应是冻结的，热损失系数η 可用下式［2，13］求出:

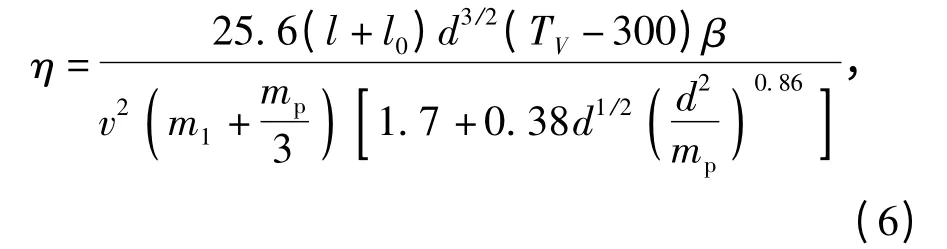
式中:β 为炮膛粗糙程度的系数，一般可取1.25;l 为弹丸行程，即身管长;l0为药室长其中V0为药室容积，S 为炮膛横截面积。

假设燃气流动过程中与外界没有热交换，燃气组成一定，不考虑气体与管壁之间的摩擦和燃气内部的摩擦，这就是一个绝热过程。若将燃气当理想气体处理，记弹丸出炮口时膛内燃气为状态1，膛内压力降至1 atm 时膛内燃气为状态2，由绝热方程［14-15］，有:

1.3 开闩时残留燃气质量

将膛内燃气近似作理想气体，在膛压分别为最大压力和常压时，存在:

式中:记最大膛压为状态3;膛内降至常压为状态2;m 为气体质量;p 为压力。

通常情况下，发射药燃烧后产生的固体产物是极微量的。当忽略这些固体产物质量时，产生最大压力的燃气总质量即为装药量。

1.4 降低燃气可燃性所需惰性气体的质量

在惰性气体释放过程中，若忽略惰性气体与燃气混合均匀的部分，可得到所需最大惰性气体质量。由于气瓶放气过程非常短暂，为简化计算，可做出如下假设:在添加惰性气体时，1)燃气各组分已达到平衡;2)燃气中各成分之间的平衡不发生变化;3)燃气温度的变化对可燃性的影响较小，可直接忽略，残余燃气做等压膨胀;4)添加过程中无空气混入。若不考虑气瓶放气对残余燃气的吹出作用，将燃气的体积百分数降至燃气爆炸下限以下所需的惰性气体质量即为降低残余燃气可燃性所需的最大惰性气体质量，即式中:Vg、Vi分别为燃气体积、添加的惰性气体体积;ng、ni分别为燃气物质的量、惰性气体物质的量。

由(8)式，得

式中:Mri为惰性气体分子量;pmax为最大膛压;p1atm为1 个大气压;mg、mi分别为燃气和惰性气体质量。

1.5 残余燃气性质及消除其可燃性所需CO2 的质量

以气瓶内所装惰性气体为CO2为例，CO2在弹丸离开炮口后开始释放，在开闩之前完全释放，所需CO2的质量由1.1 节～1.4 节模型和公式计算得到。由于发射药在弹丸出炮口之前已经燃尽，故Ψ=1，燃气参数γ 及TV由1.1.1 节中模型求得的燃气组成结果进一步计算可得，其值列于表1，v、p1由内弹道方程组可求得，对于一定的m、V0、l 和S，结合(5)式～(7)式求得的弹丸出炮口时和膛内压力降至大气压时的燃气温度计算结果见表1.

表1 计算用参数和燃气温度计算结果Tab.1 Parameters used in calculation and the corresponding results of gas temperature

表1显示，当膛内压力降至大气压时，燃气温度约306 ℃.由于整个温度计算过程中不考虑燃气与外界的热交换，因此所求燃气温度是实际膛压降至大气压时燃气温度所能达到的最大极限值。因为开闩时膛内压力约为1 个大气压，可认为表1所列结果是开闩瞬间的最高燃气温度。

对于已知配方的发射药，其燃气组成由1.1 节模型计算可得，相应的，不考虑其他因素的影响，计算时忽略空气中其他气体成分，仅考虑N2和O2，氮氧体积比近似取nN2∶nO2为3.8∶1，由(2)式～(4)式可得到其燃气可燃性。计算时将燃气燃烧环境以标准状态考虑，水作为惰性气体处理，H2的爆炸极限为4%～75.6%，CO 的爆炸极限为12.5%～74.2%.

图1为按(2)式～(4)式理论计算的燃气爆炸极限随添加CO2的体积分数变化趋势。可见，若使得燃气和CO2的混合气体不具有爆炸性，需使得混合燃气中CO2体积分数位于曲线右侧白色区域。若使得燃气和CO2的混合气体不具有可燃性，需使得混合燃气中CO2体积分数位于灰色区域下边界以下区域。

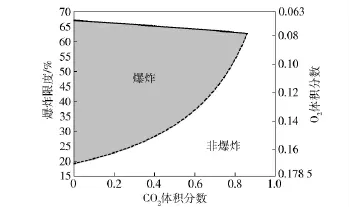
图1 燃气爆炸极限随添加CO2 体积的变化趋势Fig.1 Explosion limit trend of propellant gas with increasing volume of CO2 added

结合1.1.1 节模型求得的燃气组成和维里方程求得p1.假设燃气压力降低过程中燃气组成不变，当装药量一定时，对于一定膛内体积V，得到不同温度下压力降至大气压时膛内残余燃气质量。由CO2分子量MrCO2为44.01 及(9)式求得所需添加CO2的质量mi，见图2.

图2 使燃气不燃烧需要添加的CO2 质量随温度变化图Fig.2 Quantity of CO2 required to eliminate the flammability of residual gas at various temperatures

图2可看出若要使燃气不发生二次燃烧，当膛压降至大气压时，燃气温度为306 ℃，此时该发射药燃气不燃烧所需CO2的最小质量约为51 g.

考虑到压力、温度对燃气可燃性的影响，并且燃气的爆炸下限会随着温度的升高而降低，使得燃气可燃范围变大［16-17］，因此实际应用中应以常温下燃气不燃烧需添加的CO2的量作为实际中CO2用量的参考标准。由图2可知所需CO2的最大质量约为115 g.

2 可行性分析

对于装有计算所得质量的惰性气体气瓶，给定气瓶是否能够正常工作，在开闩前能否放气完毕，需要进一步进行可行性研究。

2.1 压力

2.1.1 气瓶开瓶压力和放气压力

用于吹出膛内残余燃气的惰性气体存放于气瓶中，其放气性能受到很多因素的影响，如气瓶内初始压力、环境条件、气体介质的状态等［18］。在实际工程实际问题中，常将其简化为绝热放气过程或等温放气过程［19-20］。

工程界广泛采用R-K 方程，以及以R-K 方程为基础的各种修正式描述真实流体状态。其中较成功的是1972年Soave 提出的修正式，称为RKS 方程，其形式为

式中a、b 为气体临界温度Tc、临界压力pc等物理性质参数的函数。

气瓶开瓶压力、放气压力可由(10)式得到。

2.1.2 膛底最大压力

由装药产生的膛底最大压力可由内弹道方程组计算得到。

2.2 放气时间

记气瓶容积为Vb，瓶内气体量ω，设瞬间的每秒流量为G，假定气体流出过程完全绝热，则流量方程［14］可表示为

式中:K0仅是绝热指数k 的函数;p0和T0指气体静止状态的参量;Sc为临界断面面积，即指通过这一断面的流量和通过其他任一断面的流量相等;φ2为消耗系数，在光滑管道的情况下，φ2一般取0.95 左右。

记气体的起始温度、压力分别为T1、p1.在气体流出的某一瞬间t，膛内温度、压力分别为T、p，记相对量由于f=RT1，且在气体运动过程中p0和T0用平均p 和T 处理，记式［14］可写作:

式中A 为流量系数，它的大小决定于绝热指数和火药力的常量，A 值可查表［14］。

(11)式，(12)式在临界条件下才能应用。这里的临界状态指气流流速由亚音速区转变为超音速区的状态。只要容器内的压力大于临界压力，就可以保证气体在临界状态下流出［14］。

当气体从容器中不断流出时，外界压力为1 atm，与之相应的临界压力pc［14］为

与此相应的总时间ts则表示为

2.3 装有所得质量范围的CO2 气瓶实际应用可行性分析

由1.5 节计算结果可知，在装药及装药量一定的情况下，为降低该装药膛内残余燃气的可燃性，所添加CO2的理论质量范围为51～115 g.已知CO2临界压力为7.376 MPa，临界温度为304.2 K［21］，在这个CO2质量范围内，对于给定的气瓶参数，利用RKS 方程计算得到常温下气瓶开瓶压力p1、放气压力p0的范围，结果列于表2.

表2 常温下气瓶压力及放气时间计算结果Tab.2 The calculation results of the required pressure and the deflation time of gas bottle at room temperature

不考虑发射药燃烧过程中对气瓶的热传递，将气瓶做常温处理，由(11)式，CO2的绝热指数k =1.3，对应K0=2.090，临界压力计算得pc=0.19 MPa.pc计算结果小于p0，故气瓶放气时间可用2.2 节中公式计算，结果列于表2.

初速、最大压力和弹丸出炮口时炮口压力、对应膛底压力可由内弹道计算得到。燃气的绝热指数k可近似取为比热比γ，其值见表1，火药力f 可由燃气组成结果进一步计算得到，其对应流量系数A 列于表3.当弹丸飞出炮口后，膛内燃气喷出，燃气的临界压力和膛压降至临界压力所用时间可用(13)式、(14)式计算得到，结果列于表3.

气瓶利用膛内压力开启。表2中可见所用气瓶的开瓶压力不高于26.4 MPa，而弹丸发射过程中产生的最大压力远高于气瓶的开瓶压力，能够满足气瓶开启压力的需要。但气瓶并不会在开启后立即放气，而是在膛内压力降低至低于气瓶的放气压力后才开始放气。表2中可见所用气瓶的放气压力不高于9.2 MPa.从表3的结果中可看出从弹丸飞出炮口后膛内压力降低至10 MPa 所用时间约为6 ms，即气瓶在弹丸飞出炮口6 ms 后开始放气。

表3 计算用参数及计算压力、时间结果Tab.3 The parameters used in calculation and its corresponding results of pressure and time

表3可看出，膛内压力从弹丸出炮口到降至临界压力所需时间约为60 ms.待膛内气压降至1 个大气压，火炮开闩，因此开闩时间距离弹丸飞出炮口的时间至少经过60 ms，而此时气瓶放气时间不少于54 ms.尽管54 ms 少于表2中气瓶的放气时间，但是实际上由膛内压力降至临界压力的时刻至开闩仍需要一段时间，这段时间足够气瓶将气体完全放出，因此可认为气瓶在开闩时已经完全放气。

从表2和表3的压力和时间结果可看出，装有计算所得的CO2质量的气瓶在膛内能够正常开启，并且能够放气完全。使用装有计算所得质量CO2的气瓶来降低膛内残余燃气是可行的。

3 气瓶放气及应用效果的实验验证

3.1 气瓶放气时间

采用高速摄影拍摄常温下气瓶放气过程，得到常压下气瓶放气时间。使用中止实验模拟实际火炮膛内情况，在实验中建立相同的最大压力，在相同实验条件下对使用气瓶和与气瓶体积相等的假瓶实验得到的p-t 曲线进行比较，得到气瓶的开瓶压力和放气时间之间的关系如图3所示。

图3 中止实验气瓶与假瓶压力曲线对比Fig.3 The extinction test curves of gas bottle and its compared fake bottle

图3为中止实验中气瓶与假瓶压力曲线对比。当膛内压力低于气瓶放气压力后由于气瓶放气使得气瓶曲线高于假瓶曲线。从表2、表3中对比可看出膛内压力从气瓶放气压力下降至临界压力所用时间少于气瓶放气时间，显然残余燃气的喷出速度高于气瓶放气速度。随着气瓶放气压力与膛内残余燃气之间压力差的增加，气瓶放气速度由慢变快，反映在图3中即为两条曲线明显分开，此时压力约在2.8 MPa，显然气瓶开始放气时间应略高于2.8 MPa.随着气瓶放气完毕，两条曲线分开一段时间后又重合，期间曲线分开的时间可认为是气瓶的放气时间。气瓶放气时间的理论计算结果和实验结果列于表4.

表4 气瓶放气压力与时间的理论计算值和实验结果Tab.4 The theoretical and experimental results of the pressure and the time for gas bottle to deflation

表4中可见中止实验气瓶放气时间长于表2中气瓶在常温常压下理论放气时间，这是因为在实际使用中，气瓶放气的大部分时间内膛内压力高于常压，因此实际中气瓶放气的流速小于理想值，使得放气时间大于常温常压下理论放气时间。并且理论计算值只计算气瓶压力降至临界压力所用时间，会导致理论计算值比实验值略小。同时由于实验中不可预测的因素影响，实际放气时间会大于理论计算放气时间。

现场高速摄影实验表明，从弹丸飞离炮口后到开闩之间的时间在300 ms 以上，长于表4中气瓶模拟实验放气时间，因此可认为，在开闩时气瓶内的CO2已经全部释放完毕。

3.2 残余燃气CO 浓度测试

射击后炮尾CO 浓度峰值反映CO2消除膛内残余燃气的效果。使用CO 红外光谱测试仪测得开闩后炮尾CO浓度峰值，结果列于表5.由表5可见，CO2的添加量明显对残余燃气中CO 浓度大小有影响，理论计算所得到的最大CO2添加量能够取得最好的消除残余燃气安全隐患的效果。

表5 开闩时CO 浓度测试结果Tab.5 Test results of CO concentration at breech opening

4 结论

为消除燃气可燃的隐患，采用CO2作为惰性气体混合弹丸飞出后膛内残余燃气来使得燃气不再具有可燃性。得到以下结论:

1)通过对发射药燃烧过程建立模型，对指定配方的发射药进行了燃气可燃性分析，在此基础上得到使该配方发射药残余燃气不再具有可燃性所需添加的CO2质量范围:51～115 g.考虑到实际温度、压力对燃气可燃范围的影响，实际中应以115 g 作为消除燃气可燃性的CO2用量。

2)对所得CO2的质量范围结合气瓶实际情况进行可行性分析。理论计算表明，装有计算所得CO2质量的气瓶在膛内能够正常开启并放气完全。

3)通过高速摄影、中止实验等方法，验证装有计算所得CO2质量的气瓶的放气压力、放气时间符合实际需要。

4)炮尾燃气CO 浓度结果表明，当添加的CO2质量越接近理论计算所需CO2质量的最大值时，CO2消除残余燃气的效果越明显。故应将计算所得最大CO2质量作为实际应用中CO2的用量。

References)

［1］ 吴毅，董朝阳，李幼林.105 mm 炮射导弹发射装药的一种优化设计方案［J］.弹道学报，2006，18(2):60 -63.WU Yi，DONG Chao-yang，LI You-lin.Optimum design for propellant charge of 105 mm gun-launched missile［J］.Journal of Ballistics，2006，18(2):60 -63.(in Chinese)

［2］ 王泽山，何卫东，徐复铭.火药装药设计原理与技术［M］.北京:北京理工大学出版社，2006.WANG Ze-shan，HE Wei-dong，XU Fu-ming.Design principles and technology of charge［M］.Beijing:Beijing Institute of Technology Press，2006.(in Chinese)

［3］ 王育维，魏建国，郭映华，等.消焰剂对模块装药内弹道性能影响分析［J］.火炮发射与控制学报，2009，(4):12 -15.WANG Yu-wei，WEI Jian-guo，GUO Ying-hua，et al.Influence of flame suppressor on interior ballistics characteristics of modular charge［J］.Journal of Gun Launch and Control，2009，(4):12 -15.(in Chinese)

［4］ 王琼林，蒋树君，余斌，等.炮射导弹发射药燃气中CO 浓度的影响因素［J］.火炸药学报，2006，29(6):61 -64.WANG Qiong-lin，JIANG Shu-jun，YU Bin，et al.The factors affecting monoxide(CO)concentration in propellant combustion gas of a gun-propelled laser-guided missile propelling charge［J］.Chinese Journal of Explosives ＆ Propellants，2006，29(6):61 -64.(in Chinese)

［5］ 贺增弟，吕智星，袁治雷，等.硝酸铵对炮射导弹发射药燃气中CO 浓度的影响［J］.火炸药学报，2010，33(2):82 -85.HE Zeng-di，LU Zhi-xing，YUAN Zhi-lei，et al.Effects of ammonium nitrate on CO concentration in combustion gas of a gun shooting guided missile propelling charge［J］.Chinese Journal of Explosives ＆ Propellants，2010，33(2):82 -85.(in Chinese)

［6］ 李成兵，吴国栋，周宁，等.N2/CO2/H2O 抑制甲烷燃烧数值分析［J］.中国科学技术大学学报，2010，40(3):288 -293.LI Cheng-bing，WU Guo-dong，ZHOU Ning，et al.Numerical analysis of methane combustion suppression by N2/CO2/H2O［J］.Journal of University of Science and Technology of China，2010，40(3):288 -293.(in Chinese)

［7］ 王华，葛岭梅，邓军.惰性气体抑制矿井瓦斯爆炸的实验研究［J］.矿业安全与环保，2008，35(1):4 -7.WANG Hua，GE Ling-mei，DENG Jun.Experimental study of using inert gas to suppress mine gas explosion［J］.Mining Safety ＆Environmental Protection，2008，35(1):4 -7.(in Chinese)

［8］ 潘功配，杨硕.烟火学［M］.北京:北京理工大学出版社，1997.PAN Gong-pei，YANG Shuo.Pyrotechnics technology［M］.Beijing:Beijing Institute of Technology Press，1997.(in Chinese)

［9］ 汪佩兰，李桂茗.火工与烟火安全技术［M］.北京:北京理工大学出版社，1996.WANG Pei-lan，LI Gui-ming.Safety technology for pyrotechnics and fireworks［M］.Beijing:Beijing Institute of Technology Press，1996.(in Chinese)

［10］ Liekhus K J，Zlochower I A，Cashdollar K L，et al.Flammability of gas mixtures containing volatile organic compounds and hydrogen［J］.Journal of Loss Prevention in the Process Industries，2004，13:377 -384.

［11］ Liao S Y，Cheng Q，Jiang D M，et al.Experimental study of flammability limits of natural gas-air mixture［J］.Journal of Hazardous Materials，2005，B119:81 -84.

［12］ 魏永生，周邦智，郑敏燕.H2、CO、CH4混合气体爆炸极限的多元回归分析［J］.化学研究与应用，2004，16(3):419 -420.WEI Yong-sheng，ZHOU Bang-zhi，ZHENG Min-yan.The multivaried regression analysis of polybasic explosive mixture gas containing H2，CO and CH4［J］.Chemical Research and Application，2004，16(3):419 -420.(in Chinese)

［13］ Conner J.Theory of interior ballistics of guns［M］.New York:John Wiley，1950.

［14］ 华东工学院103 教研室.内弹道学［M］.北京:国防工业出版社，1978.103 Research Room in East China Institute of Technology.Interior ballistics［M］.Beijing:National Defense Industry Press，1978.(in Chinese)

［15］ 傅献彩，沈文霞，姚天扬.物理化学［M］.第4 版.北京:高等教育出版社，2003.FU Xian-cai，SHEN Wen-xia，YAO Tian-yang.Physical chemistry［M］.4th ed.Beijing:Higher Education Press，2003.(in Chinese)

［16］ 王淑梅，梅林.可燃性气体爆炸极限与温度、压力的关系［J］.安全技术，1998，(2):24 -25.WANG Shu-mei，MEI Lin.Relationships between explosion limit of flammable gas and temperature pressure［J］.Safety Technology，1998，(2):24 -25.(in Chinese)

［17］ 田贯三，于畅，李兴泉.燃气爆炸极限计算方法的研究［J］.煤气与热力，2006，26(3):29 -33.TIAN Guan-san，YU Chang，LI Xing-quan.Study on calculation method of gas explosion limits［J］.Gas ＆ Heat.2006，26(3):29 -33.(in Chinese)

［18］ 李超，梁浩，王飞，等.容器放气性能研究［J］.机械科学与技术，2011，30(1):163 -165.LI Chao，LIANG Hao，WANG Fei，et al.A study of the outgassing characteristics of a vessel［J］.Mechanical Science and Technology for Aerospace Engineering，2011，30(1):163 -165.(in Chinese)

［19］ 金英子，朱祖超，杨庆俊，等.气动系统充放气过程中气体状态多变指数的简化与确定［J］.机械工程学报，2005，41(6):76 -79.JIN Ying-zi，ZHU Zu-chao，YANG Qing-jun，et al.Simplification and determination of polytropic exponent of thermodynamic process in the filling and exhausting process in a pneumatic system［J］.Chinese Journal of Mechanical Engineering，2005，41(6):76 -79.(in Chinese)

［20］ 李军，李玉军，王祖温.气动充放气系统的流场计算［J］.机床与液压，1999，(4):24 -26.LI Jun，LI Yu-jun，WANG Zu-wen.The calculation of flow field in charging and discharging system for pneumatic system［J］.Machine Tool ＆ Hydraulics，1999，(4):24 -26.(in Chinese)

［21］ David R Lide.Handbook of chemistry and physics［M］.Maryland，USA:CRC Press，2004.