平面镜成像问题再讨论

陈 雁

（浙江省宁波市镇海教师进修学校，浙江 宁波 315200）

1 用平面镜成像的基本原理对竞赛题进行简明求解

本刊2012年第11期刊登了“对一道竞赛题的再思考”，以下简称“再思考”，文章对竞赛题的错误答案进行了分析，并给出了正确的结果.但文章中关于为何成7个像的讨论和作图过于复杂，本文试着用平面镜成像的基本原理，简明得出成像的个数.

图1

“再思考”一文讨论的竞赛题：如图1所示，房间内一墙角处相临两墙面挂了两个平面镜，两平面镜相互垂直，在该墙角紧靠镜面处放有一个脸盆，盆内有水.某学生通过镜面和水面最多能看到自己像的个数为

（A）3个. （B）6个. （C）9个 （D）无穷.

原题答案是选项（B），是错误的.正确的结论应该能看到7个像.

竞赛题中，脸盆内的水可以看作水平面上的平面镜.因此，本题就相当于研究3面互相垂直平面镜的成像问题.

平面镜成像特点：像与物关于镜面对称.

先讨论2面互相垂直的平面镜成像，如图2所示.M1、M2为互相垂直的平面镜.S1、S2是一次反射成像：S1是物体经过平面镜M11次反射成的像，S2是物体经过平面镜M2成的像；S12是物体先经过M1再经过M22次反射后所成的像.由于M1、M2互相垂直，所以物体先经过M1后经过M2反射所成的像S12与先经M2后经M1反射所成的像S21刚好重叠，物体S共成3个像.

图2

3面互相垂直的平面镜的成像如图3所示.M1、M2、M3为互相垂直的平面镜.根据平面成像特点，物体在平面镜M1、M2所成的3个像连同物体S，在平面镜M3中成4个像，所以物体S在3面互相垂直的平面镜中共成7个像.7个像中，3个是正立的，4个是倒立的；其中S123是物体经过3次反射后所成的像.由于3个平面镜互相垂直，使得3次反射所成的像S123、S132、S213、S231、S312、S321重叠.

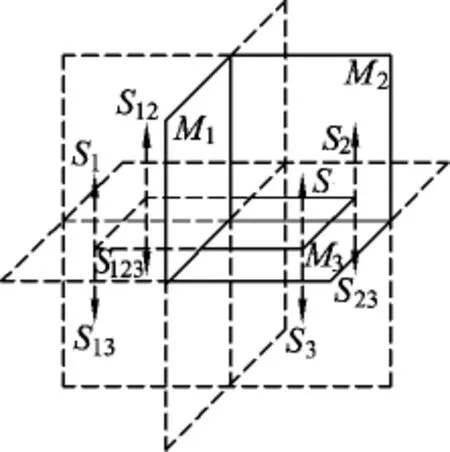
图3

为了验证结果，笔者做了实验，能很清楚看到7个像.

出题者，可能是遗漏了物体S在平面镜M3中所成的像，给出了错误的结果.

2 对互成角度2面平面镜成像规律的讨论

“再思考”一文中另一个结论：“像和被成像者关于镜面对称，既然是对称的，它们应该成对出现，成像个数就为奇数.”

平面镜成像个数一定为奇数吗？从上面的讨论可知，2面互相垂直的平面镜应该成4个像，因为经过2次反射所成的2个像重叠，所以能看到3个像.如果2次反射所成的像不重叠，那么成像个数可以是偶数个，这种情景存在吗？

图4

如图4所示，设两平面镜OM、O N镜面夹角为θ，两镜面间有一物点S，与两镜面直线相交于0点的距离为R.根据平面镜成像的特点，作物点S的像点S1、S2、S3、S4、…… 和 S1′、S2′、S3′、S4′、…….S1、S2、S3、S4、……是物体最后经 平 面 镜 OM 反 射 所 成 的 像 点；像 点 S1′、S2′、S3′、S4′、……为最后经平面镜O N反射所成的像点.

物点经过2平面镜多次反射后，成像位置在2平面镜延长线之间，则这个像即为最后成像，如图4中的像S7、S7′.如果S7、S7′不重叠，则成像为偶数个.

直接研究物点S经2平面镜反射成像个数，试过几种方法，发现问题比较复杂，很难得出一般规律.为此，换一种思路，先讨论2平面镜自身成像情况，在此基础上，再讨论物点成像个数规律.

2.1 平面镜自身成像

任意夹角θ的2平面镜，当它们之间的物点S经过2平面镜多次反射成像时，平面镜本身作为物体，经过彼此平面镜的多次反射也能成像.平面镜OM、ON之间的夹角为θ，根据平面镜成像原理，2平面镜成像如下图所示，小标号表示反射的次数.如OM1为平面镜OM经过1次反射后成的像，OM2为平面镜OM经过2次反射成的像……同理，ON1为平面镜ON经过1次反射后成的像，ON2为平面镜ON经过2次反射成的像……根据平面镜成像原理，OM2可以看作OM经过虚镜ON1反射成像，OM4可看作虚物OM2经过虚镜ON2反射成像……2平面镜经过多次反射后，成像位置在其自身延长线OA、OB之间，则为最后成像位置，因为此时的像位于平面镜背面，从这些“像”发出的光线不能射到镜面，因而不能再成像.

若L为奇数，平面镜及其所成的像将圆分为2 K＋1个圆心角为θ的区域和1个圆心角为α的区域，L＝2 K＋1.最后的K、K′区域没有重叠部分.所分区域关于角平分线CD对称，如图5所示.

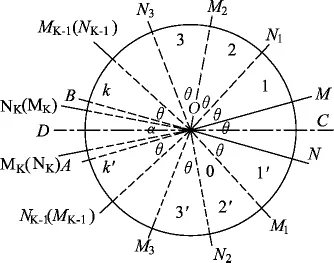
图5

若L为偶数，平面镜将圆周分为2 K个圆心角为θ的区域和1个圆心角为α的区域，L＝2 K.平面镜成像关于角平分线对称，在角平分线的2侧各形成圆心角为θ的K个区域，最后的K、K′区域部分重叠，重叠部分所对圆心角θ－α.如图6所示.

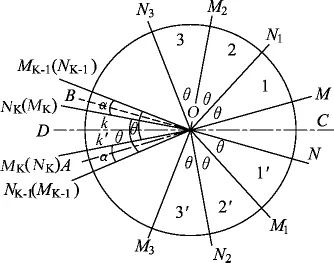
图6

2.2 物点S成像情况

物点S位于平面镜MN 之间，经过多次反射，在每个圆心角为θ的区域内成一个像.因像点位于2平面镜之间，平面镜OM、ON 的延长线OA、OB在最后的K、K′区域内，所以问题变得比较复杂.物点S最终能成几个像，关键要讨论以下2个方面.

（1）最后的K、K′区域的像SK、SK′的位置：如果SK、SK′位于2平面镜的延长线OA、OB之间，则不能再成像；如果SK、SK′位于2平面镜的延长线OA、OB之外，则能再次经平面镜反射成像.

（2）最后成的2个像会不会重叠：如果最后的2个像重叠，则成像数要减去一个.

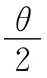
物点S在每个圆心角为θ的区域中成1个像，成2 K个像，再对K、K′区域的像SK、SK′，进行讨论.

①K区域中像点SK能再次成像SK＋1；K′区域的像SK′位于2平面镜延长线OA、OB之间，不能再成像，如图7所示.

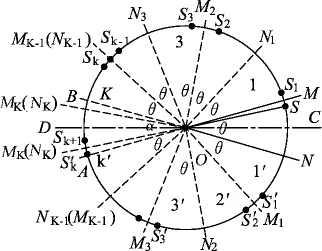
图7

像SK＋1和像SK′不可能重叠.

事实上，SK＋1、SK关于OB 对称，OMK、OMK－1关于OB对称，像点SK＋1不可能位于K′区域，所以像SK＋1和像SK′不可能重叠.

①K、K′区域中的2个像SK、SK′均能再次成像，最后2个像为SK＋1、SK＋1′，如图8所示.

图8

图9

①K区域中的像SK能再次反射成像为SK＋1，K′区域的像SK′位于OA、OB之间，不能再次成像.如图10所示.

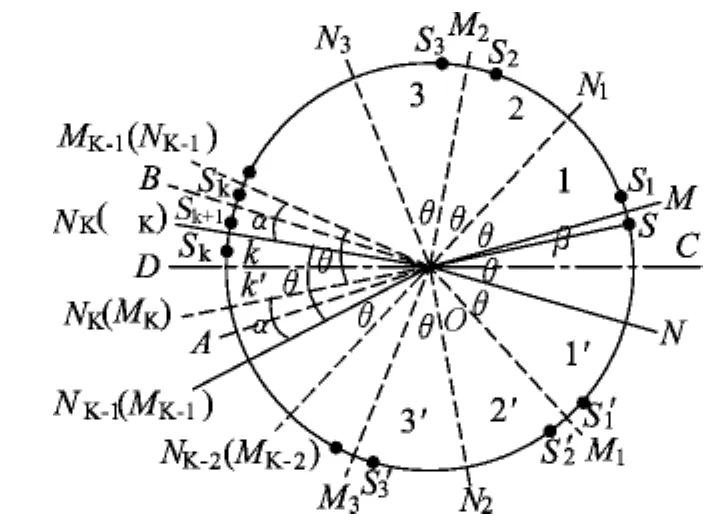
图10

若α≠0，像SK、SK不会重叠，共成2 K＝L个像.

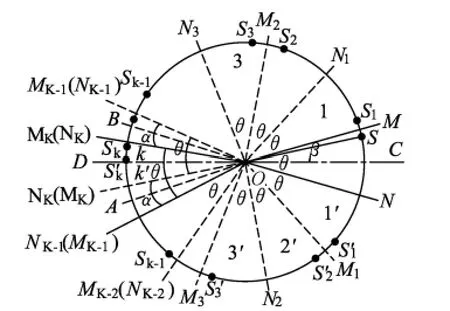
图11

这2种情况，成像个数均为L－1.

（3）成像个数列表.

表1

表1中，θ为2平面镜夹角，β为物点S与平面镜交点O的连线与2平面镜的夹角.2.4 举例L为奇数：

β≤12°，成9个像；12°≤β≤21°，成8个像.

以上是对互成角度2平面镜成像规律的讨论，如有不当之处，请各位同仁指正.