单摆周期是否存在“无穷大”——由“太空授课”引发的思考

王太军 唐忠敏

（1.西北师范大学教育学院物理教育研究所，甘肃 兰州 730070；2.西北民族大学预科教育学院，甘肃 兰州 730030）

2013年6月20日上午10时“神舟十号”航天员王亚平在“天宫一号”中给地面的师生讲授了一堂“太空物理课”（下称“太空授课”）.此次太空授课主要面向中小学生，使其了解失重条件下物体运动的特点、液体表面张力的作用，加深对质量、重量以及牛顿定律等基本物理概念和规律的理解.

太空授课中所做的物理实验，可谓奇妙无比，是在地面重力环境下无法完成的，让人尤为感慨“知道”与“看到”太不一样了.其中最为中小学生熟悉的莫过于“单摆实验”：T形支架上，细绳拴着一颗小球，这是物理课上常见的实验装置——单摆.航天员王亚平将小球拉开离支架一定角度后释放，小球却以非常慢的速度移动，并没有像在地面上那样来回摆动，随后她再拿着小球拉直细绳，轻推小球，小球即绕着支架的固定点不停地做圆周运动.

1 简谐运动物体的动力学方程

做简谐运动的物体要受到回复力的作用，其回复力F与物体相对于平衡位置的位移x成正比，方向与位移x的方向相反，即F＝－kx，其中k是比例系数.对于质量为m的小球，设在t时刻的位移是为x，加速度为a，根据牛顿第二运动定律有F＝ma＝－kx，可得

这就是做简谐运动物体的周期.

2 单摆的周期及其适用条件

单摆是一种典型的简谐运动，是一种理想化的物理模型.在地面上，实际的摆只要悬挂小球的摆线不会伸缩，悬线的长度又比球的直径大很多，或摆球的直径与悬线长相比可以忽略，再忽略各部分阻力，可认为是构成单摆的条件之一.

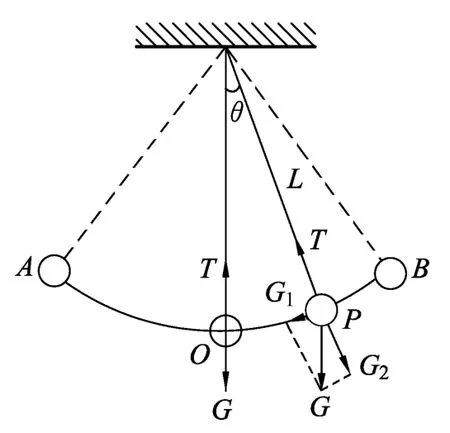
图1

当摆球静止在O点时，摆球受到的重力G和摆线的拉力T平衡，如图1所示，这个O点就是单摆的平衡位置.让摆球偏离平衡位置，此时，摆球受到的重力G和摆线的拉力T就不再平衡.在这两个力的作用下，摆球将在平衡位置O附近来回往复运动.当摆球运动到任一点P时，重力G沿着圆弧切线方向的分力G1＝mgsinθ提供给摆球作为来回振动的回复力，因此有

其中L为单摆的长度，g为地球表面的重力加速度.

表1

在单摆周期公式的推导中如果用θ代替sin θ，从理论上讲，相比直接用sinθ所产生的相对误差，随最大摆角的增大而增大.由表1可以看出，最大摆角为5°时相对误差约为0.13%，10°时约为0.51%，14°时约为1.00%.当实际摆的最大摆角为θ＜10°时，其周期与理想单摆的相对误差不超过0.5%，可近似地认为单摆的运动为简谐运动.这一结论，与用不同的方法通过对单摆模型动力学方程的解的高阶无穷小量分析所得结论基本一致［5］.

3 关于单摆的周期是否存在“无穷大”情形的探讨

根据公式（7），从纯数学的角度看，g→0时，有T→∞，似乎成立.但是这在物理意义上讲，g→0时，意味着是在近乎完全失重的条件下，而此时摆的模型中就不存在回复力了，没有回复力，其运动就不再是简谐运动，当然也就谈不上物理意义上的“单摆”了.那么，不是单摆的物理模型，而仍然用单摆模型的运动规律去讨论，显然这是不妥的，它失去了原有的意义.

地面上常用的单摆装置在“天宫一号”内，由于在近乎完全失重的状态下，没有了回复力，这时细绳并没有给球拉力，装置的钢球不再像地面上那样来回摆动，而是几乎静止在原始位置，它不构成单摆的条件，所以不能说成是“单摆的周期无穷大”，因为其前提就是错误的.若此时推动小球，相当于给了小球一个初速度，同时细绳又给小球提供拉力，细绳拉力平衡离心力，小球便绕着支架的固定点做圆周运动.这就是“太空授课”中后来我们能看到的“单摆不摆绕圆周”的有趣现象.

如果说从g→0的角度来探讨单摆的周期“无穷大”情形没有物理意义，那么据公式（7），单摆的摆长L→∞时，是否能得出单摆的周期“无穷大”？回答依然是否定的，因为公式（7）的导出过程中实际上是在把地球表面看作无限大的平面情况下得到的，而事实上地球半径的有限性使得地球表面是一个球面［6］.当摆长L很长以至可和地球半径R相比时，考虑到地球万有引力和单摆摆线的拉力的共同作用，我们必须对单摆周期公式重新进行推导［7］，得到单摆周期的修正公式为

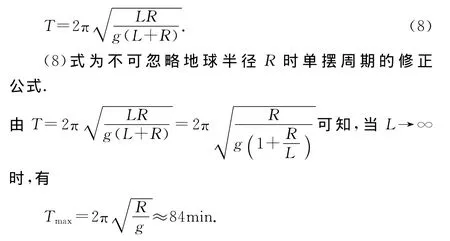
故单摆的最长周期是约84min，而不是“无穷大”.

1 周衍柏.理论力学教程（3版）.北京：高等教育出版社，2009.

2 谭志中.求大摆角单摆周期近似解的“局部常化”方法.大学物理，2005（12）：14～17

3 刘凤祥.单摆运动周期的近似解.大学物理，1999（19）：5～7

4 邵子兰.简谐运动方程的求解方法.安徽大学学报（自然科学版），1993（3）：92～94

5 吴云虎.对单摆周期测定值误差的诠释.中学物理教学参考，2004（6）：18～19

6 管习文，韦联福.单摆周期与地球半径.四川师范大学学（自然科学版），1991（4）.

7 于俊亭.对单摆周期公式若干问题的理论诠释.中学物理，2008（7）：11