基于二阶滑模与定子电阻自适应的 转子磁链观测器及其无速度传感器应用

黄 进 赵力航 刘 赫

（浙江大学电气工程学院 杭州 310027）

1 引言

自20 世纪70 年代发展至今，三相异步电机矢量控制技术已趋成熟，能够满足大部分工业需求。而精确的转子磁场定向和准确的转速观测，是保证矢量控制效果的两个最重要的因素。

为了能通过电机外部量“观测”电机内部的磁通，大部分控制方案采用的是基于数学模型的间接磁场定向矢量控制。该方法的控制性能受数学模型准确性和电机参数稳定性的影响，其中定子电阻与转子时间常数影响最大。另一方面，转速是非常重要的反馈量。传统的机械式速度传感器会带来额外的成本和安装维护方面的问题，因此无速度传感器技术一直是电机控制领域的重要研究方向。

转子磁链和转速的观测可以在只测得定子侧电信号的前提下实现[1]。将定子电流、转子磁链作为状态变量写出异步电机数学模型，在此基础上即可构建转子磁链观测器，并实现转速辨识。根据观测器构建方式的不同，可以将现有方法分为如下几类：基于状态观测器的方法，涉及人工智能的方法，以及基于模型参考自适应系统的方法。属于状态观测器范畴的有：全阶状态观测器[2]，扩展卡尔曼滤波器[3,4]，以及基于滑模理论的观测器[5-7]。全阶状态观测器对电机参数变化敏感，很难设计满足全速度稳定的反馈矩阵；扩展卡尔曼观测器计算流程复杂，大量随机参数要调试得到；一阶滑模观测器动态性能好，鲁棒性较强，但固有的抖振会影响控制性能。涉及人工智能的方法[8]一直是本行业的研究热点之一，只是受限于硬件性能，离实用化还有一定距离。标准模型参考自适应辨识[9-11]的物理意义明确，算法较简单，但同样受制于参考模型的观测精度，需要设计电机参数辨识方法加以配合。

基于滑模变结构理论的观测器对系统数学模型精确度要求较低，而且对系统的参数摄动及外部扰动具有良好的鲁棒性，所以能成为研究热点。然而，基于一阶滑模理论设计的观测器总是受困于抖振问题，实践中这一点会对系统稳定性产生不良影响。采用二阶滑模理论设计的观测器，可以在保持鲁棒性的同时削弱抖振，因此得到很多学者的关注[7]。

本文提出一种模型参考自适应理论与二阶滑模Super-Twisting 理论相结合的无速度矢量控制方案。在定子电阻与转速并行辨识的基础上，设计了一种基于二阶滑模Super-Twisting 理论的转子磁链观测器，作为速度辨识的参考模型。该观测器充分利用了辅助滑模面，因而对转子电阻变化具有良好的鲁棒性，且反应速度优于转子磁链电压模型。为了验证观测结果的准确性，文章从磁链幅值与相位两个方面进行了分析。仿真与实验结果表明，本文提出的控制方案动态性能较好，速度观测精度较高。

2 定子侧变化应对：并行定子电阻辨识

在异步电机的参数中，定、转子电阻值变化对转子磁场定向与转速估计的准确性影响最严重。定子电阻值变化是电机低速运行时控制性能不佳的主要原因。而转子电阻变化会在全速度范围影响转子磁场定向的稳定性，并且造成转速估计误差。此外，传感器的外部扰动也会影响观测结果的稳定性，进而降低整个无速度传感器驱动系统的控制性能。

定子电阻变化的影响，主要表现为定子电阻压降估计不准确，导致反电动势计算不准确。低速运行情况下，反电动势非常小，因此定子电阻压降的影响相应增大。然而，定子电阻值会随着电机温升等因素变化，导致低速运行时速度辨识算法辨识不准，进而使整个系统失稳振荡。这里先介绍一种定子电阻与转速并行辨识的方法，以应对定子侧变化对转子磁场定向与转速辨识的不良影响。

2.1 基于转子磁链的MRAS 速度观测算法

根据MRAS 原理（见图1），用电机的两个不同结构的数学模型估算同一个状态量，即可由误差设计自适应律，进而辨识转速。选择不同的状态变量，可以演化出不同结构的MRAS 辨识算法，如基于转子磁链、基于反电动势、基于瞬时无功功率等。

图1 基于转子磁链的MRAS 转速估计原理图 Fig.1 Block diagrams of rotor flux MRAS speed estimator

以转子磁链为状态变量，将电压模型（1）作为参考模型，电流模型（2）作为可调模型，可设计转 速自适应律，其中和分别表示根据电流模型和电压模型求得的转子磁链矢量。

式中 Rs——定子电阻；

Tr——转子时间常数；

Lr——转子电感；

Lm——励磁电感；

ωr——转子角速度；

误差方程写作如下形式[9]

2.2 并行转速与定子电阻辨识

分析式（3）可知，转速自适应律基于转子磁链的相位角度误差构建，而转子磁链的幅值自由度未被使用。根据文献[9]，基于转子磁链的幅值误差设计定子电阻自适应律，可实现转速与定子电阻的并行辨识。

在式（1）和式（2）基础上分别构造观测器，其中转速和定子电阻作为变量考虑。

基于转子磁链的相位角误差，构建转速自适应律，如下式表述：

相应的，基于转子磁链的幅值误差，构建定子电阻自适应律如下：

3 基于Super-Twisting 的转子磁链观测器

定子电阻只对低速运行影响较大，而转子侧参数的变化在全速度范围内都会影响控制性能。应用在永磁电机上的MRAS，通常用电机本体作为参考模型，因而能保证参考模型的准确性。前述的基于转子磁链的MRAS 速度辨识算法，采用转子磁链的电压模型作为参考模型，那么该模型观测磁链的准确性会直接影响最终参数辨识的结果。

为了得到一种更好的参考模型，本文设计了一种基于二阶滑模理论的转子磁链观测器。该观测器对转子侧的电阻变化以及扰动具有鲁棒性，且反应速度优于转子磁链电压模型。

3.1 Super-Twisting 理论

Super-Twisting 理论是滑模控制理论研究的又一成果。对于以下系统

基于Super-Twisting 理论，可以构建观测器如下[6]：

式中，ξ 是足够小的正数；λ1～λn是主滑模面的滑模增益；δ1～ δn是辅助滑模面的滑模增益；

当只有两个状态变量时，基于 Super-Twisting理论的观测器最简形式可以写成[12]

式中，λ 和δ 是滑模增益；ρ1和ρ2表示扰动。

文献[12]中基于李雅普诺夫稳定性理论，对该算法的稳定性给出了严格证明[12]。对于扰动

选取合适的λ 和δ，能使观测器的观测结果对有界扰动ρ2具有鲁棒性。

3.2 基于Super-Twisting 理论的磁链观测器设计

选取定子电流与转子磁链作为状态变量，异步电机模型可以写为如下形式：

为了便于构建基于Super-Twisting 理论的观测器，作如下变换：

式中，z1～z4为中间变量。

在式（11）中应用上述变换可得

先不考虑扰动和参数变化，并将γ 和ξ 视为确定的常数，则可根据式（10）的结构，构建基于二阶滑模理论的转子磁链观测器

e1和e2为误差值，分别定义为

3.3 扰动影响分析

考虑扰动，用ρα1和ρα2表示，将α 轴的观测器表达式重写为

转子侧参数变化和扰动带来的影响可以被折算到ρα2中，相应的，定子侧参数变化和扰动被折算到ρα1内。根据Super-Twisting 算法，对于扰动

选取合适的λ 和δ，能使观测器的观测结果对有界扰动ρα2具有鲁棒性。这里的ρα2不仅仅包含转子电阻参数扰动，它可以扩展为有界的无序扰动。

需要指出的是，该观测器对定子侧的扰动ρα1无效。由于前述并行定子电阻自适应的存在，定子电阻的变化会被自适应机构实时跟踪。此外，定子电流传感器可能存在的零漂以及低速时影响较大的死区效应，也会被定子电阻自适应机构所补偿，使得转子磁链观测器的表达式更接近实际系统，因而误差更小。

3.4 二阶滑模转子磁链观测器的实现

根据式（17）计算转子磁链，要经过一道纯积分环节，这在实验中出现直流偏置的问题。为此，用一阶低通滤波器代替纯积分环节，并对幅值和相位进行补偿[14]。采用转差频率法控制电机，取合适的补偿系数K，可由同步角速度ω1，实时计算低通滤波器的截止频率ωc（单位rad/s）。

滑模观测器普遍存在抖振问题，这是由实现滑模运动所必须的开关函数决定的。为了削弱抖振，常引入新的开关方式，以替代传统符号函数，如饱和函数和sigmoid 函数。应用替代函数要指定一个合适的边界层。边界层太厚会导致系统响应时间过长，太薄则优化效果不明显，抖振依旧很大。

与传统的一阶滑模相比，本文使用的二阶滑模方法由于辅助滑模面积分的存在，能够有效减少抖振[6]。在此基础上，本文应用开关函数优化领域的研究成果，所有采用符号函数sgn() 的场合，用饱和函数sat() 替代[13]。饱和函数的定义如下：

式中，ξ 为边界层常数，是合适的正数。

图2 给出基于Super-Twisting 理论的转子磁链观测器基本结构。

图2 基于ST 算法的转子磁链观测器结构图 Fig.2 Block diagrams of rotor flux observer based on super-twisting theory

结合定子电阻辨识模块，最终得到总体实验方案如图3 所示。

图3 总体实验方案的结构框图 Fig.3 Block diagrams of the proposed scheme

4 仿真建模分析

首先通过Simulink 建模仿真，验证本文方法的有效性。根据图4 建立间接矢量控制无速度传感器异步电机驱动系统的仿真模型。

图4 系统结构图 Fig.4 Block diagrams of the whole system

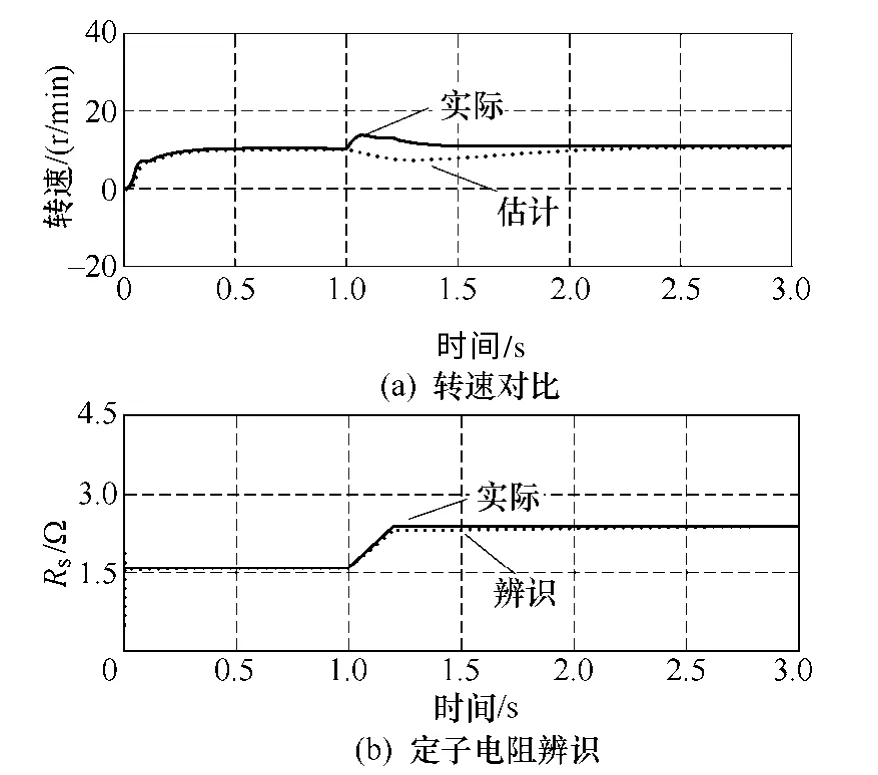
图5 启用Rs 辨识的低速（10r/min）运行 （t=1s 时切换Rs 的值） Fig.5 Low-speed operation (10r/min) with stator resistance identification (Rs changes at t=1s)

图5 是电机以10r/min 的低速运行时，定子电阻在1s 时由1.6Ω 迅速切换至2.4Ω，记录下的估计 转速、实际转速，以及给定Rs、辨识Rs波形。由图可见，Rs自适应能与转速自适应较好地并行运行，当Rs给定值变化时，Rs自适应辨识较迅速地跟上了变化，因而消去了转速的误差，使系统在低速下能稳定运行。

转子磁链电压模型中不含转子电阻，因而对转子电阻变化不敏感。为了验证本文方案对转子电阻变化的鲁棒性，在中高速变化运行时，改变转子电阻阻值进行速度辨识。如图6 所示，1.8s 时电机设定转速由150r/min 变为600r/min，2.4s 时设定转速由600r/min 变为1 000r/min。自2.0s 开始，0.2s 后转子电阻设定值由1.3Ω 迅速切换至1.7Ω。对比观测和实际转速可以发现，转子电阻的变化对本文方案的转速辨识结果也无影响。

图6 转子电阻设定变化时的无速度传感器矢量控制运行结果(150r/min→600r/min→1000r/min) Fig.6 Speed sensorless control operation with rotor resistance variation (150r/min→600r/min→1000r/min)

接下来验证二阶滑模观测器的快速性。图 7a是转速给定变化时，普通电压模型转子磁链的观测结果，而图7b 是同样条件下二阶滑模观测器的观测结果。通过比较可以得出结论，二阶滑模观测器与电压模型观测器相比，跟踪速度更快，磁链观测结果更平滑。

图7 两种不同方式在电机加速过程中的 磁链观测结果对比 Fig.7 Comparison of two methods of rotor flux observation at an acceleration process

5 实验研究

本文的实验对象为一台 15kW 的三相异步电机，具体参数参见下表。在一套变频器上实现对异步电机的无速度传感器矢量控制，实验平台如图8所示。在电机轴上装一个光电编码器，以取得实时转速数据，作为转速辨识的评判基准。同轴还加装一个转矩传感器，用于转子磁链的幅值验证，具体方法下文详述。

表 异步电机参数 Tab. Parameters of the IM

图8 实验平台实物图 Fig.8 Experimental setup

5.1 转子磁链准确性验证

与转速不同，转子磁链很难通过安装传感器来直接测得，因而不容易直观地验证磁链观测结果的准确性。转子磁链包含幅值与相位两部分信息，需要设计实验，分别验证。

文献[15]为证明其转子时间常数辨识的准确性，采用给定iq电流分量为方波，观测转速波形方法。该法可以广泛地被用于验证转子磁场定向的准确性，当转子磁场定向准确时，定子电流dq 分量之间解耦，因而控制电流id分量不变，iq分量与转矩成正比。给定电流iq分量为方波，磁场定向越准确，那么在方波转矩的作用下，转速波形越接近真正的三角波。如图9a 所示，实测的转速波形呈现较好地三角波，说明观测结果的相位较为准确。

磁链幅值观测在直接转矩控制中非常重要。当磁场定向准确时，恒幅值变换后磁链幅值ψr与转矩Te存在如下关系：

与电机同轴安装一台转矩传感器，将转矩实测波形与式（19）的转矩观测波形对比，如图9b 所示。图中实测转矩波形在转矩给定发生跳变时出现超调与振荡，这是因为电机联轴器处的橡胶圈已经老化，单靠垫片无法压紧，当转矩突变时电机与负载会有瞬间错位。系统稳态时实测波形与观测波形重合，说明转子磁链观测结果的幅值较为准确。

图9 转子磁链准确性验证 Fig.9 Accuracy verification of rotor flux

5.2 系统低速运行分析

为了验证定子电阻并行辨识的有效性，在电机的定子三相各串联一只0.5Ω/250W 的功率电阻，通过一个并联空气开关投切。为了模拟定子电阻的渐变，在每只功率电阻上再并联一台0～17Ω/3.5A 的滑动变阻器，具体接法如图10 所示。因而，定子每相电阻能可控地变化0.5Ω。实验在10r/min 的低速状况下进行。

图10 定子电阻渐变模拟 Fig.10 A circuit for variable Rs identification verification

图11 为启用Rs辨识之后记录的系统运行结果。由图中可见，人为加入的定子电阻阻值变化，会被并行Rs自适应方法有效辨识，因而保证了转速辨识的准确性，使系统能以低速稳定运行。

图11 启用Rs 辨识的低速运行（10r/min） Fig.11 Low-speed operation with stator resistance identification (10r/min)

5.3 中高速性能分析

图12 记录了电机由150r/min 到600r/min 的加速过程中，定子电流 α 分量、转子磁链以及转速的波形变化。加速过程中，转子侧电磁情况处于瞬态，而观测得到的定子电流和转子磁链波形变化较为平稳。转子磁链观测的快速性、平滑性，保证了转速估计的稳定性和准确性。整个加速过程中，电机在无速度传感器矢量控制方案下，转速误差较小，系统运行稳定。

图12 加速过程中的电流、磁链与转速观测 Fig.12 Currents,rotor flux and speed waveforms recorded at an acceleration process

6 结论

本文结合模型参考自适应理论与二阶滑模的Super-Twisting 理论，提出一种转子磁链观测和转速辨识方案，用于异步电机矢量控制。通过原理分析与实验研究得到如下结论：

（1）由于采用了并行定子电阻辨识的方法，本方案能使系统稳定运行在0.5Hz 的低速状态下。

（2）本文提出的二阶滑模转子磁链观测器，对转子参数变化具有鲁棒性，而且相比基于电压模型的传统观测器，反应速度更快。

（3）用本文提出的方案，实现一台15kW 异步电机的无速度传感器矢量控制运行，实验证明该方案磁链观测的幅值、相位均比较准确，整个系统运行稳定，控制效果较好。

[1] Vaclavek P,Blaha P,Herman I.AC drive observability analysis[J].IEEE Transactions on Industrial Electronics,2013,60(8):3047-3059.

[2] Zaky M S.Stability analysis of speed and stator resistance estimators for sensorless induction motor drives[J].IEEE Transactions on Industrial Electronics,2012,59(2):858-870.

[3] Barut M,Bogosyan S,Gokasan M.Speed-sensorless estimation for induction motors using extended Kalman filters[J].IEEE Transactions on Industrial Electronics,2007,54(1):272-280.

[4] 尹忠刚,赵昌,钟彦儒,等.采用抗差扩展卡尔曼滤波器的感应电机转速估计方法[J].中国电机工程学报,2012,32(18):152-159.

Yin Zhonggang,Zhao Chang,Zhong Yanru,et al.A speed estimation method of induction motors using the robust extended Kalman filter[J].Proceedings of the CSEE,2012,32(18):152-159.

[5] Zaky M S,Khater M M,Shokralla S S,et al.Wide-speed-range estimation with online parameter identification schemes of sensorless induction motor drives[J].IEEE Transactions on Industrial Electronics,2009,56(5):1699-1707.

[6] Solvar S,Le V,Ghanes M,et al.Sensorless second order sliding mode observer for induction motor[C].IEEE International Conference on Control Applica- tions,Yokohama,Japan,2010:1933-1938.

[7] 张勇军,孙寅飞,王京.基于单维离散滑模的模型参考自适应转速辨识方法[J].电工技术学报,2012,27(4):54-58.

Zhang Yongjun,Sun Yinfei,Wang Jing.A speed estimation algorithm based on single-manifold discrete time sliding mode model reference adaptive system[J].Transactions of China Electrotechnical Society,2012,27(4):54-58.

[8] 王耀南,陈维.无速度传感器的感应电机神经网络鲁棒自适应控制[J].中国电机工程学报,2008,28(33):92-98.

Wang Yaonan,Chen Wei.Speed sensorless neural network robust adaptive control for induction motors[J].Proceedings of the CSEE,2008,28(33):92-98.

[9] Vasic V,Vukosavic S N,Levi Emil.A stator resistance estimation scheme for speed sensorless rotor flux oriented induction motor drives[J].IEEE Transactions on Energy Conversion,2003,18(4):476-483.

[10] Jevremovic V R,Vasic V,Marcetic D P,et al.Speed-sensorless control of induction motor based on reactive power with rotor time constant identifica- tion[J].IET Electric Power Applications,2010,4(6):462-473.

[11] 尹忠刚,刘静,钟彦儒,等.基于双参数模型参考自适应的感应电机无速度传感器矢量控制低速性能[J].电工技术学报,2012,27(7):124-130.

Yin Zhonggang,Liu Jing,Zhong Yanru,et al.Low-speed performance for induction motor sensorless vector control based on two-parameter model reference adaptation[J].Transactions of China Electrotechnical Society,2012,27(7):124-130.

[12] Moreno J A,Osorio M.Strict Lyapunov functions for the super-twisting algorithm[J].IEEE Transactions on Automatic Control,2012,57(4):1035-1040.

[13] 程帅,姜海博,黄进,等.基于滑模观测器的单绕组多相无轴承电机无位置传感器控制[J].电工技术学报,2012,27(7):71-77.

Cheng Shuai,Jiang Haibo,Huang Jin,et al.Position sensorless control based on sliding mode observer for multiphase bearingless motor with single set of windings[J].Transactions of China Electrotechnical Society,2012,27(7):71-77.

[14] 何志明,廖勇,向大为.定子磁链观测器低通滤波器的改进[J].中国电机工程学报,2008,28(18):61-65.

He Zhiming,Liao Yong,Xiang Dawei.Improvement of low-pass filter algorithm for stator flux estimator[J].Proceedings of the CSEE,2008,28(18):61-65.

[15] Riveros J A,Yepes A G,Barrero F,et al.Parameter identification of multiphase induction machines with distributed windings—part 2:time-domain techniques[J].IEEE Transactions on Energy Conversion,2012,27(4):1067-1077.