属性值为区间数的多属性决策OWA 算法

焦 佳，周庆健，2

(1.大连民族学院 理学院，辽宁 大连116605;2.大连理工大学 系统研究所，辽宁 大连116024)

多属性决策是决策者在考虑多个属性的情况下，对方案集进行排序并择优的决策问题，是现代决策科学的一个重要组成部分，在当今社会诸多领域中有着广泛应用。一般说来，多属性决策可分为两个步骤:(1)获得相应决策信息，它一般包括两个方面，即属性权重和属性值;(2)通过一定方式对决策信息进行集结并对方案集进行排序和择优。在多属性决策问题中，由于决策问题的复杂性和决策者对事物判断的不确定性，决策者常常不能给出属性的精确数值，因此在描述不确定性信息时常采用区间数形式。所以属性值为区间数的多属性决策问题受到了众多该研究领域的专家及学者的关注。当前现有的针对属性值为区间数的决策方法有:可能度法、逼近理性点算法、最小偏差法、粗糙集法、概率方法和中转算法等等［1－7］。其中文献［1，5］对属性值为实数的多属性决策给出了OWA 算法，文献［2］中应用OWA算法解决了对共识语言模型的群决策问题，文献［3］给出了决策对象的优势关系与其属性值两端点的实数值之和存在等价关系的论断。

本文结合以上研究结果，对此类问题提出了一种新的更为简洁实用的决策分析方法。首先论证决策对象的优势关系与其属性值区间数的两端点数值平均值(区间中值)存在等价关系，然后将区间数的多属性决策问题转化为以区间中值为属性值的决策问题，应用OWA 算法进行方案的排序与择优，最后给出一个实例。

1 决策分析

1.1 区间数

1.2 区间数优势关系

性质2 理想点的优势关系:

由此说明在决策中，决策对象的优势关系与决策区间属性值的区间中值大小等价。

性质3 (1)当且仅当由正理想点构成的方案为最优方案时，;

(2)当且仅当由负理想点构成的方案为最优方案时，

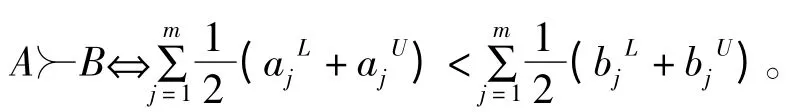
证明 (1)当U*={，，…，}为正理想点构成的决策方案时，有，则若A≻B，则，有即;同理可证(2)成立。

综上可知，属性值为区间数的多属性决策对象排序时，决策对象优势关系大小与其属性值区间的区间中值大小等价。从而可以把对区间数的排序问题转化为对区间中值的排序，这种方法比较简洁方便。

1.3 多属性决策的有序加权平均算法(OWA 算法)

对于某一多属性决策问题，设X=(x1，x2，…，xn)为方案集，U=(u1，u2，…，um)为属性集。

定义6 设算子OWA:Rn→R，若OWAω(α1，α2，…，αn)=，其中ω=(ω1，ω2，…，ωn)是加权向量，ωi∈［0，1］，且=1，bj是一组数据(α1，α2，…，αn)中第j 大的元素，R 为实数集，则称函数OWA 是有序加权平均算子，也称OWA 算子。在此我们采用权重ω=(ω1，ω2，…，ωn)的一种常用选择:

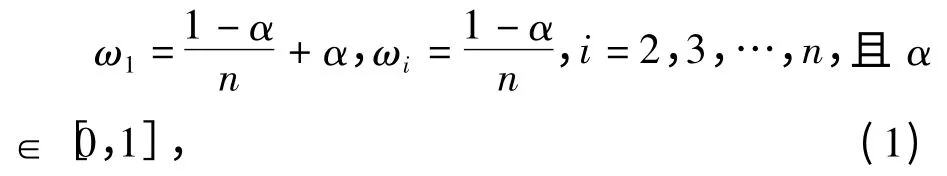
这样就可以根据多属性决策的OWA 算法进行方案集的排序和择优，进而解决属性值为区间数的多属性决策问题。

2 多属性决策的OWA 算法决策步骤

综上分析，我们应用OWA 算法解决属性值为区间数的多属性决策问题的步骤如下:

步骤1 由决策对象优势关系大小与其属性值区间的区间中值的大小等价，我们把原始决策矩阵中的每个区间［aL，aU］用区间中值来等价替换，这样原始的有区间数构成的决策矩阵就转换成由实数构成的决策矩阵A=(aij)。

步骤2 将决策信息的原始数据构成的决策矩阵A=(aij)规范化，得到规范化矩阵R (rij)。常见的属性类型有效益型和成本型，其中效益型属性是越大越好，成本型属性是越小越好。设I1，I2分别表示效益型和成本型属性的下标集，为消除不同物理量纲对决策结果的影响，可对原始属性值作如下规范化处理:

这样就得到规范化矩阵R=(rij)。

步骤3 应用式(1)中给出的方法确定加权向量ω=(ω1，ω2，…，ωn)，利用OWA 算法对各方案xi进行集结，求得其综合属性值zi(ω)=OWAω(ri1，ri2，…，rim)=，且bij是ri1，ri2，…，rim中第j 大的元素。

步骤4 按zi(ω)的大小对方案进行排序和择优，确定最优方案。

3 实例分析

某投资银行拟对某市4 家企业(方案)xi，i=1，2，3，4 进行投资，抽取下列5 项指标(属性)进行评估:u1表示产值(万元)，u2表示投资成本(万元)，u3表示销售额(万元)，u4表示国家收益比重，u5表示环境污染程度。投资银行考察了上年度4 家企业的上述指标情况，所得评估结果见表1，其中，投资成本、环境污染程度为成本型，其他3 个为效益型，属性权重按式(1)取定，试确定最优投资方案［1］。

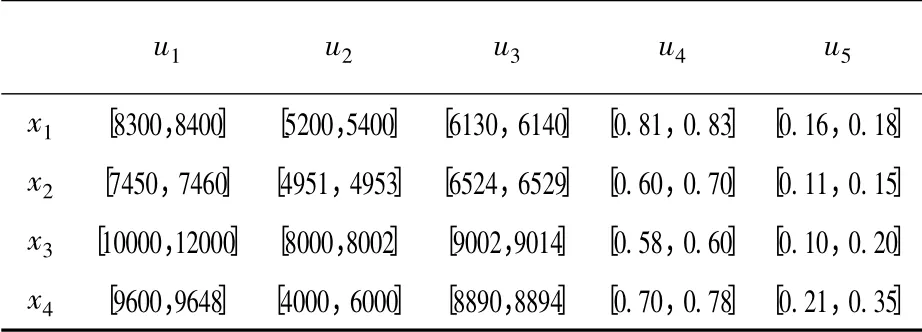
表1 决策矩阵表格

步骤1 把原始决策矩阵中的每个区间数用区间中值来等价替换，得到由实数构成的决策矩阵:

步骤2 将A=(aij)按照式(2)(3)规范化得矩阵

步骤3 按属性权重式(1)，结合问题实际意义设α=0.6，则ω=(0.6，0.1，0.1，0.1，0.1)，利用OWA 算子对每个方案xi，i=1，2，3，4 的属性值进行集结，求其综合属性值zi(ω)，i=1，2，3，4，则

步骤4 按综合属性值zi(ω)，i=1，2，3，4 的大小对各企业进行排序x3＞x2＞x4＞x1。

故可看出最优企业是x3，该投资银行可选择第3 家企业。

4 结 语

属性值为区间数的多属性决策问题是现代决策科学的重要组成部分。本文针对此类多属性决策进行了深入研究，主要做了如下3 个方面工作:(1)首先论证决策对象的优势关系与其属性值区间数的区间中值存在等价关系;(2)将区间数的决策问题转化为以区间中值为属性值的决策问题;(3)应用有序加权平均算法进行方案集的排序与择优。通过验证表明，本文方法实用可行，较好地解决了属性值为区间数的多属性决策问题。

［1］徐泽水. 不确定多属性决策方法及应用［M］. 北京:清华大学出版社，2004.

［2］ BORDOGNA G，FEDRIZZI M，PASI G. A linguistic modeling of consensus in group decision making based on OWA operators［J］. IEEE Transactions on Systems，Man and Cybernetics，1972，27:126 －132.

［3］刘健，刘思峰. 属性值为区间数的多属性决策对象排序研究［J］. 中国管理科学，2010，18(3):90 －94.

［4］樊治平，胡国奋. 区间数多属性决策的一种目标规划方法［J］. 管理工程学报，2000，14(4):50 －52.

［5］徐泽水. 几类多属性决策方法研究［D］. 南京:东南大学，2002.

［6］JAHANSHAHLOO G R，LOTFI F H，IZADIKHAH M.An alforithmic method to extend TOPSIS for decision －making problems with interval data［J］. Applied Mathematics and Computation，2006，175(2):1375 －1384.

［7］尤天慧，高美丽. 一种考虑决策者风险偏好的区间数多属性决策方法［J］. 运筹与管理，2012，21(1):70－74.