总体最小二乘的扰动分析*
王乐洋
1)东华理工大学测绘工程学院,南昌 330013
2)江西省数字国土重点实验室,抚州344000
1 引言
总体最小二乘(total least squares,TLS)自Golub 和Van Loan[1]于1980年首次从数值分析的观点进行分析并为之定名以来在算法和应用方面得到了广泛的研究[2-5]。在总体最小二乘解的性质方面也有大量的研究,如总体最小二乘与最小二乘在解、残差、数据拟合的改正数以及近似子空间的内部联系[2],加权总体最小二乘问题的等价解集以及加权总体最小二乘解与加权最小二乘问题解之间的关系[6],总体最小二乘解集、最小二乘解集以及与极小范数解之间的差异等等[7]。但是,关于总体最小二乘的扰动分析研究不是很多,主要有总体最小二乘问题的统计特性和解扰动的上限值的研究[2];基于标度总体最小二乘解存在且唯一的Golub-Van Loan 条件下的标度总体最小二乘问题的扰动分析[8]等。因为总体最小二乘及标度总体最小二乘问题并没有最小二乘问题那样简单的范数表示的条件数,而分量条件数考虑了数据分量之间的关系,所以标度总体最小二乘问题的扰动分析是基于分量条件数的,而且由标度总体最小二乘问题的条件数可以得到总体最小二乘问题的条件数[8]。从数值分析的角度进行扰动分析研究一般具有简单、直接的优点,但是,从测量平差和数值分析的角度进行总体最小二乘、最小二乘及数据最小二乘解之间的扰动分析及其关系的研究鲜有报道。标度总体最小二乘扰动分析的研究所给出的条件数是关于整个标度总体最小二乘问题的,本文将从测量平差问题的法方程出发,从数值分析的角度,以系数矩阵条件数的定义为基础并以奇异值分解为工具详细推导总体最小二乘、最小二乘及数据最小二乘解的扰动分析公式及三者之间的关系。
2 最小二乘的扰动分析
2.1 普通最小二乘的扰动分析
线性估计模型为

式中,A∈Rm×n(m >n)为列满秩系数矩阵;X∈Rn×1为待估计参数;b∈Rm×1为观测值。
当系数矩阵A 不含有误差时,为LS 估计,法方程为

式中,N=ATA(非奇异),L=ATb
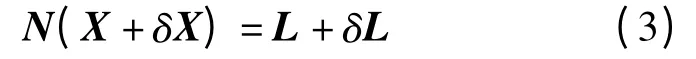
式中,δL=AT(δb)。

当NX=L≠0 时

所以
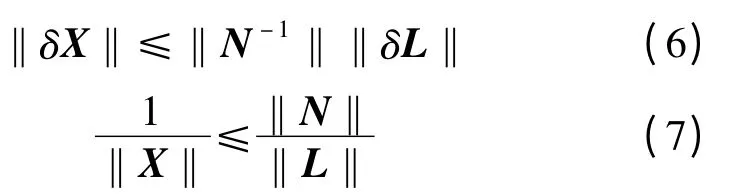
从而有

若矩阵N 为非奇异矩阵,则其条件数的定义为[9,10]

式中,‖·‖p表示矩阵的p 范数,p 取1、2 或∞。
式(8)说明:当观测值b 存在相对误差(或扰动)时,将会引起LS 解的相对误差,该相对误差的上界是常数项‖δL‖/‖L‖的‖N‖‖N-1‖(即cond(N))倍,所以解的相对误差的大小与条件数cond(N)的大小有关;当系数矩阵病态(cond(N)≫1,即条件数相对较大)时,条件数cond(N)将对解的相对误差起到放大作用。
2.2 数据最小二乘的扰动分析
线性估计模型如式(1)所示,当系数矩阵A 含有误差而观测值b 不含有误差时的LS 估计称为数据最小二乘(data least squares ,DLS)估计[11],法方程如式(2)所示。设法方程系数矩阵N 的误差(或扰动)为δN,式(1)的DLS 解为,系数矩阵N 的误差(或扰动)δN 引起的解的扰动为,模型精确解为X。
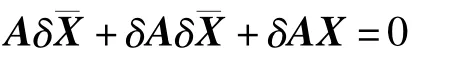
在上式两端同乘以AT得

数据最小二乘的扰动法方程为

即

所以
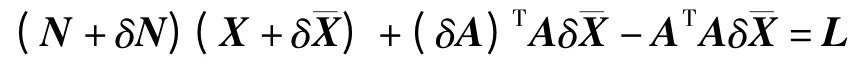

式中,δN=(δA)TδA,δA 为系数矩阵A 的误差(或扰动)。

所以有
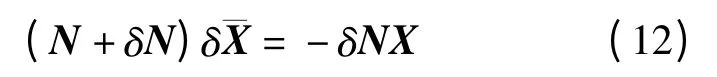
根据如下定理[10]:
如果‖B‖<1,则I±B 为非奇异矩阵,且有估计

式中,‖·‖是矩阵的算子范数。
设‖N-1‖‖δN‖<1,N+δN=N(I+N-1δN)为非奇异矩阵[9],且有
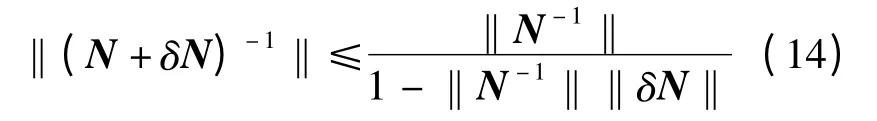
由式(12)得
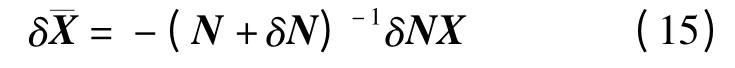
所以有

式(16)说明:如果条件数cond(N)(‖N‖‖N-1‖)越大,则系数矩阵N 的微小相对误差‖δN‖/‖N‖将会引起解的相对误差‖就越大,也就是对系数矩阵的相对误差‖δN‖/‖N‖放大了‖N‖‖N-1‖倍。
2.3 观测值与系数矩阵都存在误差(或扰动)时的最小二乘扰动分析
线性估计模型如式(1)所示,当系数矩阵A 和观测值b 同时含有误差时,最小二乘(LS)估计的法方程为式(2)所示,设法方程系数矩阵N 的误差(或扰动)为δN,观测值b 的误差(或扰动)为δb,δN 和δb 引起的解的扰动为,模型精确解为X。

在上式两端同乘以AT得

扰动法方程为
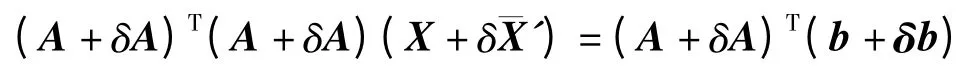
即

所以


式中,δL=δATδb。

将式(17)展开结合式(2)得

对式(19)两端取范数得

即


当δN 足够小时,有‖N-1‖‖δN‖<1,则

由式(2)得
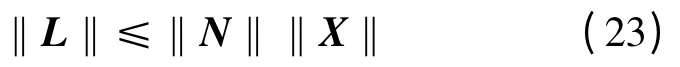
即

由式(22)和(24)得
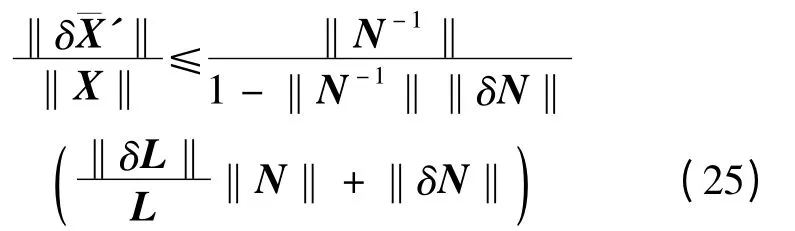
即
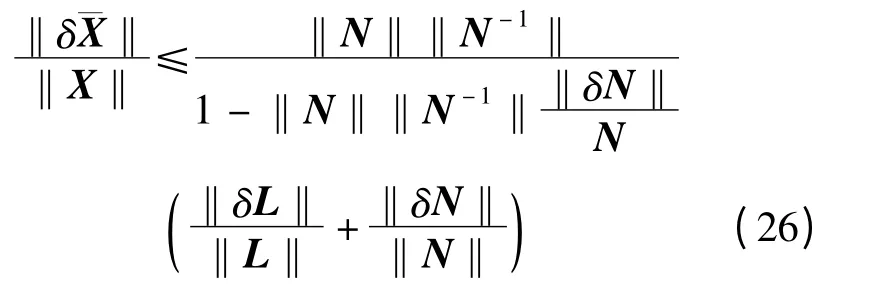
由式(26)可以看出:当系数矩阵A 和观测值b同时含有误差(或扰动)δA 和δb 时,最小二乘解LS的相对误差是由两部分引起的,即观测值的相对误差‖δL‖/‖L‖和法方程系数矩阵的相对误差‖δN‖/‖N‖两部分引起的;当系数矩阵是病态矩阵时,条件数非常大,将会对观测值的相对误差‖δL‖/‖L‖和法方程系数矩阵的相对误差‖δN‖/‖N‖起到放大作用,即引起LS 解的极大变化(或扰动),也就是说‖δL‖/‖L‖和‖δN‖/‖N‖相同的条件下,条件数cond越大,LS 解的相对误差也越大。
3 总体最小二乘的扰动分析
线性估计模型如式(1)所示,当系数矩阵A 和观测值b 同时含有误差时的估计为总体最小二乘(TLS)估计,法方程为[2]
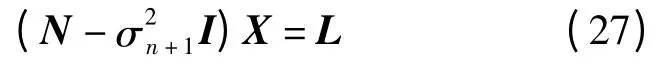
式中,N=ATA(非奇异),L=ATb,σn+1为增广矩阵[A b]的最小奇异值,即有如下奇异值分解
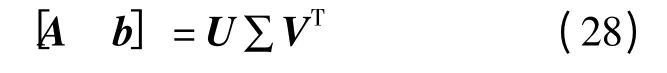
式中,U=[U1U2],U1=[u1,…un],U2=[un+1…um],ui∈Rm×1,UTU=Im;
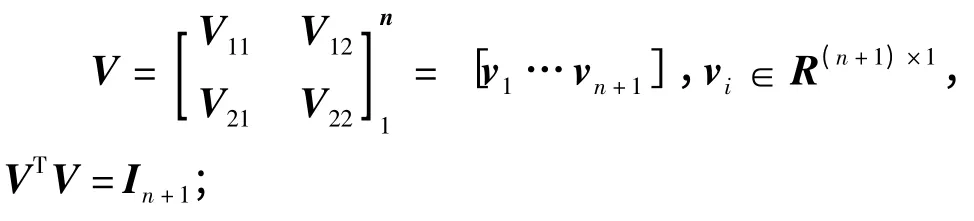
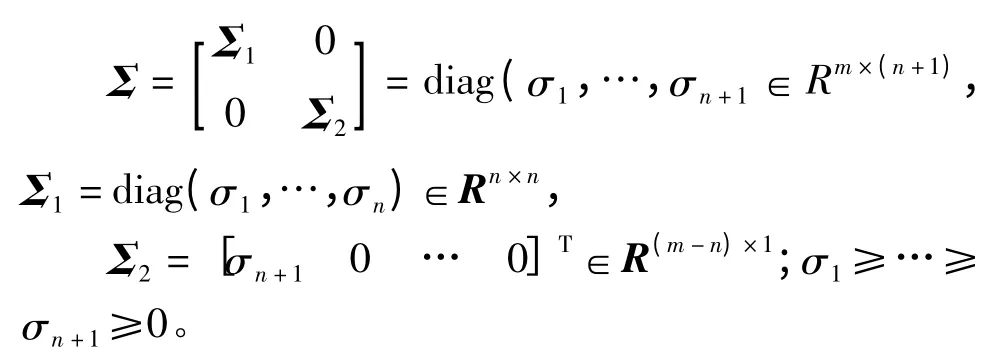
设法方程系数矩阵N 的误差(或扰动)为δN,观测值b 的误差(或扰动)为δb,式(1)的TLS 解为,δN 和δb 引起的解的扰动为,模型精确解为X,扰动法方程两边舍掉一次扰动项ATδAX、ATδAδX、(δA)TAX、(δA)TAδX、2σn+1δσn+1X、2σn+1δσn+1δX、ATδb 和(δA)Tb,则
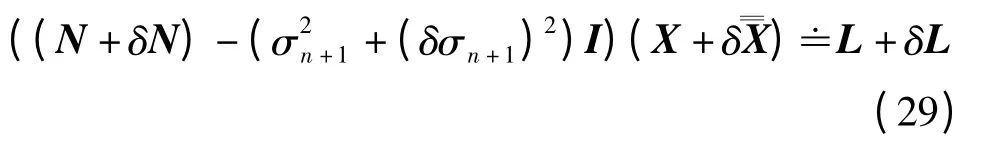
式中,δL=δATδb,δσn+1是增广矩阵[δA δb]的最小奇异值。

将式(29)展开结合式(27)得
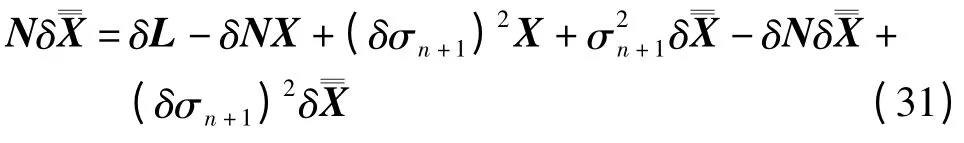
将式(31)两端同乘以N-1得
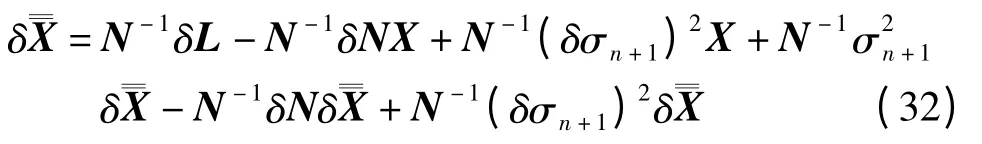
将式(32)两端取范数得
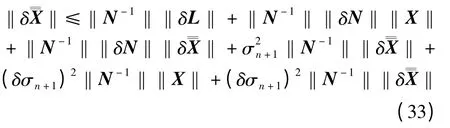
即

以矩阵的2-范数(谱范数)进行研究,则有[9]

式中,λATA=λN为矩阵ATA(即N)的最大特征值。
对系数矩阵A 进行奇异值分解得[2,10]

式中,U'=[U'1U'2],U'1=[u'1…u'n],U'2=[u'n+1…u'm],u'j∈Rm×1,U'TU'=Im;
V=[v'1… v'n],v'i∈Rn×1,V'TV'=In;Σ'=diag(σ'1,…,σ'n)∈Rm×n;σ'1≥…≥σ'n≥0。
因为矩阵A 的非零奇异值是矩阵ATA(即N)的非零特征值的正平方根,所以结合式(36)得

根据奇异值交织定理得[2,12]
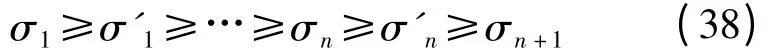
因此
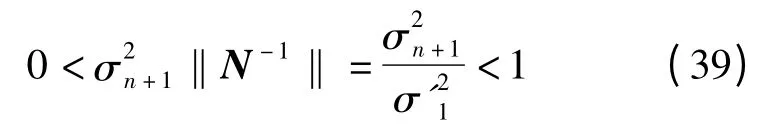
假设扰动足够小,则有

所以


在式(43)两边同除以‖X‖得

由式(27)得
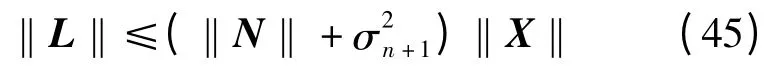
即

由式(44)和(46)得
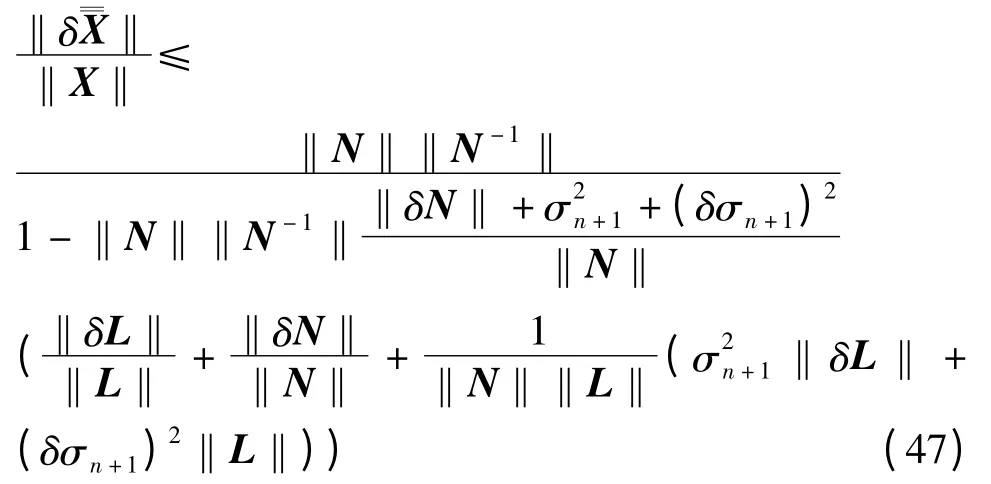
由式(47)可以看出:当系数矩阵A 和观测值b同时含有误差时的总体最小二乘(TLS)解的相对误差是由三部分引起的,即观测值的相对误差‖δL‖/‖L‖、法方程系数矩阵的相对误差‖δN‖/‖N‖以及系数矩阵和观测值组成的增广矩阵的扰动当系数矩阵病态时,条件数cond(N)(‖N‖‖N-1‖)非常大,将会对观测值的相对误差‖δL‖/‖L‖和法方程系数矩阵的相对误差‖δN‖/‖N‖以及增广矩阵的扰动起到放大作用,即引起TLS 解的极大变化(或扰动),也就是说在‖δL‖/‖L‖、‖δN‖/‖N‖和(δσn+1)2‖‖L‖相同的条件下,条件数cond(N)(‖N‖‖N-1‖)越大,TLS 解的相对误差也越大。
同时,式(47)是前面各种最小二乘(LS)扰动分析的概括(统一)形式,具体为:
1)当系数矩阵不含误差且没有扰动,仅观测值含有误差(或扰动)时,进行LS 估计,‖δN‖=0,,则式(47)变为式(8);
2)当观测值不含误差且没有扰动,仅系数矩阵含有误差(或扰动)时,进行LS 估计(DLS 估计),‖δL‖,则式(47)变为式(16);
3)当观测值和系数矩阵都含有误差(或扰动)时,进行LS 估计,,则式(47)变为式(26)。
4 结束语
在实际参数估计问题中,一般来说数据采样大小、模型化及测量等原因会引起系数矩阵的误差,而总体最小二乘方法是可以同时顾及观测值和系数矩阵误差的有效的数据处理方法,因而在参数估计中得到广泛的研究和应用。本文从数值分析的角度出发,以系数矩阵条件数的定义为基础并以奇异值分解为工具详细推导了总体最小二乘、最小二乘及数据最小二乘解的扰动分析公式,通过对比分析发现总体最小二乘扰动分析公式是各种最小二乘扰动分析公式的概括(统一)形式。
1 Golub G Hand and Van Loan C F.An analysis of the total least squares problem[J].SIAM J Numer Anal.,1980,17:883-893.
2 Van Huffel S and Vandewalle J.The total least squares problem:Computational aspects and analysis[M].SIAM,Philadelphia,1991.
3 Van Huffel S(Ed.).Recent advances in total least squares techniques and errors-in-variables modeling[M].SIAM,Philadelphia,1997.
4 Van Huffel Sand Lemmerling P(Eds.).Total least squares and errors-in-variables modeling:Analysis,algorithms and applications[M].Dordrecht:Kluwer Academic Publishers,2002.
5 王乐洋.总体最小二乘性质研究[J].大地测量与地球动力学,2012,(5):48-52,57.(Wang Leyang.Research on properties of total least squares estimation[J].Joural of Gesdesy and Geodynamics,2012;(5):48-52,57)
6 魏木生,陈果良.加权总体最小二乘问题的解集和性质[J].高校应用数学学报A 辑,1994,9(3):304-311(Wei Musheng and Chen Guoliang.Solution sets and property for weighted total least squares problem[J].Applied Mathematics-A Journal of Chinese Universities,1994,9(3):304-311.)
7 刘永辉,魏木生.TLS 和LS 问题的比较[J].计算数学,2003,25(4):479-492(Liu Yonghui and Wei Musheng.On the comparision of the total least squares and the least squares problems[J].Mathematica Numerica Sinica,2003,25(4):479-492.)
8 Zhou Liangmin,et al.Perturbation analysis and condition numbers of scaled total least squares problems,[J]Numer Algorithms:2009,51:381-399.
9 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004(Zhang Xianda.Matrix analysis and applications[M].Beijing:Tsinghua University Press,2004.)
10 易大义,沈云宝,李有法.计算方法(第二版)[M].杭州:浙江大学出版社,2002(Yi Dayi,Shen Yunbao and Li Youfa.computational method(Second Edition)[M].Hangzhou:Zhejiang University Press,2002.)
11 Paige C C and StrakoŠ Z.Scaled total least squares fundamentals[J].Numerische Mathematik,2002,91:117-146.
12 Thompson R C.Principal submatrices IX:Interlacing inequalities for singular values of submatrices[J].Linear Algebraappl.,1972,5:1-12.

