承压井与非承压井水位潮汐效应及其定量分析*

刘序俨 郑小菁 陈 莹 张清秀 王 林

(福建省地震局，福州 350003)

1 引言

利用井水位观测值可以获取含水层压力水头在区域应力作用下的动态特征，进而利用井水位观测值直接分析或反演强震孕育区构造应力场变化，为强地震孕育过程提供区域构造活动程度和地震孕育短临阶段前兆异常信息等。

在地震监测台网中，除了符合地下流体观测规范的承压观测井外，还有一部分非承压观测井。尽管非承压井的水位观测会受到各种环境影响，水位观测值不能完全反映固体介质变形的特征，但仍有一些非承压井对应力应变有良好的响应能力。

对承压井水位潮汐效应，文献［1，2］作了阐述，而对于非承压井水位潮汐效应，很少有文献涉及。承压井与非承压井的井潮机理有何不同，又如何对两者的承压性作定量分析，是本文讨论的主要问题。

2 承压井与非承压井

非承压井是相对于承压井而言的，如果两个隔水层之间的含水层中的水是不封闭的，具有自由表面，为无压水［1］，钻透该含水层的井称为非承压井，由于非承压井是不封闭的，非承压井水位易受到潜水、大气降水、凝结水、地表水的影响，而潜水具有季节性变化特点，因此非承压井水位受季节性影响较大。

2.1 承压井水位的井潮机理

设静水压强为P，设θ 为承压地下水这个由含水层所组成的孔隙介质在该静水压力下所发生的体应变，对于理想的水平层状承压含水层，假定各层的力学性质是各向同性的理想弹性体，考虑在承压含水层中，单位体积多孔介质中流体含量的改变量为零［3］。根据线弹性理论［3，4］，承压含水层的孔隙压(静水压)变化只与平均应力变化成正比，即:

对于含水层这种弹性孔隙介质，根据文献［2，6］，由静水压力P 所产生的弹性孔隙介质的体应变为

式中n 为含水层的孔隙度，Bs与Bw分别为岩石和流体的体积模量。设，k 称为弹性孔隙介质的压缩系数，由式(2)可得

当嵌套在岩体中的承压含水层受到静水压力P作用时，根据流体静力学基本方程［6－8］可得井水位h 与体应变θ 的关系式为

当n=0 时，由式(2)可知，表示体应变完全是由岩体所引起，此时当n=1 时，表示体应变完全由流体所引起，此时实际的观测井，孔隙度既不等于0，也不等于1，而它鉴于两者之间。因此有，考虑到在地壳中岩石的体积压缩模量Bs为(0.44 ～1)×1011Pa，水的Bw为2.2 ×109Pa［6－8］，并顾及到水的重度ρg=104Pa/m，则有，式中ρgk 称为井水位的格值，其倒数称为井水位的放大倍数。当θ=10－9时，则有0.22 mm ＜h ＜(4.4－10)mm，表明含水层发生微小体应变时，承压井水位会发生可以观测到的显著变化，因此更确切地说，承压井水位是一个水压计。

2.2 非承压井水位观测原理

设井孔的半径为r，在含水层体应变为θ 的条件下，井水位变化幅度为h，含水岩体的有效体积为v，则

亦即

式(6)表明，在体应变不变的前提下，h 与v 成正比，与井孔半径的平方成反比。井孔半径越小，井水位变化幅度越大，反之亦然。这样，对于纯体积变化所引起的井水位变化，与体应变的关系不是一个确定的常数，虽然式(6)中的像式(4)的样是放大倍数，但不是一个常数，并且无法事先获知有效水体积v，因此，也就无法由井水位变化值求出体应变值。由于井水位的变化幅度h 取决于有效水体积，当θ=10－9，r=10 cm，h=1 cm 时，由式(6)可求得，这个有效水体积相当于一个边长为67.98 米的立方体的水体积。只有在有效水体积v 大于上述数值的前提下，这口井孔半径为r=10 cm 的井水位才能在体应变为10－9的激励下，变化达到1 cm 以上。当然，在有效水体积不变的前提下，孔径越小，井水位变化越大。对于非承压井而言，钻孔半径越小，观测到的井水位变化幅度越大，但由于有效水体积是无法得知的，我们无法求得非承压井水位的放大倍数。

3 井水位体应变固体潮与气压效应

一般来说，引起含水层压力水头变化的原因有两种:含水层内水量的增减和含水层应力应变的变化。对于封闭较差的含水层主要是第一种情况，例如降雨和同层抽水都可以引起含水层压力水头发生变化。对于封闭性良好的含水层主要是第二种情况，若封闭含水层内只有一口井，其压力水头的变化只取决于含水层所受的应力应变的变化。当然，实际上由于含水层的封闭性不可能是完全理想的，所以，许多水井含水层压力水头的变化是两种原因的综合。如果把含水层系统的力学性质看作是完全弹性介质，在水力学性质上是均匀的可渗透的含水层，那么根据地球固体潮理论结合地下流体动力学理论可知，对于水文地质中典型的承压含水层模式，其内的一口井径不大的完整井，可以求出水井水头与固体潮体应变之间的关系，可以推导出由于体应变所引起的承压井水位涨落表达式。除了固体潮体应变外，由其他外因所引起的井水位涨落表达式，例如气压所引起的表达式，一般很难给出理论表达式的。

考虑二阶天体起潮力位V2占整个起潮力位的绝大部分，并考虑到近地表的泊松比v=0.25［9］，可得近地表的固体潮体应变表达式为

式中h2与l2为二阶勒夫数与志田数，分别为0.614 4与0.083 2［10］。将式(7)代入式(4)，由体应变所引起的水位涨落为

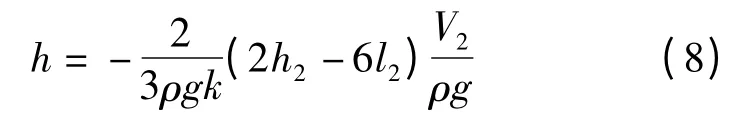
虽然式(8)表明了承压井的井水位变化与体应变θ 及含水层孔隙介质的压缩系数k 有关，即使对于非承压井而言，其井水位变化在一定程度上也是与体应变有关，不过是与部分体应变有关的。因此，凡是能程度不同地记录到体应变固体潮的承压井和非承压井观测系统皆可用来对体应变固体潮进行观测研究。利用井水位观测资料，采用维尼迪柯夫调和分析方法可能获得在频域范围内井水位观测资料与体应变固体潮理论值的振幅与相位滞后。如果采取的体应变理论模型越接近于含水层的体应变情况，则振幅比就越接近于式(4)中的，相位滞后就越接近于零。通常地质沉淀物是随深度加深而减小的，这有助于增加潮汐影响的程度，并且隔水层的渗透性一般也随深度加深而减小，这样深部含水层就严格地接近于理想的承压状态［11］，这就是为什么在深井中会产生较大的地球潮汐。同时，由于深井不易受到地表水的渗透，因此，井水位的上升或下降，可以看做是含水层孔隙介质的压缩或膨胀。所以，承压井水位不但可以作体应变观测，而且可用来捕捉地震前兆。由于非承压井易受地表水、降水的影响，因此，在井水位出现较大幅度的变化时，要对井孔附近的用水情况进行调查分析，但叠加在井水位非线性变化背景上的固体潮变化信息却含有地壳特性变化信息。这种特性变化可由体应变观测曲线的畸变和维尼柯夫调和分析获得的井水位观测资料的振幅比(潮汐因子)取得。

4 观测井水位承压性定量比较

设hi与Fi分别为井水位与天体起潮力在时刻i 时的观测值与加速度理论值。设Δhi=hi－hi－1，ΔFi=Fi－Fi－1，hi根据井水位整点值观测资料进行差分得到，Fi根据重力固体潮理论值Zi、东西向与南北向倾斜固体潮理论值xi与yi采用［12，13］:

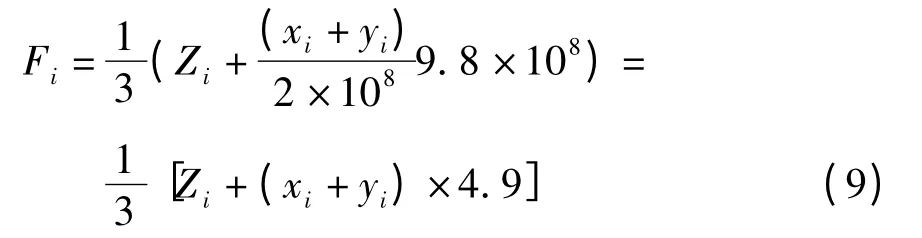
计算得到。式中Fi为天体起潮力在x、y、z 方向对单位质量的加速度的平均值，其中Z 的量纲为10－8ms－2，xi与yi的量纲为ms(10－3角秒)。采用泉州与海口观测井2011年1月的整点值获得的Δhi与ΔFi的相关系数见表1。

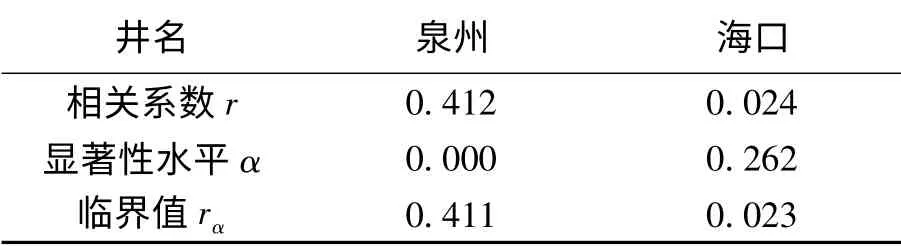
表1 泉州与海口观测井Δhi 与ΔFi 的相关系数(自由度f=741)Tab.1 Correlation coefficient between Δhi and ΔFi at Quanzhou and Haikou wells

表1 中的显著性水平表明，在给定显著性水平为α 时，检验零假设H0:ρ=0 的否定域为由确定，rα为在给定显著性水平α时的两变量的母体相关系数ρ=0 的临界值［14］。在给定自由度的前提下，α 越小，rα值越大;自由度越大，rα值越小。2011年1月，福建泉州井与海南海口井的差分数据的自由度f=741。对泉州井，当取α=0.000 1，rα＜0.412，此时，在显著性α=0.000 1水平上，可认为泉州井的井水位与天体起潮力为显著相关的。对海口井，仅有在取α=0.262 时，r 才大于rα(0.023)，因此α ＞0.262，在显著性水平＞0.262 水平上，可认为海口井的井水位与起潮力的相关性是不显著的。一般作检验时，取α=0.05 或0.01 对相关系数与母体的相关系数ρ=0 作差异显著性检验。当α 比0.01 越来越小，rα则越来越大，则r 与ρ=0 的差异性越来越大，则相关性越来越强;当α 比0.05 越来越大，rα则越来越小，则r 与ρ=0 的差异性越来越小，则相关性越来越弱。由Δh=a+bΔF 作回归分析，可分别得泉州与海口观测井的基线差a 与回归系数b(表2)。

表2 中的a 的量纲为m，n 的量纲为m/Pa。需要说明的是，根据式(1)，井水位的静水压力是与天体起潮力的平均值成正比但反号。因此，井水位与静水压力的表2 中的回归系数应为正。当静水压力增加时，井水位上升，反之为负。回归系数b表示当静水压强增加1 个单位时，井水位上升的幅度。因此b表征了井水位对静水压强的响应能力。依上文，只有当含水层为封闭时，天体起潮力传递给含水层流体中的静水压强才能达到极大值，这就是为什么承压井水位对体应变响应最为灵敏的原因。b 就可作为这种灵敏度。从表2 可看出，泉州观测井的b 值比海口观测井的约大7 倍。因此，采用相关与回归方法，可对观测井的承压程度进行定量比较。

表2 泉州与海口水井的回归系数Tab.2 Regression coefficient between Δhi and ΔFi at Quanzhou and Haikou wells

5 认识与讨论

在基于承压井和非承压井特征分析的基础上，着重指出承压井的含水层中的地下水是封闭、不自由的，由于受到静水压强的作用，承压井中的水为承压水;而非承压井的含水层中的地下水是自由的，没有受到静水压强的作用，因而其中的地下水是非承压水，承压井的含水层的体应变与井水位变化皆为含水层对静水压强的两种不同形式的响应形式。其水位变化所引起的钻孔中水的体积的增减并不等于含水层胀缩所导致的那部份体积变化，但钻孔中井水位变化所引起的压强变化却等于含水层中静水压强的变化，从这个角度看，承压井的井水位变化是一个动力学问题，其放大倍数是一个与含水层岩体与流体的体积模量与该含水层的孔隙度有关的常数。而非承压井的井水位变化是一个几何学问题，其井水位变化纯粹为地下水在体应变作用下在井孔中的响应罢了。井孔中的水的体积的变化反映了含水层的体应变，其变化的幅度取决于井孔的大小，同时又取决于有效水体积。由于有效水体积变化无法得知的，因而我们无法求得非承压井水位的放大倍数。在这里要特别指出，对承压井与非承压井问题的阐述，是建立在层状岩层的基础上的，特别是对第四系砂砾岩孔隙含水层而言的;对基岩裂隙含水层则不完全符合。由于裂隙发育的不均一性，对一定深度的非承压观测井而言，其井水位多具有一定的承压性。

无论是承压井还是非承压井，只要它们能清晰地记录到固体潮，即使在降水、渗流、气温、气压等干扰下，仍然能在井水位出现在大幅度的线性或非线性变化的背景上记录到叠加在其上的固体潮体应变，仍可进行体应变观测。图1 与图2 分别为2011年1月份泉州与海口井水位观测曲线图，从曲线图可发现，泉州井为规则的半日波，而海口井则为规则的日波，这是与它们的潮港类型相吻合的，从厦门到温州沿海的潮港为规则的半日波潮港类型，而海口沿海则为规则的日波潮港类型，说明沿海井水位都程度不等地受到海潮影响，但不管怎样，它们都是由天体起潮力所引起的。

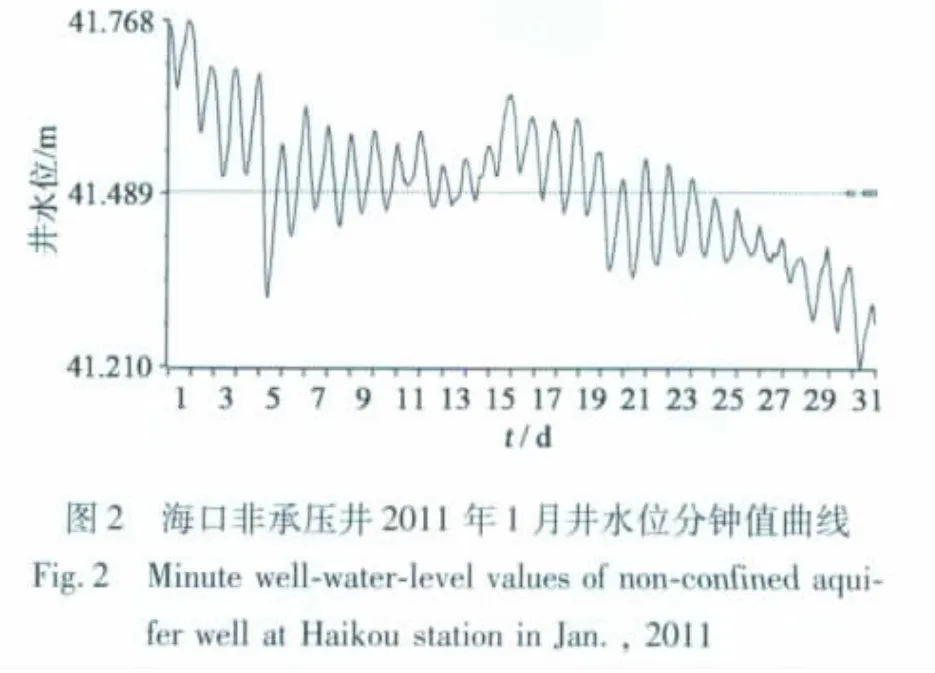
虽然图2 中该井为非承压井，但仍然像图1 所示的承压井一样，可记录到固体潮。因此，凡是能清晰记录到固体潮的承压井和非承压井皆为作为一种天然体应变计。不过，前者的放大倍数为，后者放大倍数为，前者的放大倍数可高达2.2 ×10－5～(0.44 ～1)×107m，为一个确定的常数。后者的放大倍数是随井孔半径而变的，且与有效水体积有关，因而是不确定的。

由于非承压井多少具有一定的承压性，因此承压井与非承压井水位皆可作为一个天然体应变观测系统，在正式使用之前都必须进行标定，以确定其观测格值。一个观测系统的观测格值为该系统的放大倍数之倒数。虽然承压井水位的理论放大倍数为，但由于我们无法事先知道该含水层的孔隙度，因此也就无法取得k 值。即使已知理论格值，但在观测前都必须进行标定。由于我们无法人工输入体应变，但考虑到井水位能记录到体应变固体潮，因此可用体应变固体潮理论值作为人工激励，把井水位观测值作为其响应，根据固体潮理论［9，12］，井水位观测值的整点值的维尼迪柯夫调和分析结果中的M2波的潮汐因子的倒数即为观测格值［2］，在取得了观测格值后，我们就可把以长度为量纲的井水位观测值转换成体应变观测值，使观测值具有明确的地球物理含义。

致谢感谢顾申宜同志提供相关数据!

1 王吉易，董守玉，陈建民.地下流体地震预报方法［M］.北京:地震出版社，1997.(Wang Jiyi，Dong Shouyu and Chen Jianmin.The methods of earthquake prediction based on subsurface fluid observation［M］.Beijing:Seismological Press，1997)

2 刘序俨，等.承压井水位观测系统对体应变的响应机制分析［J］.地球物理学报，2009，52(12):3 147－3 158.(Liu Xuyan，et al.Response analysis of the well-water-level system in confined aquifer［J］.Chinese Journal of Geophysics，2009，52(12):3 147－3 158)

3 M A Biot.General theory of three-dimensional consolidation［J］.Appl.Phys.1994，12:155－164.

4 J R Rice and M P Cleary.Some basic stress diffusion solution for fluid-saturated elastic poroces media with compressible constituents［J］.Rev Geophys spoce phys.，1976，14:227－241.

5 晏锐，等.从昌平体应变、水位对地震波的响应特例求算含水层的skempton 常数［J］.地震学报，2008，30(2):144－151.(Yan Rui，et al.Calculating B value of aquifer from volume strain and water level response to seismic waves at Changping seismic station［J］.Acta Seismologica Sinica ，2008，30(2):144－151)

6 Paul P U.College physics［M］.北京:机械工业出版社，2003.(Paul P U.College physics［M］.Beijing :Mechanical Industry Press，2003)

7 E·约翰芬纳莫尔，约瑟夫B·弗朗兹尼.钱翼稷，等译.流体力学及其工程应用［M］.北京:机械工业出版社，2006.(Finnemore E J and Franzini J B.Translates by Qian Yiji，et al.Hydrodynamics and its engineering applications［M］.Beijing:Mechanical Industry Press，2006)

8 毛根海，邵卫云，张燕.应用流体力学［M］.北京:高等教育出版社，2006.(Mao Genhai，Shao Weiyun and Zhang Yan.Application of fluid mechanics［M］.Beijing:Higher Education Press，2006)

9 P·梅尔基奥尔著.杜品仁，等译.行星地球的固体潮［M］.北京:科学出版社，1984.(Melchior P.Translated by Du Pinren，et al.The tides of the planet earth［M］.Beijing:Science Press，1984)

10 Farrell W E.Deformation of Earth by surface loads［J］.Reviews of Geophysics and Space Physics，1972，10(3):761－797.

11 李春洪，陈益惠，田竹君.井－含水层系统对固体潮的动态响应及其影响因素［J］.中国地震，1990，6(2):37－45.(Li Chunhong，Chen Yihui and Tian Zujun.The dynamic response of well aquifer system to earth tides and its influence factors［J］.Chinese Earthquake，1990，6(2):37－45.

12 北京大学地球物理系，武汉测绘学院大地测量系，中国科学技术大学地球物理教研室编.重力与固体潮［M］.北京:地震出版社，1982.(The Earth Physics Department of Peking University，the Geodetic Survey Department of Wuhan Survey Institute，the Geophysics Staff Room of University of Science and Technology of China.Gravity and Earth tide［J］.Beijing:Seismological Press，1982)

13 Chia Y P，et al.Changes of ground water level due to the 1999 Chi-Chi earthquake in the Choshui river Alluvial Fan［J］.Bulletin of Seismological Society of America ，2001，91(5):1 062－1 068.

14 张素欣，杨卫东，张子广.唐山矿井模拟与数字水位的记震能力对比分析［J］.西北地震学报，2007，29(2):170－173.(Zhang Suxin，Yang Weidong and Zhang Ziguang.Comparison of the ability of recording seismic wave between digital and analogue groundwater level observation in Tangshan mine well［J］.Northwestern seismological Journal，2007，29(2):170－173)