基于土层位移差的地下结构抗震反应位移法分析

董正方，王君杰，王文彪，姚毅超

(同济大学 桥梁工程系，上海 200092)

20世纪70年代，研究者据地下结构地震反应特征提出地下结构抗震设计的反应位移法。文献［1-6］对其地基弹簧刚度、地震荷载的确定开展大量研究。

反应位移法所需的土层沿深度变化地震位移、剪应力、加速度等数据可通过土层一维地震反应分析获得。工程场地地震安全性评价中会提供地震动位移随深度的变化，且地震动峰值位移沿深度取值方法已有研究成果，直接应用该成果可得土层沿深度变化的地震位移，但一般得不到土层剪应力。因此研究土层剪应力未知时，直接基于土层位移差求解反应位移法很有必要。

1 反应位移法理论推导

分析时分解成挖空土层与结构，如图1所示。其中FI为二者相互作用力向量;uI为二者接触面总位移向量，等于挖空土层的位移uII与相互作用力FI产生的位移uI2之和;FI=kuI2，k为地基弹簧刚度矩阵。忽略阻尼影响，结构运动方程为:

式中:下标I表示结构与土层接触面节点，S表示其余节点;M，K为质量、刚度矩阵;为加速度向量;R为影响系数向量;为地震加速度。

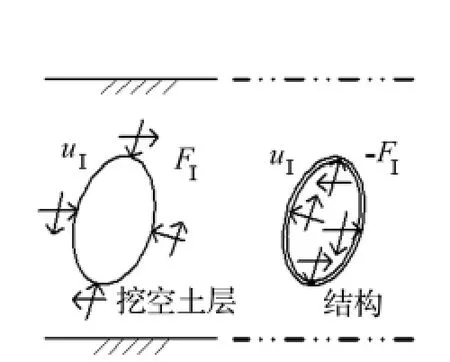
图1 体系分解示意图Fig.1 System decomposition

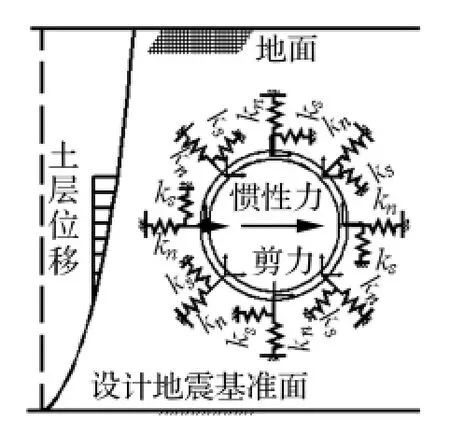
图2 反应位移法计算示意图Fig.2 Response displacement method

将FⅠ用刚度与位移替换，移项惯性力，得:

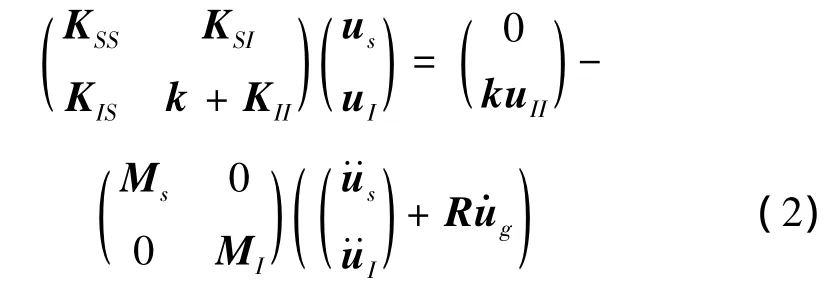
式中:右边加速度项括号内之和为绝对加速度;利用上式求解即可无需土层剪应力;uII为挖空土层位移，实际计算常用未挖空时位移uII，二者不同原因为存在土层之间的剪力FF;因此式(2)可改为:

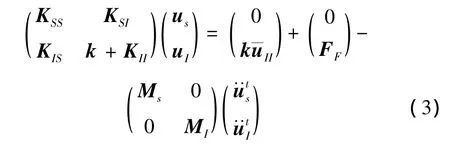
式中:上标t表示绝对加速度，式(3)即常用反应位移法理论方程。

推导过程表明，反应位移法的地震荷载包括土层相对位移差、土层剪应力、结构惯性力。文献［4］指出，除像输水隧道等内部质量很大以外，在一般隧道中，惯性力影响增加不足1%。因本文重点研究土层位移与剪应力影响，故可忽略惯性力。土层相对位移与剪应力一般通过土层一维地震反应分析得到;对土层简单情况，也可由计算得到［7］:

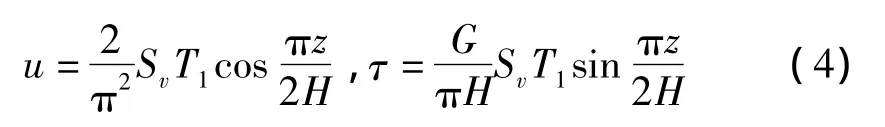
式中:u为土层位移，H为土层厚度，G为土动剪切模量，τ为土层剪应力，Sv为基岩速度反应谱，T1为土层特征周期，z为深度。用公式看似简单，实际却存在困难，尤其基岩速度反应谱国内并不常用。工程场地地震安全性评价中地震动位移随深度的变化及其它地震动峰值位移沿深度的取值方法，均为未挖空土层位移。使用反应位移法时，还需土层剪应力。但土层剪应力随深度变化的研究较少。由上述推导可知，若有挖空土层位移，反应位移法无需土层剪应力。

挖空土层位移可通过二维土层地震反应分析得到，但计算量较大;也可通过未挖空时位移得到挖空位移，只要知道二者关系即可。

2 土层位移关系

2.1 未挖空土层位移

无限土层在垂直向上的剪切地震波作用下的计算，可等效为在无限远处承受一定荷载Q的弹性理论平面接触问题，见图 3［8］。

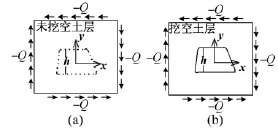
图3 平面接触模型Fig.3 Plane contact problem model

对图3(a)，由弹性理论知在h范围内的挖空土层的水平位移差为［9］:

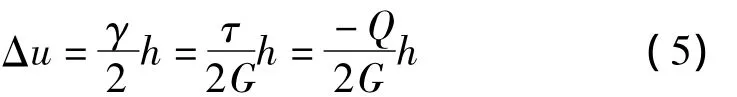
式中:γ为土层剪应变;Δu为h范围内土层位移差。

而对图3(b)需应用平面问题的复变函数理论求解出复势函数。将z平面上一个给定区域变成另一个复平面ζ上单位圆的外域映射函数普遍形式，用Laurent级数形式［10］表示为:

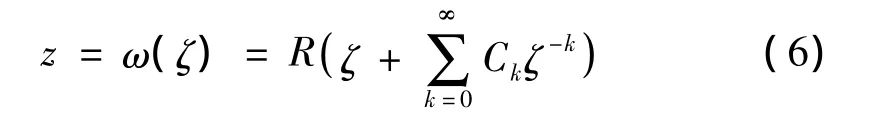
式中:R为正实数，反应孔形大小;工程结构通常至少有一个竖向对称轴，则Ck必为实数;一般情况下，级数中只需取很少几项即足够精确。

2.2 圆形孔挖空位移

对圆形孔，其映射函数变为［10］:

式中:R为圆孔半径。

其复势函数可表示为:

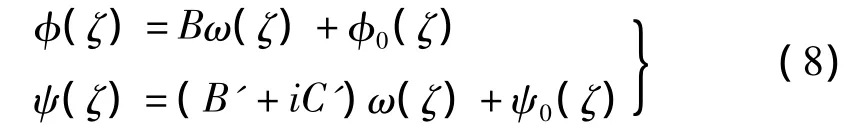
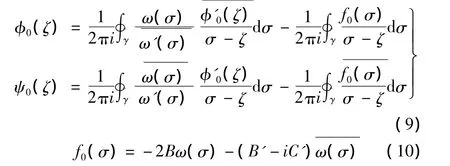
代入已知量，利用柯西积分公式，得:

由位移公式［9］:

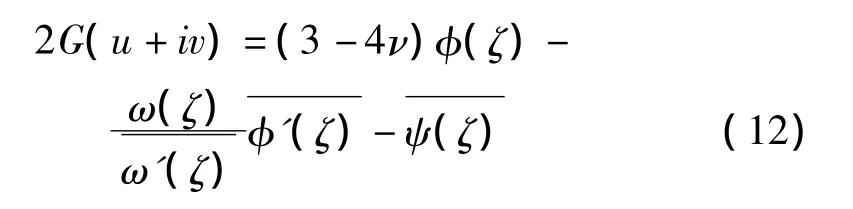
式中:ν为土体泊松比，分离实部与虚部得水平位移:

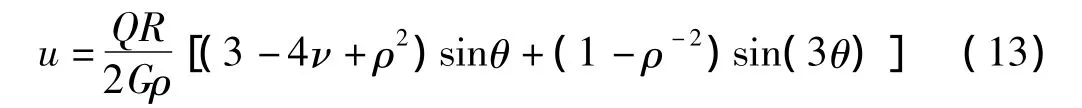
ρ取1，θ取 90°、270°时，可得圆孔上下部水平位移，二者相减得水平位移差为:

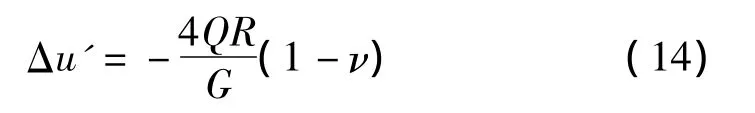
将式(5)代入，得两位移关系为:

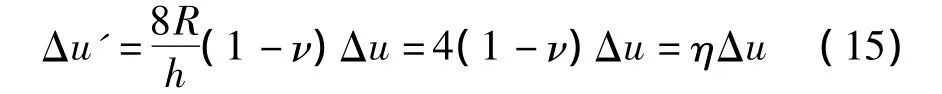
其中:η为位移差放大系数。因土体泊松比一般为0.2～0.4，故η的取值范围为2.4 ～3.2。

2.3 矩形孔挖空位移

对矩形孔，其映射函数变为［11］:

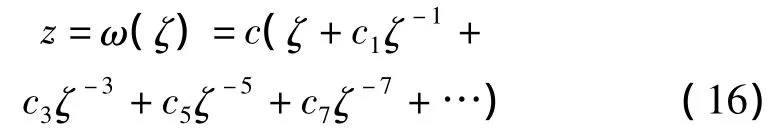
式中:c为与矩形大小有关的实数;cn(n=1，3，5，7)算式为［11］:

式中:k取决于矩形高宽比。c的计算式为:

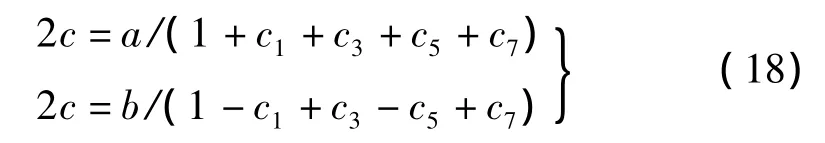
式中:a，b为矩形宽、高度。假设一个k，通过式(17)求出cn，可得计算高宽比λ:

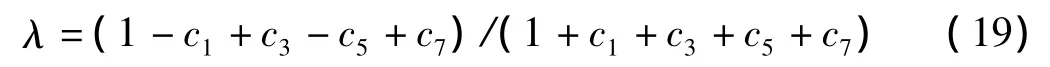
与实际高宽比b/a相比，反复迭代使误差满足要求，即可得到c。

为简化，映射函数可只取前两项。推导过程同圆形孔，篇幅所限，只给出最后结果:

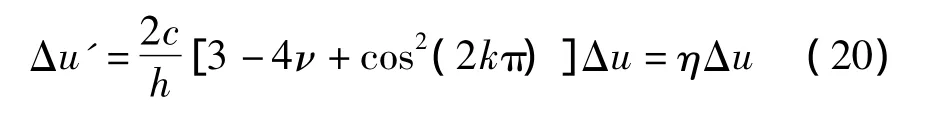
放大系数与土体泊松比及矩形形状有关。

3 算例

利用上述关系，用反应位移法即可由未挖空位移差得到挖空位移差，然后加到模型上，不再施加剪应力，可简化计算过程，尤其在未知剪应力时。用典型算例验证上述方法的适用性。

3.1 典型结构

选软土中典型盾构隧道及地下车站。盾构隧道外径7 m、内径6.3 m，中心埋深18.2 m;矩形地下车站高13 m、宽20.6 m，中心埋深9.467 m。土层参数按土层厚度加权平均，等效为中软土，土层厚度100 m下为基岩。其余参数见表1。结构尺寸见图4。

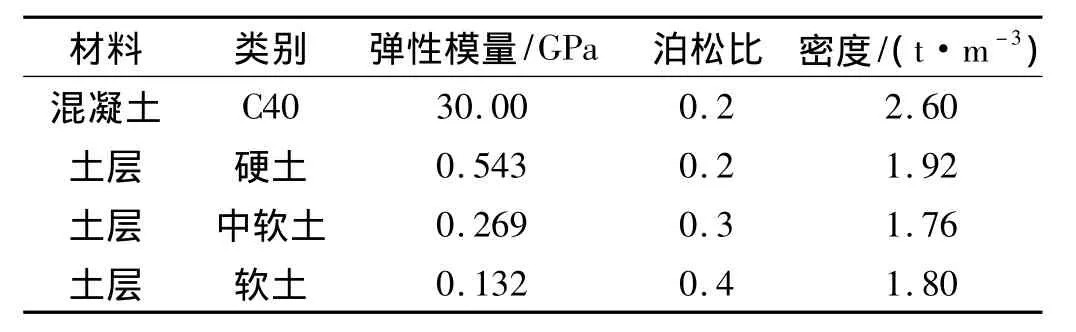
表1 材料参数Tab.1 Material parameters

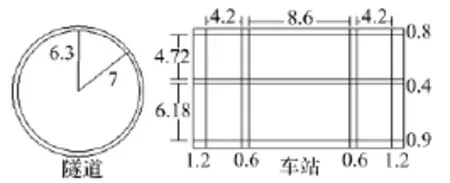
图4 结构尺寸图(单位:m)Fig.4 Cross section of structure(unit:m)

3.2 计算工况

考虑土体软硬程度的影响，分别用假设的硬土与软土代替中软土;考虑本文方法的适用性，反应位移法荷载分三种情况:① 使用一维土层地震反应分析计算位移差及剪应力，并作为基准工况;② 使用①的位移差，不加剪应力;③ 使用①的位移差乘以放大系数，不加剪应力。各计算工况见表2。

表2 计算工况Tab.2 Computational cases

以结构内力为对象，考虑水平地震作用，选计算模型中关键截面作为控制截面，如图5所示。

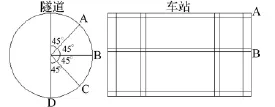
图5 结构截面力考察位置分布Fig.5 Distribution of observation points in the cross section

采用自编的Aduts有限元软件，用三种方法分别计算不同工况。一维自由土层地震反应计算用Pro-Shake，土应力-应变特性曲线与阻尼特性曲线分别用Seed和Idriss提出的砂土模型曲线;为较全面验证，基岩输入地震波采用Taft波(下称Ta波)、Treas波(下称Tr波)及Petrolia波(下称Pe波)，如图6所示，峰值加速度调整为0.1 g。

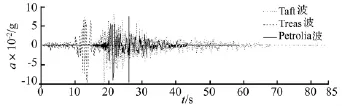
图6 三条地震波Fig.6 Three earthquake accelerograms

3.3 基本参数计算结果

反应位移法地基弹簧刚度用静力有限元法计算;盾构隧道压缩弹簧刚度取平均值，剪切弹簧刚度取压缩刚度的0.5倍［12］;地下车站底板、顶板、侧板地基压缩弹簧刚度分别取平均值，剪切弹簧刚度分别取压缩弹簧刚度的1/3［13］。土层动剪切模量取一维自由土层地震反应结果;位移差放大系数按式(15)、(20)计算。Ta波结果见表3。

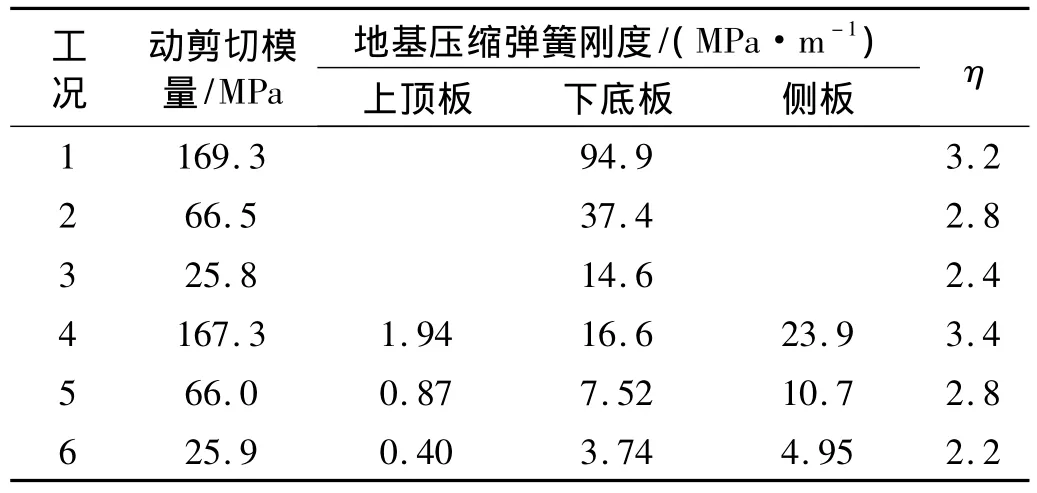
表3 基本参数Tab.3 Essential parameters

3.4 结构内力计算结果

结构位置处的内力最大值见表4、表5，误差是相对法1的，车站A点取侧板顶部内力，车站B点取侧板弯矩及剪力、中板轴力。篇幅所限，只给出工况2、5的Ta波弯矩、剪力、轴力的分布图，如图7～图12，其它工况结果类似。

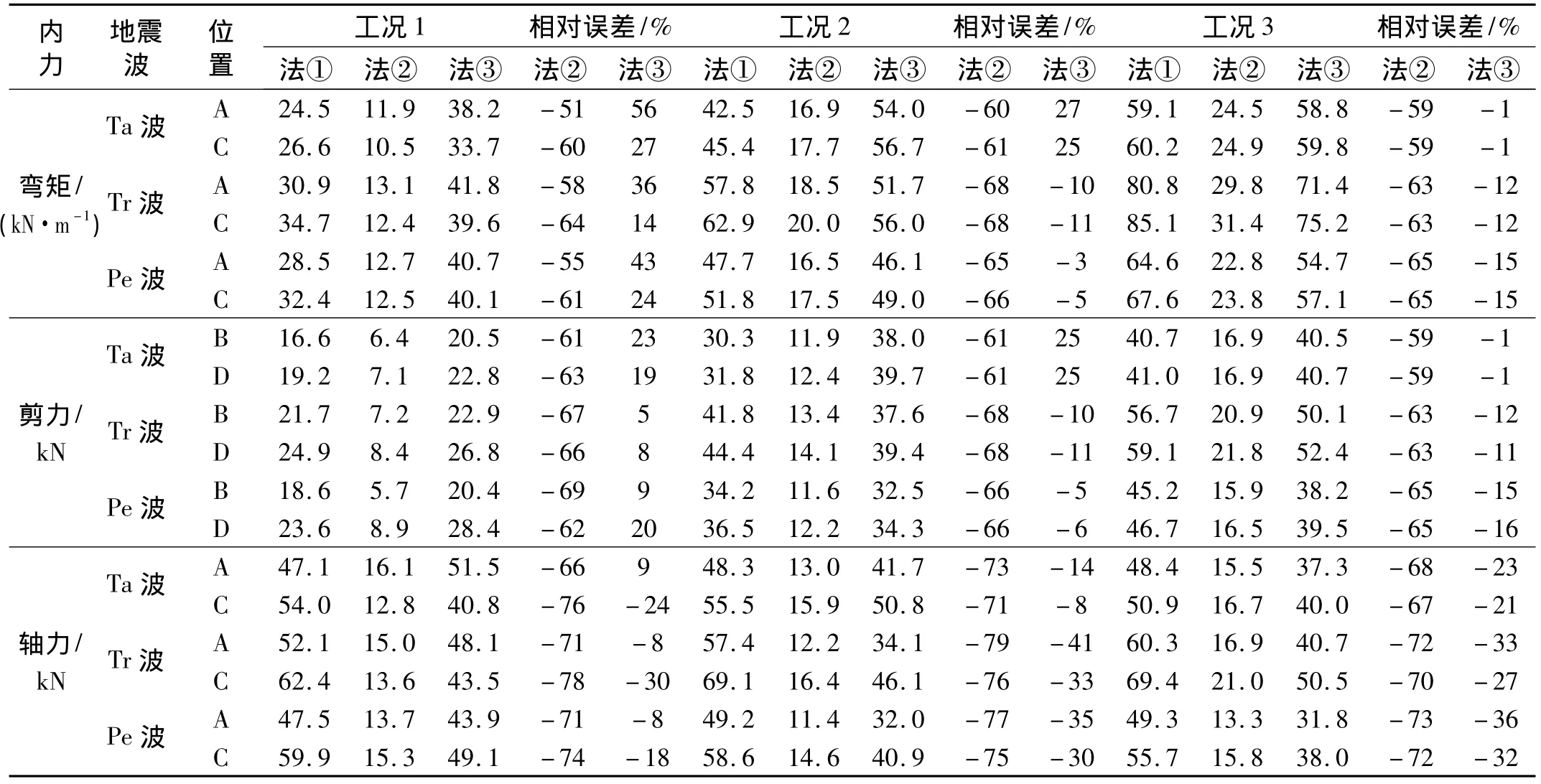
表4 隧道截面内力Tab.4 Results of force in cross section of the tunnel

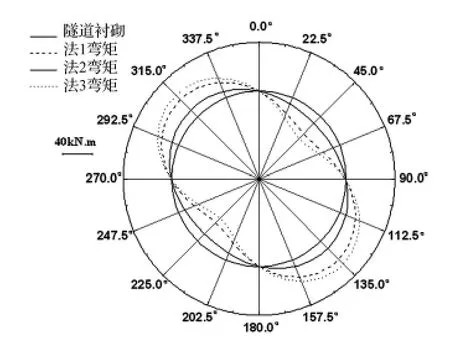
图7 隧道弯矩分布图Fig.7 Moment distribution of the tunnel

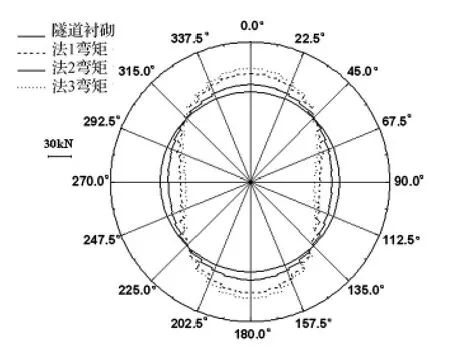
图8 隧道剪力分布图Fig.8 Shear force distribution of the tunnel

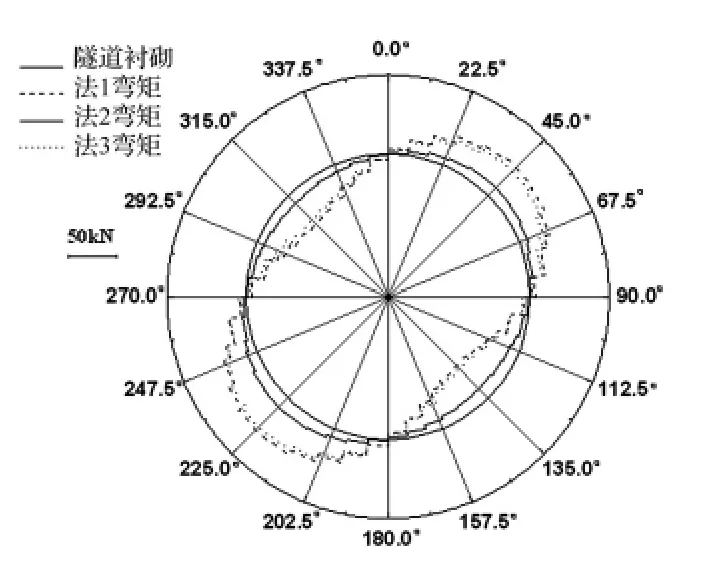
图9 隧道轴力分布图Fig.9 Axial force distribution of the tunnel

表5 车站考察截面的内力Tab.5 Results of force in cross section of the station

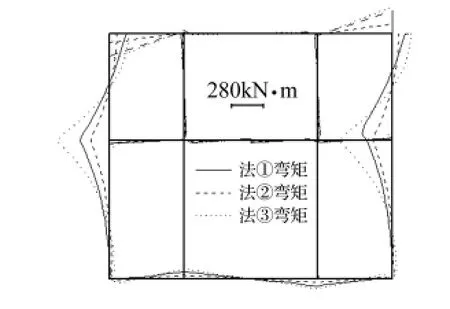
图10 车站弯矩分布图Fig.10 Moment distribution of the station

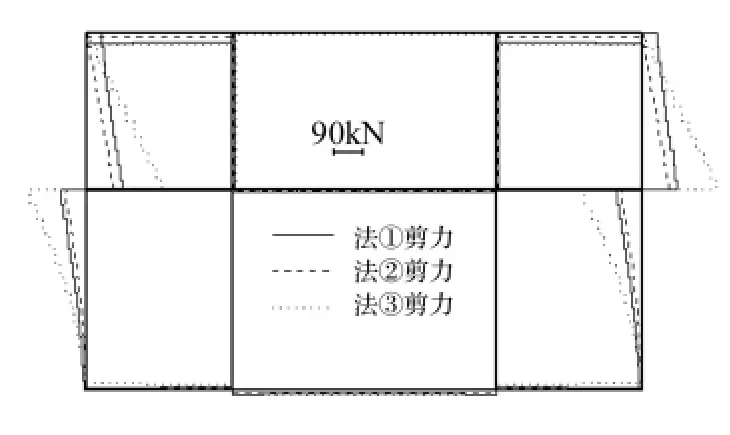
图11 车站剪力分布图Fig.11 Shear force distribution of the station

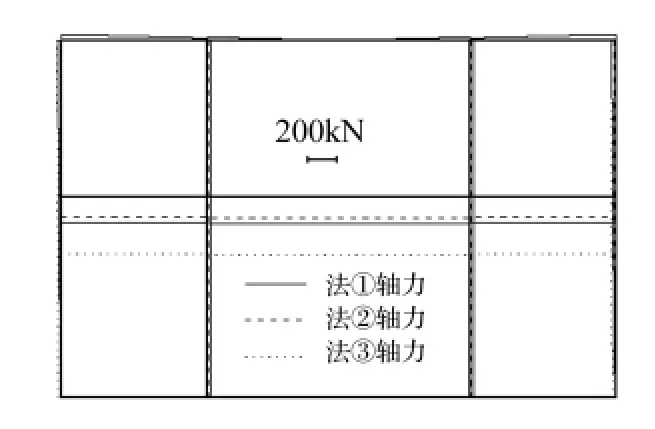
图12 车站轴力分布图Fig.12 Axial force distribution of the station

由内力结果看出:尽管三条地震波的频谱特性不同，但其内力随土层软硬变化的规律基本一致;三种方法的内力分布形式基本一致;关键截面处内力随土层由硬变软，误差由大变小，说明不太适宜硬土情况。

对圆形隧道，不考虑土层剪应力时，关键截面内力结果偏小60%左右，最大达约80%，与文献［14］结论基本一致，土层剪应力影响较大，不能忽略。用挖空位移时，关键截面弯矩及剪力硬土情况下偏大、软土情况下偏小;截面剪力和弯矩偏大对截面验算偏于安全，偏小误差在11%以内;截面轴力偏小，但较不考虑剪力时误差更小，偏小原因为地基弹簧刚度求解时忽略弹簧之间的相互影响也会造成轴力偏小［4］，通过提高地基弹簧刚度精度，误差会减小;放大系数基于深埋，埋深增加，误差也会减小;因此本文方法可行。

对矩形车站，不考虑土层剪应力时规律与圆形隧道一致，故土层剪应力影响也不能忽略。用挖空位移时，关键截面内力一般偏大，个别情况偏小，偏小误差在10%以内;虽截面内力有情况下偏大达约1.7倍，但较偏小安全。矩形车站误差较大的重要原因为地基弹簧刚度求解存在误差，而土层位移差作用在结构上通过地基弹簧，因此弹簧刚度误差传递到内力上;另一个原因是位移放大系数求解时，只取映射函数的前两项，也会造成误差;另外车站埋深较浅，而本文放大系数基于深埋;通过提高弹簧刚度精度、映射函数多取几项、针对深埋结构，可减少误差，因此本文方法也是可行的。

4 结论

本文对基于土层位移差的反应位移法求解进行研究，并通过典型圆形隧道与矩形车站算例验证，结论如下:

(1)本文给出的无限均匀介质中未挖空位移与挖空位移的解析关系，适用于土层均匀单一的圆形和矩形孔;土层位移差的放大系数，对圆形孔仅与土层泊松比有关，对矩形孔则与矩形形状有关。

(2)基于土层位移差的反应位移法适用于土层剪应力难以获取场合及埋深较大的地下结构;不适用硬土土情况。

(3)该法精度依赖于地基弹簧刚度的求解精度，对地基弹簧刚度求解要求较高。

本文提出的方法拓宽了反应位移法的使用范围，适用于地下结构前期设计的抗震分析。

［1］川岛一彦.地下構造物の耐震設計［M］.日本:鹿島出版株式會社，1994.

［2］Nishida M，Matsui T.Applicability of seismic deformation method to aseismic analysis of underground linear structure［C］.14thInternational Offshore and Polar Engineering Conference，2004:600-606.

［3］Kawashima K.Seismic analysis of underground structures［J］.Journal of Disaster Research，2006，1(3):378-389.

［4］小泉淳著.张稳军，袁大军译.盾构隧道的抗震研究及算例［M］.北京:中国建筑工业出版社，2009.

［5］黄茂松，曹 杰.隧道地震响应简化分析与动力离心试验验证［J］.岩石力学与工程学报，2010，29(2):271-280.

HUANG Mao-song，CAO jie.Simplied analysis of tunnel earthquake response and centrifuge modeling calibration［J］.Chinese Journal of Rock Mechanics And Engineering，2010，29(2):271-280.

［6］刘晶波，王文晖，赵冬冬.地下结构地震反应计算反应位移法的改进［J］.土木建筑与环境工程，2010，32(S2):211-213.

LIU Jing-bo，WANG Wen-hui，ZHAO Dong-dong.Improvement ofresponse displacementmethod ofseismic analysis of underground structures［J］.Journal of Civil，Architectural＆Environmental Engineering，2010，32(S2):211-213.

［7］建設省土木研究所地震防災部耐震研究室.大規模地下構造物の耐震設計法·ガィドラィン(案)［R］.日本:土木研究所資料，1992.

［8］福季耶娃著.徐显毅译.地震区地下结构物支护的计算［M］.北京:煤炭工业出版社，1986.

［9］ England A H.Complex variable methods in elasticity［M］.New York:Dover Publications，2003:24-25.

［10］吕爱钟，张路青.地下隧洞力学分析的复变函数方法［M］.北京:科学出版社，2007.

［11］赵 凯，刘长武，张国良.用弹性力学的复变函数法求解矩形硐室周边应力［J］.采矿与安全工程学报，2007，24(3):361-365.

ZHAO kai，LIU Chang-wu，ZHANG Guo-liang.Solution for perimeter stresses of rocks around a rectangular chamber using the complex function of elastic mechanics［J］.Journal of Mining＆ Safety Engineering，2007，24(3):361-365.

［12］谷 音，刘晶波，杜义欣.三维一致粘弹性人工边界及等效粘弹性边界单元［J］.工程力学，2007，24(12):31-37.

GU Yin，LIU Jing-bo，DU Yi-xin.3D consistent viscousspring artificial boundary and viscous-spring boundary element［J］.Engineering Mechanics，2007，24(12):31-37.

［13］鉄道総合技術研究所.鉄道構造物等設計標準·同解說:耐震設計［S］.東京:丸善株式会社，2000.

［14］水野 光一朗，小泉 淳.シールドトンネル横断方向の耐震設計法に関する基礎的研究［C］.日本土木学会論文集，2001(687):107-123.