Timoshenko梁功率流主动控制研究

王有懿，马文来，赵 阳

(哈尔滨工业大学 航天学院，哈尔滨 150001)

梁式结构应用广泛，如航天器天线杆、相机支架、太阳能帆板轴等。飞轮及陀螺等高速旋转部件的中、高频扰动在航天器梁式结构中传播，会引起结构抖动。由于环境阻尼较小，此抖动将长时间持续存在，影响天线、相机等高精度敏感设备的正常工作，降低精度。因此，对梁式结构进行抖动分析与控制研究具有重要的理论价值与工程实际意义。

扰动引起结构动态响应的主要研究方法有:有限元方法、统计能量法、行波方法等。在分析结构中、高频动态特性时，有限元方法与统计能量法均表现出各自的不足;而行波方法计算结构动力学响应一般无频率限制，具有鲁棒性［1］。在行波方法基础上引入“功率流”方法，该方法综合力与速度响应大小及相位关系，能给出结构内的局部能量分布及功率流传播路径，可揭示整个系统的能量分布，为研究复杂系统振动的有效工具。功率流主动控制方法克服了传统模态控制方法与数学模型紧密相关及控制频率受限的缺点和不足，主要功能为隔离结构中能量的传递，仅通过最小化功率流即可减小结构整体抖动。功率流模型可描述结构中振动传播，为振动控制设计中重要的控制优化特征量。Miller等［1］首先采用行波方法处理结构振动问题;Mace等［2-4］采用单一传感器与单一作动器研究梁弯曲波的同位反馈控制与自适应前馈控制以及近场影响下梁弯曲波的主动控制;Schwenk等［5］提出用于控制梁结构振动功率流的算法。Audrain等［6］研究了梁结构功率流控制理论，并进行实验验证。Pereira等［7］采用基于最小化结构功率流实部的控制方法，降低了梁结构整体抖动;刘春川等［8-9］采用波动方法研究了有限L型梁结构功率流主动控制;朱宏平等［10］采用导纳波动方法研究了建筑结构功率流主动控制策略。宋孔杰等［11］对柔性隔振系统功率流理论进行了深入研究。金全洲等［12］研究了圆柱壳结构功率流主动控制方法。以上研究对梁结构动力学分析与控制主要采用Euler-Bernoulli经典梁理论，用Timoshenko梁理论则较少。经典梁理论在结构动力学分析中具有局限性，Timoshenko梁理论因考虑横向剪切变形与转动惯量影响，更适用于结构的中、高频振动研究，其分析结果更接近工程实际。Carvalho等［13］基于波动吸收方法研究了无限长Timoshenko梁中弯曲波的主动控制;Mei等［14-15］对Timoshenko梁结构的波反射、透射及振动主动控制的混合波/模方法进行研究，其波动控制策略采用同位配置反馈控制。总之，尽管基于Euler-Bernoulli梁理论的结构功率流研究已相对成熟，但关于Timoshenko梁结构功率流研究甚少。

本文基于Timoshenko梁理论，考虑梁中转动惯量及剪切效应，建立悬臂梁结构的行波动力学模型，分析扰动对梁结构动态特性影响。通过理论仿真与分析，研究Timoshenko梁结构中的功率流传播及主动控制方法，为梁耦合结构、桁架结构的抖动分析与控制研究提供基础。

1 悬臂Timoshenko梁行波动力学模型

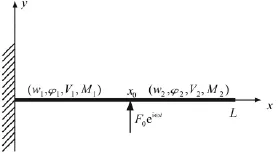
图1 悬臂Timoshenko梁模型Fig.1 The cantilever Timoshenko beam model

图1为悬臂Timoshenko梁结构，由于该梁包含剪切变形与转动惯量影响，其波动动力学方程为:

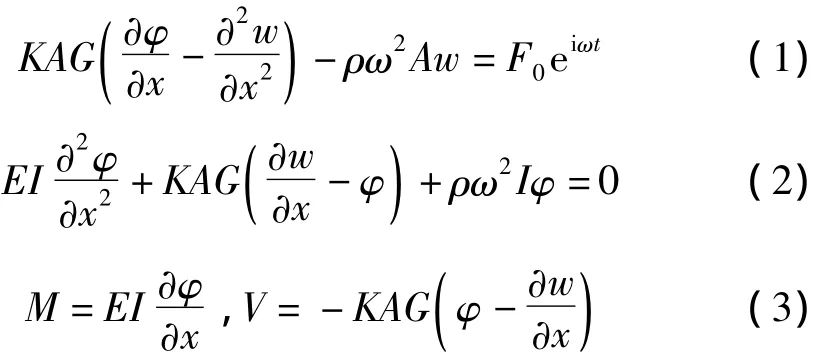
式中:w，φ分别为弯曲波位移、转角;M，V为弯矩、剪力;E为弹性模量;I为梁惯性矩，I=Ah2/12，A为梁横截面面积;h为横截面高度;ρ为梁密度，K为剪切折算系数，K=π2/12。

根据行波理论，Timoshenko梁弯曲波位移与转角的行波解为:

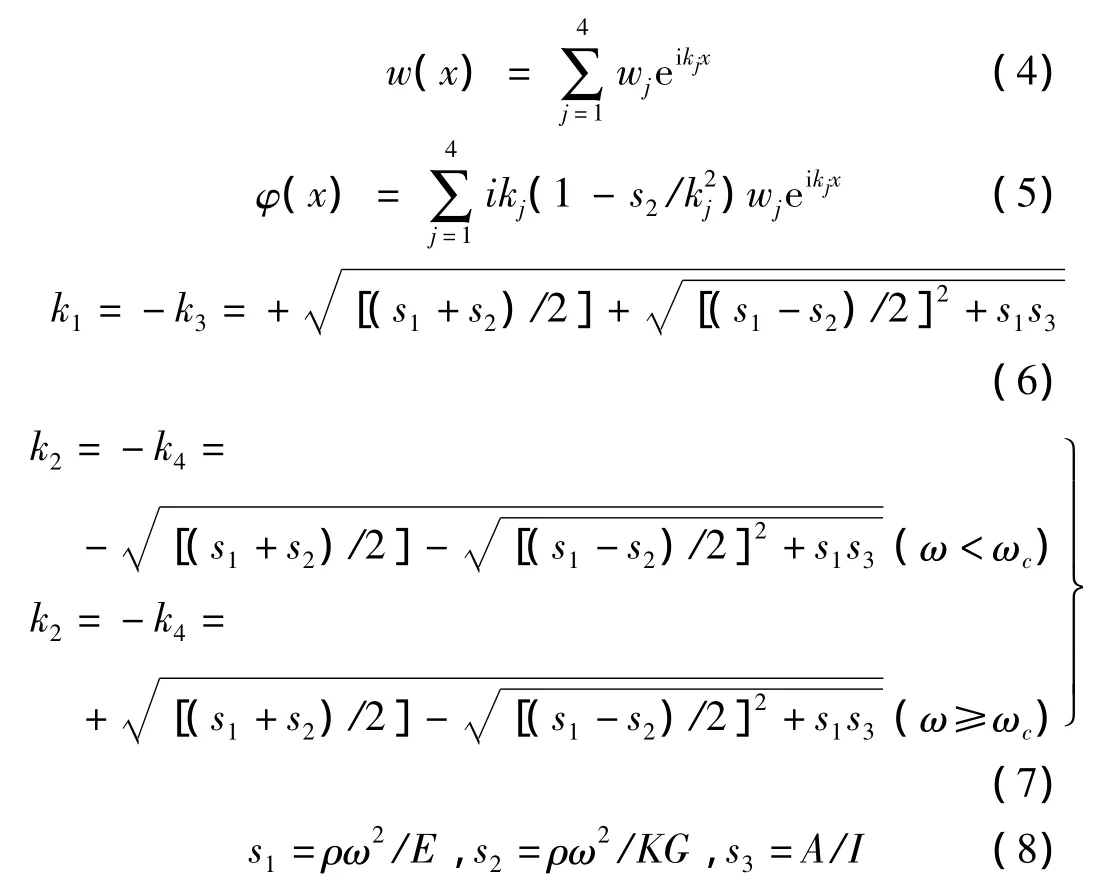
图1悬臂梁结构，力F0eiωt作用的左右弯曲波位移、转角、剪力、弯矩分别为w1，φ1，V1，M1与w2，φ2，V2，M2。考虑力作用不连续处x=x0的力平衡条件及位移连续条件得:

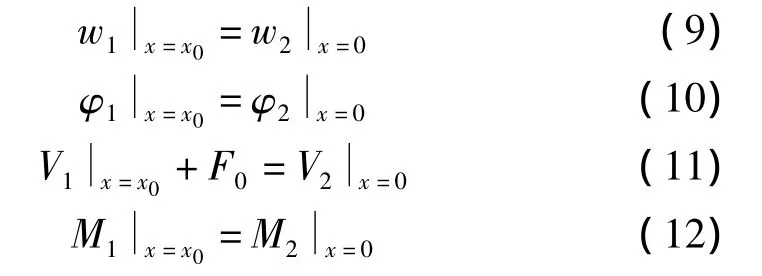
由梁两端边界条件得:

在x=0处:

在x=L处:

由此，考虑边界条件、力作用点处连续条件得方程组为:

式中:［α］为8×8维系数矩阵，由边界条件、力作用处连续条件确定;{A}={A1，A2，A3，A4，A5，A6，A7，A8}T为波谱系数矩阵;{F}={0，0，0，F0，0，0，0，0}T为激励源矩阵。

由上可知，只要给出具体参数值，便可求出式(17)中的{A}，代入式(1)、式(2)可得悬臂梁结构任意位置的动力响应。

作用于x0位置的扰动力F0eiωt在悬臂梁任意位置响应可表示为:

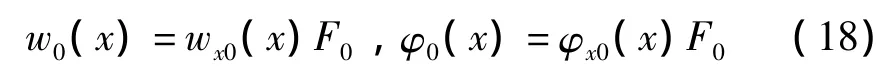
式中:wx0(x)、φx0(x)为单位力产生的弯曲波位移及转角。

2 Timoshenko梁功率流传播分析与主动控制

功率流为结构中某一截面能量传递的时间平均。在Timoshenko梁结构中某x位置截面处的主动功率流可表示为［8］:

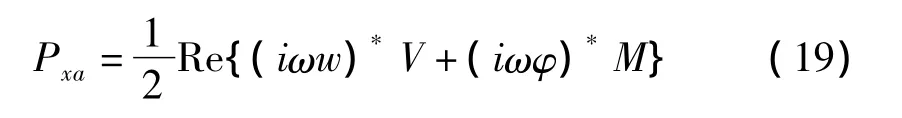
式中:w，φ为弯曲波位移和转角;V，M为剪力、弯矩，*为共轭转置符号，Re表示取实部。

前馈主动控制算法广泛应用于梁、板及组合结构中。因此，在Timoshenko梁结构行波动力学建模基础上，对梁结构进行功率流主动控制，以抑制梁式结构振动功率流的传递。

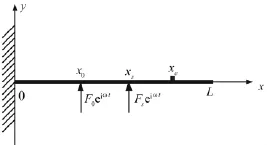
图2 Timoshenko梁功率流主动控制图Fig.2 The diagram of power flow active control for Timoshenko beam

由图2，扰动力作用于x0位置，控制力作用于xs位置，由式(18)，控制力Fseiωt产生的响应为:

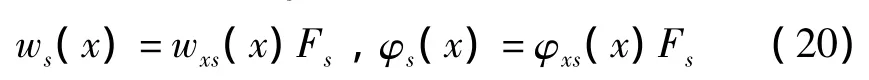
式中:wxs(x)、φxs(x)同wx0(x)、φx0(x)，仅主动控制力Fseiωt作用位置处连续条件不同。

由式(18)、式(20)知，当扰动力与控制力共同作用时，悬臂梁的弯曲波位移、转角为:

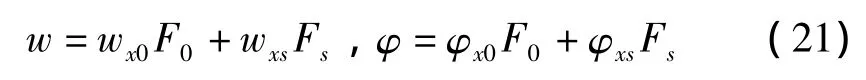
弯矩、剪力为:

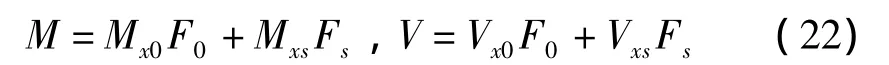
将式(21)、(22)代入式(19)得:

式中:

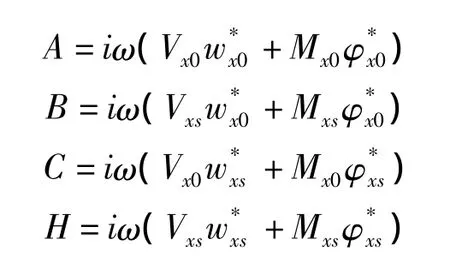
由功率流Pxa对控制力Fs的实部与虚部偏导数为0，得最优控制力为:

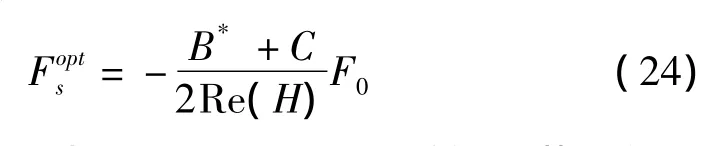
将式(24)代入式(23)可得通过悬臂梁x截面的最小功率流。即通过优化功率流获得控制力大小、相位，以实现梁式结构功率流传播的主动控制。

3 仿真算例与分析

以悬臂Timoshenko梁为例进行数值计算分析，首先计算其动力学响应并与有限元方法计算结果比较，分析行波方法计算结构动态特性的精确性;在此基础上，基于Timoshenko梁理论获得结构中传播的功率流，并与Euler-Bernoulli经典梁结果对比;通过计算分析，对梁结构进行功率流主动控制，对比Timoshenko梁控制前后传播的功率流，验证功率流主动控制方法的正确性与有效性。

3.1 动力学响应仿真算例与分析

图2悬臂Timoshenko梁结构几何尺寸:长L=4 m，宽度b=0.02 m，厚度h=0.02 m;弹性模量E=2.0 ×1011N/m2;密度ρ=7 800 kg/m3;泊松比ν=0.3;阻尼因子η=0.001;扰动力F0eiωt(F0=1 N)作用于x0=1 m 处;控制力Fseiωt作用于xs=2.5 m 处;误差传感器位于xe=3 m处。仿真结果见图3、图4。

图3为扰动力F0eiωt作用于悬臂梁x0=1 m处时，x=3 m处横向位移频响函数的行波解及将结构分别划分为64、128、256梁单元的有限元解。

图4为分别基于Timoshenko梁理论与Euler-Bernoulli经典梁理论x=3 m截面处功率流对比。

图3 有限元与行波方法计算Timoshenko梁动力学响应Fig.3 Comparison of dynamic response in the Timoshenko beam by FEM and traveling wave method

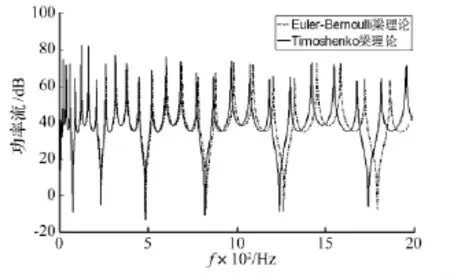
图4 Timoshenko梁理论与Euler-Bernoulli梁理论计算悬臂梁结构中功率流Fig.4 Power flow of cantilever beam calculated by Timoshenko and Euler-Bernoulli beam theory

由图3看出，基于模态叠加的有限元方法计算结果在低频段与行波方法计算结果吻合较好。在中、高频段，随着单元的增加，有限元方法解逐渐趋向行波解。其差别原因在于有限元采用模态叠加方法，在求解过程中存在截断误差，且高阶模态计算不准确;而行波方法不受模态限制，可精确计算结构在全频域的响应。

由图4知，两种梁理论计算功率流的结果不同，由Timoshenko梁理论计算的共振频率明显低于由Euler-Bernoulli梁理论计算结果。其原因为:Euler-Bernoulli梁理论中未考虑结构剪切变形影响，梁的剪切刚度认为无穷大，而梁的实际剪切刚度是有限的。Timoshenko梁理论中考虑了剪切变形及转动惯量影响，在高频段及中、低频段影响梁结构的功率流传播，使计算的共振频率低于Euler-Bernoulli理论结果，且结果更接近真实梁结构的动态特性。

3.2 功率流主动控制仿真算例

对图2悬臂Timoshenko梁进行功率流主动控制仿真，初始条件同3.1节。图5～图7分别为主动控制前后功率流对比图、最优控制力图及控制力作用不同位置的功率流主动控制效果图。

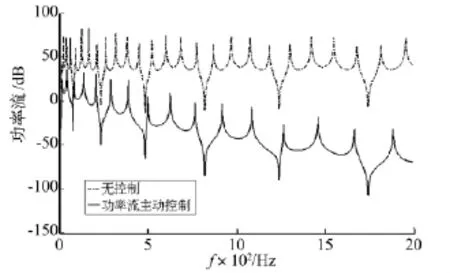
图5 x=3 m截面处控制前后功率流对比(dB ref:10-10w)Fig.5 Comparison of power flow atx=3 m with control and without control(dB ref:10-10w)

图5、图6分别为悬臂Timoshenko梁功率流主动控制效果图及最优控制力图。由图5看出:用功率流主动控制方法可明显降低梁结构中功率流传播，且在全频域中功率流平均衰减约60 dB。因此，功率流主动控制可实现结构在全频域范围的最优控制。由最优功率流优化可得图6的控制力，通过前馈、x滤波、最小均方(LMS)、自适应算法可抑制结构振动功率流传递。

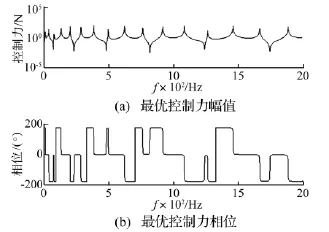
图6 功率流主动控制下的最优控制力Fig.6 The optimal control force with active control of power flow

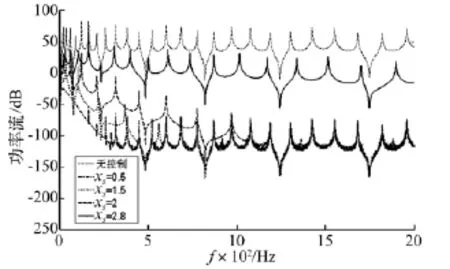
图7 控制力作用于不同位置处的功率流Fig.7 The power flow for different locations excited by control force

图7为控制力作用于悬臂Timoshenko梁不同位置的功率流控制效果图。由图7看出:① 无论控制力作用于悬臂梁结构的任何位置，只要通过优化功率流给出控制力并施加控制均可较好实现悬臂梁结构全频率下功率流主动控制［16］，且控制力位置距误差传感器越远，控制效果越明显。其原因在于:当控制力作用位置接近误差传感器位置，控制力近场效应会对误差传感器产生影响，进而影响控制效果。② 低频段控制力位置对控制效果影响显著，但对中高频段，控制力位置对功率流的控制效果影响较小。其原因为近场效应影响随频率的升高而逐渐减少［4］。

4 结论

本文对Timoshenko梁结构功率流主动控制方法进行理论研究，基于行波方法，建立Timoshenko梁结构动力学方程并计算其动力学响应，在仿真分析并与Euler-Bernoulli梁理论进行对比基础上，研究Timoshenko梁结构的功率流主动控制方法，结论如下:

(1)行波方法可精确计算Timoshenko梁结构全频域动力学响应;

(2)通过Timoshenko梁理论与Euler-Bernoulli经典梁理论计算结果对比，因Timoshenko梁理论考虑剪切变形及转动惯量影响，共振频率明显低于Euler-Bernoulli经典梁理论计算结果;而在中高频动力学响应分析中，Timoshenko梁理论结果更精确，且分析结果更接近工程实际。

(3)在Timoshenko梁行波动力学模型基础上，可获得Timoshenko梁结构中传播的功率流，以此为目标函数，经优化控制力可实现结构整体抖动控制。

(4)功率流主动控制能克服传统方法中高频控制受限与不能有效控制中高频扰动的缺点及不足，实现梁结构全频域的抖动抑制，且控制力位置选择对功率流主动控制效果影响甚微。

本文基于Timoshenko梁理论给出的悬臂梁精确动力学模型与功率流主动控制方法，可应用于耦合梁、平面与空间桁架等更复杂的梁式结构中。

［1］Miller D W，Von Flotow A H.A travelling wave approach to power flow in structural networks［J］.Journal of Sound and Vibration，1989，128(1):145-162.

［2］Mace B R，Jones R W.Feedback control of flexural waves in beams［J］.Journal of Structural Control，1996，3(1-2):89-98.

［3］ Halkyard C R，Mace B R.Feedforward adaptive control of flexural vibration in a beam using wave amplitudes［J］.Journal of Sound and Vibration，2002，254(1):117-141.

［4］Halkyard C R，Mace B R.Adaptive active control of flexural waves in a beam in the presence of a nearfield［J］.Journal of Sound and Vibration，2009，285(1-2):149-171.

［5］Schwenk A E，Sommerfeldt S D，Haye S I.Adaptive control of structural intensity associated with bending waves in a beam［J］.The Journal of the Acoustical Society of America，1994，96(5):2826-2835.

［6］Audrain P，Masson P，Berry A.Investigation of active structural intensity control in finite beams:theoryand experiment［J］.The Journal of the Acoustical Society of America，2000，108(2):612-623.

［7］Pereira A K A，Moreiraf F J O，Arruda J R F.Active control of the structural intensity in beams using a frequency domain adaptive method［J］.AIAA，1989，798:841-849.

［8］Liu C C，Li F M，Huang W H.Active vibration control of finite l-shaped beam with travelling wave approach［J］.Acta Mechanica Solida Sinica，2010，23(5):377-385.

［9］刘春川.基于波动理论的有限尺寸结构短时瞬态响应与功率流控制［D］.黑龙江:哈尔滨工业大学，2009.

［10］朱宏平，徐荣光.基于功率流的结构主动控制方法［J］.振动与噪声控制，1998(5):21-28.

ZHU Hong-ping，XU Rong-guang.Based on the power flow in active structural control method［J］.Journal of Vibration and Noise Control，1998(5):21-28.

［11］宋孔杰，张蔚波，牛军川.功率流理论在柔性振动控制技术中的应用与发展［J］.机械工程学报，2003，39(9):23-28.

SONG Kong-jie， ZHANG Wei-bo， NIU Jun-chuan.Application and development of power flow theories in the field of the vibration control for flexible systems［J］.Journal of Mechanical Engineering，2003，39(9):23-28.

［12］金全洲，李天匀，赵 耀，等.圆柱壳结构振动功率流和主动力幅值的控制研究［J］.船舶力学，2009，13(2):305-312.

JIN Quan-zhou，LI Tian-yun，ZHAO Yao，et al.Active control of cylindrical shells based on structure power flow and control inputs［J］.Journal of Ship Mechanics，2009，13(2):305-312.

［13］Carvalho M O M，Zindeluk M.Active control of waves in a timoshenko beam［J］.International Journal of Solids and Structures，2001，38(10-13):1749-1764.

［14］ Mei C，Mace B R.Wave reflection and transmission in timoshenko beams and wave analysis of timoshenko beam structures［J］.Journal of Vibration and Acoustics，2005，127(4):382-394.

［15］ MeiC. Hybrid wave/mode active controlofbending vibrations in beams based on the advanced timoshenko theory［J］.Journal of Sound and Vibration，2009，322(1-2):29-38.

［16］Pan X，Hansen C H.The effect of error sensor location and type on the active control of beam vibration［J］.Journal of Sound and Vibration，1993，165(3):497-510.