实时超声弹性成像原理与方法
孙瑞超 唐亚男 李灵 陆敏华,2,3 汪天富,2,3 陈思平,2,3
1 深圳大学医学院生物医学工程系(深圳 518060)
2 广东省生物医学信息检测与超声成像重点实验室(深圳 518060)
3 医学超声关键技术国家地方联合工程实验室(深圳 518060)
0.前言
生物组织的病变在很大程度上会伴随着其硬度属性的改变,比如硬化型乳腺癌,动脉粥样硬化等。然而在某些情况下,如果肿块较小,或者位置距离体表较深,用传统的触诊方式很难检测出。一般来说,用传统超声回波成像的方式,也并不一定能检测出这些癌变组织,因为虽然他们的硬度属性差别较大,但是声学性质有可能很相近。比如,对于前列腺或者乳腺肿瘤来说,他们用传统超声成像很难发现病变,但是他们的硬度属性和周围正常组织明显不同。所以组织硬度信息对于临床诊断而言同样具有重要的参考意义。超声弹性成像就是根据组织的硬度属性不同进行成像的一种新型的超声成像方式[1]。根据激励的时间特性,现有的基于超声检测的弹性成像可以分为三类:采用静态或准静态力的施压式弹性成像、采用低频瞬时振动的瞬时弹性成像和采用低频简谐波的震动声弹性成像。实际上,弹性成像(Elastography)一词,最早是1991年美国德州大学Ophir 教授等人提出[2],因此狭义上的弹性成像指的就是这种静态或准静态力施压式弹性成像。和其他两类相比较,准静态弹性成像具有技术原理简单,实时性好等优点,引起了很多研究组的兴趣,所以近几年得以迅速发展。本文重点在于介绍实时准静态超声弹性成像的原理与方法,同时还对模量重建的方法及其必要性进行了论述,最后讨论了评估一种新的弹性成像算法常用的验证方式。在下面的章节里,如无特殊说明,所提到的弹性成像均指准静态超声弹性成像技术。
1.技术原理
准静态超声弹性成像的实现方法如图1。
用超声探头对受检体施加一个外部的压力,接收同一个位置在施压前和施压后的两组回波信号。其中压缩后的信号可以视为压缩前信号的压缩和时延,如公式(1)所示[3]。
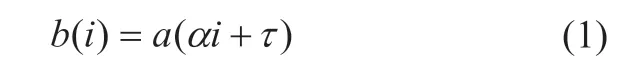

图1.准静态弹性成像框图
对同一个位置压缩前、后回波信号进行分析,得到应变分布;最后再用不同的灰阶值或者伪彩色等将组织应变的二维分布转化为二维的灰度或者伪彩色图像(strain-based elastography),其图像成为应变分布图(strain elastogram)。该方法中假设组织内部应力均匀分布,但对于血管等圆周应力分布明显不均匀的情况误差较大。另一种方法根据组织的力学特性以及求解出来的应变进行模量重建,根据杨氏模量或剪切模量进行成像(model-based elastography)[4]。
根据应变计算方法的不同可以概括为两类:基于梯度的方法,和直接计算应变;
1.1 直接法:
直接法中,直接通过对组织压缩系数进行计算得到应变。可以通过对压缩后的RF 信号设置一个初始伸展系数,然后求解相关性函数,或者计算相关相位。根据计算结果修正伸展系数,直到达到所期待的相关性[5],或者相移接近于零[6]。也可以通过最优化的方式,在代价函数里将伸展系数作为未知变量,通过最小化代价函数求的伸展系数[7,8]。根据伸展系数来求得应变。这种方法对信号相关性要求较高,而且对系统噪声比较敏感,所以较少采用。
1.2 基于梯度的方法:
基于梯度的方法首先计算回波信号压缩前、后在时域上的相对位移;根据相对位移利用差分的方法求出组织应变。
基于梯度的方法中,从压缩前后的RF 信号估计组织运动是最核心的部分,大多数的位移估计算法重点都是在轴向位移估计,尽管轴向压缩组织会产生三个方向的形变(轴向、侧向、和梯度方向),在一般应变成像中,只需要轴向位移就足够了。尽管也会考虑侧向和梯度方向,但仅限于帮助提高侧向位移估计的精度。侧向应变成像可以帮助重建泊松比等参数,但是远没有轴向应变更重要[9],所以在本文中不做过多讨论。
本文重点介绍基于梯度的方法原理以及在准静态超声弹性成像中的应用。首先介绍常用的位移估计基本算法,并介绍目前常用的对于基本算法的改进方式。然后介绍从位移中提取组织应变的原理和方法,并对模量重建的方法以及必要性进行了讨论,最后列出了对于一种新的算法一般采取的几种验证方式。
2.位移估计基本算法
现有的位移估计算法中,几乎所有的方法都用到了块匹配或者窗匹配。匹配的相似性准则包括:互相关,绝对差分和,平方差分和,相关相位等。窗匹配一般可以通过插值达到亚采样点精度;匹配可以在整个搜索区域内进行搜索,也可以通过相邻窗的连续性约束,减少搜索范围。可以通过定义一个全局代价函数,一次性求解位移场分布,也可以分块独立进行搜索跟踪。可以单层穷尽搜索,也可以分层从粗到细搜索。可以在整个平面两维搜索,也可以在轴向和侧向分别搜索[9]。
另外对现有位移估计算法进行严格划分是不科学的。很难把他们归结为某一种特定的方法名称里面。但通常所采用的基本技术主要包括几下几种:
2.1 一维时域互相关
一维互相关是计算时延常用的方法,通过对两段信号计算互相关函数,公式如(2)所示,当互相关函数取最大值时,τ 所代表的值就是两段信号的时延[2,10~13]。
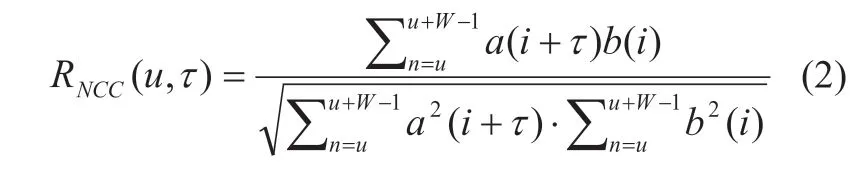
2.2 相关相位
超声射频信号不仅包含幅度信息,通过希尔伯特变换或者正交解调即可得到含有相位信息的解析信号或者是基带信号。在时域,时延对应着相位变化,如果信号频率已知,就可以根据计算相移直接得到相对应的时延[14~17]。
首先对于压缩前、后超声回波信号分别进行建模如公式(3),A(t)是包含人体信息的包络信号,w0 是探头的中心频率,t 是时间[14]。

这两个复数信号的互相关表达式可以表示为公式(4)
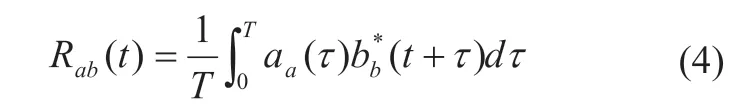
其中
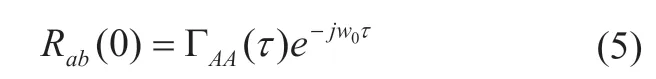
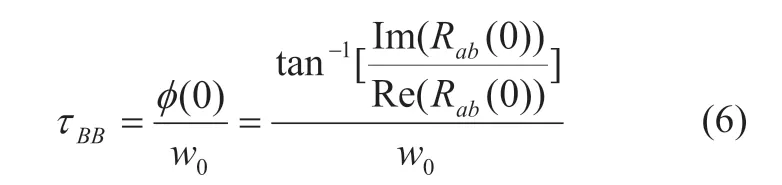
2.3 块匹配

图2.块匹配原理图(a)感兴趣窗,(b)搜索区域
块匹配的基本原理是对于感兴趣区域区内的一个特定大小的区块,在一个设定的搜索区域内根据一定的匹配准则寻找与它最佳匹配的区域。根据最佳匹配区域所在的位置来计算相邻两帧图像的局部位移[18~20]。
根据匹配准则的不同,可以分为:二维标准互相关,快速互相关,绝对差分和等。以二维互相关为例,其互相关函数定义为:

当上述函数取最大值时对应的u,v 的值,即是所定义区块中心位置的局部位移.
2.4 光流
光流法给空间每一个像素点赋予一个速度矢量,并假设空间任意一点 随时间变化该像素点的亮度不变[19,21]。即有下列等式:
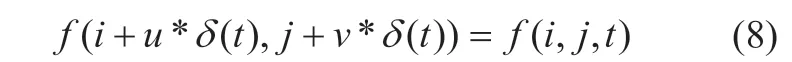
经过泰勒公式展开并去掉高阶部分可以得到:
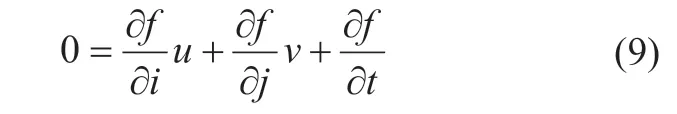
这就是光流的基本方程,实际应用中一般还要加上其他的约束条件,共同求解每个像素点的速度矢量(u,v)。根据外加约束条件的不同衍生出了不同的光流法。
2.5 最优化
最优化算法的基本原理是首先设计一个代价函数,通常是块匹配中几种匹配准则中的其中一种,或者加入另外的约束条件,组成复合的代价函数;其中代价函数所包含的未知参数通常就是所求的位移,甚至可以是应变。然后通过某种最优化算法如动态规划等进行求解[22~28]。最常见的代价函数具有以下形式:
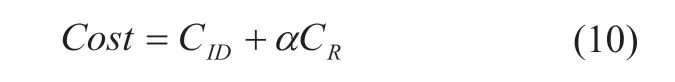
其中CID表示图像相似性,通常指定为块匹配准则中的某一项,CR表示另外的约束项,比如平滑约束或者位移连续性约束等。α表示权重系数,通过调整α可以调整每一项在代价函数中的权重。
对于检测信号相似性或者时延来说,互相关或者块匹配是非常精确的技术。即使应变很小的情况下,也可以精确追踪运动,并且对于噪声的鲁棒性较好。然而应变估计会受到各种因素的影响,包括探头下压过程的横向位移导致其不同平面运动造成的信号去相关,声场不均匀特性,非刚性组织形变等[21],导从而导致运动估计错误。另一方面,基于相位的方法是效率最高的,但是当时延大于半个波长的时候就会出现相位混叠,而且必须知道探头的中心频率,否则只能通过迭代来求解。光流暗含的假设信息是在连续记录的图像强度保持不变,然而在弹性成像过程中,散射点受压之后脉冲响应会发生变化。所以在光流法中通过局部信息约束进行求解是不科学的。一般会通过加入另外的全局约束信息来进行求解。另外基于相位的方法以及一维互相关方法只能在轴向进行追踪,当组织侧向位移较大时,会出现比较明显的位移估计错误。
上述基本算法除了基于相位的算法以外(依赖相位信息),其他所有算法都可以用三种信号来进行(RF 信号,包络信号,B 超信号)。包络信号可通过RF 信号正交解调得到,对包络信号进行对数压缩,去噪等处理就可以得到B 超信号。RF 信号的信息量最大,同时数据量也最大。B-mode 数据信息量和数据量都最小。随着弹性成像算法的不断发展,改进算法的速度越来越快,对于精度和分辨率的要求越来越高。目前准静态超声弹性成像大部分都是用RF 信号来计算的。
3.改进算法
由于人体组织的复杂性,以及超声图像本身所含的噪声等因素,单纯的采用上述基本算法,很难得到满意的结果。现有的方法中对于超声准静态弹性成像算法主要有两个思路:一种是基于其中一种算法,然后进行改进;另一种思路是集合两种或者以上的算法,形成一种新的算法框架,结合了各自的优势,同时克服了各自的不足。但无论是采用那一种思路,所进行的改进主要针对两个方面:速度和准确性(包括计算精度,和鲁棒性)。目前的改进技术主要包括以下几种:
3.1 时域伸展
基于梯度的算法一般都假设压缩后的信号是压缩前信号的时延,而忽略了形变(压缩)。所以当信号形变较大时,会出现比较严重的去相关[29]。Bai 等人,通过采用多尺度(multi-scale)的方式,采用不同长度的窗进行相关并求平均的方式进行改善[30]。通过自适应方法来计算局部压缩系数,可以降低信号去相关的影响,同时精度有所提高[5~28]。还可以通过扩张的方式在计算相关函数之前对信号进行调整,对压缩或者时延在同一个平面内进行调整,尽量恢复信号相关性[31]。但是,对于压缩的调整并不是自适应的,而是全局的。
3.2 插值
对于精确的应变估计,需要得到亚采样点间隔的位移场。一般通过对RF 信号进行插值,或者对相关函数进行插值,或者是假设峰值处形状,根据计算公式直接来得到。对RF 信号进行插值在很大程度上增加了运算量,对相关函数插值同样增加不小的计算量,常用的方法包括抛物线插值,余弦函数差值等[32]。而假设峰值处形状基本可以达到与差值RF 信号或相关函数同样的效果[33]。
3.3 先验估计或约束
由于信号的去相关,从信号直接求解位移分布可能会出问题,对于解决这种大的估计误差通常有两种途径[34]:运动约束或者先验搜索。
先验估计,也可以称为指导搜索,其基本原理是由周围已知点的位移值作为当前值的先验估计,相邻的点可以是相邻行的点,称为行引导,也可以是相邻列的点,称为列引导。也可以通过预先估计的方式来获得,一般通过由粗到细的方式来实现。根据先验估计可以缩小搜索范围,不但大大提高了计算速度,而且还在一定程度上减少了假的相关峰(当信号去相关比较严重时,峰值处的相关系数偏低,可能会出现另一处峰值并且相关系数大于真正的峰值,称为假峰)造成的估计错误。但是这种指导搜索有一个潜在的问题,就是如果有一个点估计错误,则基于该点作为先验值的所有位置都会产生错误估计。所以要通过某些机制来对估计结果进行验证,对于错误的点,通过周围点插值来替代。
运动约束也是目前比较常用的一种改进策略,主要是基于运动连续的假设[35]。一般是设计一个目标函数并添加约束项,然后通过最优化算法来最小化目标函数的方式来求解位移。由于运动约束把相邻点的位移值联系起来组成代价函数,所以单独分块进行估计显然达不到要求,一般通过全局最优化的方式来实现。
3.4 粗到细
由粗到细的原理是:首先选择一种鲁棒性较好的算法对复杂的位移场进行预估,估计结果作为另外一种鲁棒性较差但是精确度较高算法的先验值,或者初始值[9,19,27,36,37]。这样通过两步或者是几步迭代的方法同时满足了鲁棒性好,精确度高的要求。
在两步算法中,可以选择不同的基本算法,比如第一步选用块匹配,第二步采用光流[19];也可以采用同样的方法,但是不同的参数[37],比如两步都采用BMA 方法,但是第一步选择较大的窗和搜索范围,第二部选择较小的窗和较小的搜索范围。甚至两步里可以选择不同的信号,比如:第一步用B-mode 信号,第二部选择RF 信号。或者采用金字塔算法,从最底层到最高层依次降采样处理,减少数据量,通过某种算法得到位移场(BMA 或者图像配准)然后插值到与上一层相同的数据量,作为先验值,指导上一层在一个较小的范围内进行搜索[27,36]。
上述改进方法中,时域伸展技术可以解决信号压缩造成的信号去相关,但是对于其他原因的噪声,比如系统噪声或者非刚性形变造成的去相关没有效果,而约束和先验值对此则有比较明显的效果。插值主要是为了提高估计精度和质量,而由粗到细的策略是先验估计方法的一种具体实现方式。粗估计的结果作为细估计的先验值,从而使得速度和鲁棒性以及精确性都有较大的提高,所以这种方法也是最常用的一种方法。
4.应变
位移和应变的关系可以描为数值差分的过程。对于理想的全通差分器的频率响应,随着频率增大而线性增大,简单的差分过程会放大高频噪声。在应变求解过程中,应该设计一种低通的数字差分器,而不是全通的[38]。目前采用较多的最小二乘法也可以视为一种特殊的低通差分器[39,40]。
最小二乘法的原理是通过对位移场进行分段线性拟合来求出应变。计算公式如公式[39]:

其中y表示深度,u是位移,a,b是待估计的常量,其中,a表示局部应变。
采用低通数字差分器,应变值可以表示为位移场与特定冲击响应的卷积[40]:

另一种比较常用的差分器是Savitzky–Golay(SG)平滑数字差分器。根据拟合的阶数不同可以分为SG-I 和SG-II。以SG-I 为例,其输入输出关系为[38]:
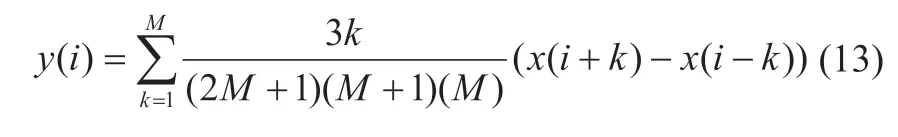
其中滤波器的长度为2M+1
确定滤波器的长度之后,就可以根据上述差分方程得到冲击响应h,h与位移u进行卷积就可以得到应变分布,最小二乘法也可以转化为上述形式。最小二乘法通过增加窗长以达到平滑的效果。较大的窗长可以得到比较好的SNR,但同时会造成边缘模糊。所以在实际运用的时候需要选择合适的窗长和窗之间的重叠率,以达到期待的效果。一般来讲为了平衡SNR 和CNR,推荐使用较长的滤波器长度以及较高的重叠率(90%以上)。对于不同数字差分器频率响应分析,与滤波器长度的关系,以及对应变估计的影响可参考文献[38]。
由于上述方法计算速度较快,是现有方法中计算应变较多采用的方法。然而,如果位移场估计不准确,应变估计会有较大噪声。Rivaz 等人,利用应变分段连续的特性,利用卡尔曼滤波器,来提高应变估计的质量[26]。Yuan 等人也采用了基于无网格的技术,在保持图像分辨率不变的前提下,对噪声进行抑制[41]。
5.杨氏模量
如果组织内部应力分布是常量,应变图像可以直接被解释为模量图像(杨氏模量或者剪切模量)。在实际情况下,内部应力分布并不均匀,所以当应变被解释为模量的过程中,会出现伪影,从而需要进行模量重建。模量重建可以根据计算的位移或者应变通过方程直接求解[42],也可以通过迭代的方式来进行求解。
比较常用的是通过模型迭代的方法来求解逆问题。该过程可以描述为参数最优化问题,通过最小化一个代价函数来得到参数最优解。其中,代价函数通常定义为测量位移和通过给定参数由有限元模型正向求解的位移差。通过对未知的杨氏模量给定初始值,然后以迭代的方式计算出代价函数最小时候杨氏模量的分布。
通过逆问题求解在一定程度上可以减少伪影,但是由于逆问题本身病态的特性,所以有可能增加新的伪影。当边界条件较简单时,逆问题求解对结果去除伪影的帮助并不大[43]。另一方面,逆问题求解通常需要通过反复迭代,很难达到实时。所以 目前的实时超声弹性成像一般都不包含这一步。
6.评价方法
对于一种新的弹性成像算法,如何评价其性能,有一些常用的方法。
6.1 数值仿真
用经过数值仿真产生的RF 信号来计算组织的应变分布,并将计算结果与有限元软件输出的应变分布作定量比较。仿真的方法如下
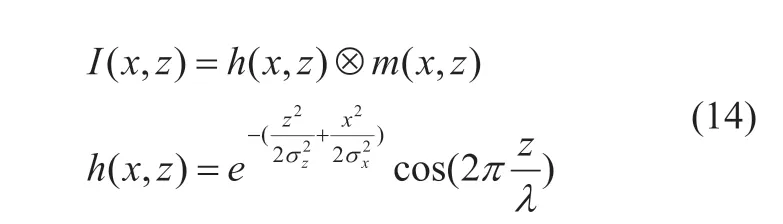

图3.数值仿真框图

图4.商用弹性体模
其中,x,z分别表示侧向和纵向,I(x,z)表示RF 信号,h(x,z)表示点扩散函数,m(x,z)表示声阻抗矩阵,A为常量,λ为发射脉冲波长,σx,σz分别为脉冲的宽度和长度。
在弹性成像中,对比度噪声比通常用来表征病变组织的可探测性。
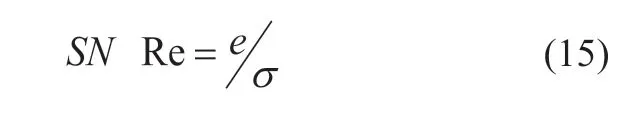
其中e和σ分别是均匀弹性组织应变图中的应变均值和应变标准方差。

eb,ei分别是应变图中背景和包含物的应变均值,分别是背景和包含物的应变方差。
6.2 弹性体模:
在弹性成像算法开发的初始阶段,体模实验是不可或缺的。首先,较好的弹性体模可以在声学和力学特性都和人体组织有较好的相似性。目前商用体模比较好的有CIRS 公司的Model049,以及Model059。其中,Model049 是在一个均匀的背景区域包含了8 个硬度和大小不同的小球,可以对弹性的分辨率和信噪比等参数做量化分析。
7.处理和显示
上述两种评价方法可用于算法研究人员在开发阶段作为参考。但是准静态超声弹性成像用于临床引用会出现各种复杂的问题:首先,对于医生的手法要求较高,很容易出现out-of-plane 现象;另一方面,病变组织的复杂程度远高于弹性体模,所以在算法真正实现的过程中一般还要经过一些处理。最常用的是进行归一化处理[44]。
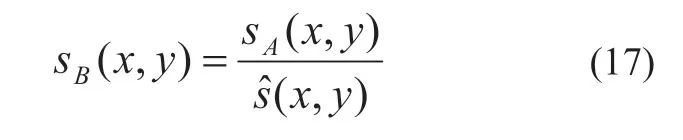
ŝ(x,y)是归一化系数,最简单的方式是设为常量,取图像中的最大应变值,从而消除不同的应变率对显示结果的影响。对于内部应力分布不均(随着深度降低,或者探头表面压力不均造成)对应变的影响,可以设置整个平面随位置变化的归一化系数。归一化系数通过对位移场或者应变进行平面拟合的方式求解。
由于在临床操作中,应变大小控制、探头偏移等问题,采用两帧信号得到的应变图信噪比通常不高。所以在临床使用过程中,通常会用相邻的应变图像拟合成一幅高质量的图像进行显示。这种拟合可以是简单的平均[45],也可以根据应变图中每个点的估计质量来进行加权合成[4,44]。
8.总结
准静态超声弹性成像技术,自上世纪90年代初被提出来,至今已经过了20年的发展历程。该技术到目前为止已经较为成熟,并且进入了商用化阶段。近几年带有弹性成像功能的医用超声系统越来越多,目前多数是国外产品,价格较高。近年汕头市超声仪器研究所有限公司和深圳迈瑞医疗电子有限公司相继突破了该项技术,在其超声系统上实现了国产的实时弹性成像方法。本文对实时超声弹性成像原理和方法进行介绍,内容包括了准静态超声弹性成像中绝大部分常见概念,尤其对常用基于梯度的应变成像中,位移估计算法,以及应变估计算法,做了详细叙述,分析了各自的优缺点,并对模量重建的方法及其必要性进行了论述,最后讨论了评价一种新的弹性成像算法常用的验证方式。
[1].Ophir J,Alam SK,Garra B,Kallel F,Konofagou E,Krouskop T,Varghese T:Elastography:ultrasonic estimation and imaging of the elastic properties of tissues.Proceedings of the Institution of Mechanical Engineers,Part H:Journal of Engineering in Medicine 1999,213(3):203-233.
[2].Ophir J,Cespedes I,Ponnekanti H,Yazdi Y,Li X:Elastography:a quantitative method for imaging the elasticity of biological tissues.Ultrasonic imaging 1991,13(2):111-134.
[3].Ramalli A,Basset O,Cachard C,Tortoli P:Quasi-static elastography based on high frame-rate imaging and frequency domain displacement estimation.In:Ultrasonics Symposium(IUS),2010 IEEE:2010:IEEE;2010:9-12.
[4].Treece G,Lindop J,Chen L,Housden J,Prager R,Gee A:Real-time quasi-static ultrasound elastography.Interface Focus 2011,1(4):540-552.
[5].Alam SK,Ophir J,Konofagou EE:An adaptive strain estimator for elastography.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 1998,45(2):461-472.
[6].Brusseau E,Perrey C,Delachartre P,Vogt M,Vray D,Ermert H:Axial strain imaging using a local estimation of the scaling factor from RF ultrasound signals.Ultrasonic imaging 2000,22(2):95-107.
[7].Liu K,Zhang P,Shao J,Zhu X,Zhang Y,Bai J:A 2D strain estimator with numerical optimization method for soft-tissue elastography.Ultrasonics 2009,49(8):723-732.
[8].Deprez JF,Brusseau E,Schmitt C,Cloutier G,Basset O:3D estimation of soft biological tissue deformation from radio-frequency ultrasound volume acquisitions.Medical image analysis 2009,13(1):116.
[9].Chen L,Housden RJ,Treece GM,Gee AH,Prager RW:A hybrid displacement estimation method for ultrasonic elasticity imaging.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2010,57(4):866-882.
[10].Zahiri-Azar R,Salcudean SE:Motion estimation in ultrasound images using time domain cross correlation with prior estimates.Biomedical Engineering,IEEE Transactions on 2006,53(10):1990-2000.
[11].Zhang D,Zhang S,Wan M,Wang S:A fast tissue stiffness-dependent elastography for HIFU-induced lesions inspection.Ultrasonics 2011.
[12].Konofagou EE,Ophir J:Precision estimation and imaging of normal and shear components of the 3D strain tensor in elastography.Physics in Medicine and Biology 2000,45(6):1553.
[13].Konofagou E,Ophir J:A new elastographic method for estimation and imaging of lateral displacements,lateral strains,corrected axial strains and Poisson’s ratios in tissues.Ultrasound in medicine &biology 1998,24(8):1183-1199.
[14].O'Donnell M,Skovoroda AR,Shapo BM,Emelianov SY:Internal displacement and strain imaging using ultrasonic speckle tracking.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 1994,41(3):314-325.
[15].Cohn NA,Emelianov SY,Lubinski MA,O'Donnell M:An elasticity microscope.Part I:methods.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 1997,44(6):1304-1319.
[16].Shiina T,Nitta N,Ueno E,Bamber JC:Real time tissue elasticity imaging using the combined autocorrelation method.Journal of Medical Ultrasonics 2002,29(3):119-128.
[17].Pesavento A,Perrey C,Krueger M,Ermert H:A time-efficient and accurate strain estimation concept for ultrasonic elastography using iterative phase zero estimation.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 1999,46(5):1057-1067.
[18].Zhu Y,Hall TJ:A modified block matching method for real-time freehand strain imaging.Ultrasonic imaging 2002,24(3):161-176.
[19].Zhou Y,Zheng YP:A motion estimation refinement framework for real-time tissue axial strain estimation with freehand ultrasound.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2010,57(9):1943-1951.
[20].Luo J,Konofagou EE:A fast normalized cross-correlation calculation method for motion estimation.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2010,57(6):1347-1357.
[21].Pellot-Barakat C,Frouin F,Insana MF,Herment A:Ultrasound elastography based on multiscale estimations of regularized displacement fields.Medical Imaging,IEEE Transactions on 2004,23(2):153-163.
[22].Jiang J,Hall TJ:A generalized speckle tracking algorithm for ultrasonic strain imaging using dynamic programming.Ultrasound in medicine &biology 2009,35(11):1863.
[23].Jiang J,Hall TJ:6F-3 A Regularized Real-Time Motion Tracking Algorithm Using Dynamic Programming for Ultrasonic Strain Imaging.In:Ultrasonics Symposium,2006 IEEE:2006:IEEE;2006:606-609.
[24].Rivaz H,Boctor E,Foroughi P,Zellars R,Fichtinger G,Hager G:Ultrasound elastography:a dynamic programming approach.Medical Imaging,IEEE Transactions on 2008,27(10):1373-1377.
[25].Rivaz H,Boctor EM,Choti MA,Hager GD:Real-time regularized ultrasound elastography.Medical Imaging,IEEE Transactions on 2011,30(4):928-945.
[26].Rivaz H,Boctor E,Choti M,Hager G:Real-time regularized ultrasound elastography.Medical Imaging,IEEE Transactions on 2010(99):1-1.
[27].Liang Y,Zhu H,Friedman MH:Measurement of the 3D arterial wall strain tensor using intravascular B-mode ultrasound images:a feasibility study.Physics in Medicine and Biology 2010,55:6377.
[28].Brusseau E,Kybic J,Deprez JF,Basset O:2-D locally regularized tissue strain estimation from radio-frequency ultrasound images:Theoretical developments and results on experimental data.Medical Imaging,IEEE Transactions on 2008,27(2):145-160.
[29].Varghese T,Ophir J:Enhancement of echo-signal correlation in elastography using temporal stretching.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 1997,44(1):173-180.
[30].Bai J,Ding C,Fan YU:A multi-scale algorithm for ultrasonic strain reconstruction under moderate compression.Ultrasonics 1999,37(7):511-519.
[31].Chaturvedi P,Insana MF,Hall TJ:2-D companding for noise reduction in strain imaging.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 1998,45(1):179-191.
[32].Kim S,Aglyamov SR,Park S,O'Donnell M,Emelianov SY:An autocorrelation-based method for improvement of sub-pixel displacement estimation in ultrasound strain imaging.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2011,58(4):838-843.
[33].Lopata RGP,Nillesen MM,Hansen HHG,Gerrits IH,Thijssen JM,de Korte CL:Performance evaluation of methods for twodimensional displacement and strain estimation using ultrasound radio frequency data.Ultrasound in medicine &biology 2009,35(5):796-812.
[34].Jiang J,Hall TJ:A fast hybrid algorithm combining regularized motion tracking and predictive search for reducing the occurrence of large displacement errors.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2011,58(4):730-736.
[35].Liu W,Ribeiro E:A survey on image-based continuum-body motion estimation.Image and Vision Computing 2011,29(8):509-523.
[36].Shi H,Varghese T:Two-dimensional multi-level strain estimation for discontinuous tissue.Physics in Medicine and Biology 2006,52(2):389.
[37].Chen H,Shi H,Varghese T:Improvement of elastographic displacement estimation using a two-step cross-correlation method.Ultrasound in medicine &biology 2007,33(1):48.
[38].Luo J,Bai J,He P,Ying K:Axial strain calculation using a low-pass digital differentiator in ultrasound elastography.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2004,51(9):1119-1127.
[39].Kallel F,Ophir J:A least-squares strain estimator for elastography.Ultrasonic imaging 1997,19(3):195-208.
[40].Lindop J,Treece G,Gee A,Prager R:The general properties including accuracy and resolution of linear filtering methods for strain estimation.Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions on 2008,55(11):2363-2368.
[41].Yuan J,Zhang H,Lu M,Chen S,Liu H:A strain-based ultrasound elastography using phase shift with prior estimates and meshfree shape function.In:2011:IEEE;2011:532-535.
[42].Raghavan KR,Yagle AE:Forward and inverse problems in elasticity imaging of soft tissues.Nuclear Science,IEEE Transactions on 1994,41(4):1639-1648.
[43].Doyley MM,Srinivasan S,Pendergrass SA,Wu Z,Ophir J:Comparative evaluation of strain-based and model-based modulus elastography.Ultrasound in medicine &biology 2005,31(6):787-802.
[44].Lindop JE,Treece GM,Gee AH,Prager RW:An intelligent interface for freehand strain imaging.Ultrasound in medicine &biology 2008,34(7):1117-1128.
[45].Jiang J,Hall TJ,Sommer AM:A novel image formation method for ultrasonic strain imaging.Ultrasound in medicine &biology 2007,33(4):643.