静定梁受弯构件的转角与挠度的求解方法探讨

林相刚 焦安梅（日照港集团有限公司，山东 日照 276826）

在实际工程中，常常对梁和轴等受弯构件的变形有一定的限制要求，准确的计算梁或轴的转角及挠度，不仅可以做到安全有保障，而且能够最大限度的发挥材料的性能，有效降低成本。本文介绍受弯构件任意截面处位移和转角的常用计算方法，包括积分法、间断函数法、叠加法和静矩—面积法。

1 求梁位移和转角的积分法

在计算梁或轴任意截面处的位移和转角前，若能够根据梁的受力特点，定性画出梁挠曲线的大致形状，可直观的展示弯曲变形的计算结果，并有助于判断计算结果是否正确。梁弯曲后的轴线，即梁截面形心的连线，成为梁的挠曲线。一般地，施加约束力的约束（如铰）会限制梁在该处的线位移。而产生约束力偶的约束（如固定端）会同时限制梁在该处的旋转或转角及线位移。

弯矩-曲率关系（推导过程略）

其中

ρ=挠曲线上任意一点处的半径

M=梁上需要确定ρ值处的截面上的弯矩

E=材料的弹性模量

I=梁横截面对其中性轴的惯性矩

ν=f(x)梁挠曲线的数学表达式为[1]，由高等数学相关知识可得：

实际工程中多数梁或轴的挠曲线通常是一条非常平坦的曲线，于是 非常小，其平方更是远小于1，可忽略不计，所以曲率可近似的表示为

对（2）式求导可得

对（3）式求导可得

通过对上述任一微分方程多次积分，可得梁挠曲线上各点的挠度ν，同理可近似求得各点的转角θ（推导过程略）

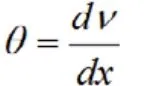
分析步骤

1）挠曲线

画梁挠曲线大致形状示意图：注意固定端处转角和位移均为零，而固定和活动铰支座处的位移为零。

建立x,ν坐标轴。x轴必须平行于梁变形前的轴线，原点为梁上任意一点，正向即可向右也可向左。

当梁上作用多个不连续载荷时，可在各间断点之间分段建立x坐标轴，以便使计算过程更加简洁。

任何情况下均要求ν坐标轴向上为正。

2）荷载方程或弯矩方程

写出梁在每一段中的荷载w或弯矩M随其中x坐标变化的函数。要特别注意利用平衡方程确定弯矩方程M=f(x)时，总是假设任意横截面上的弯矩的符号为正。

3）转角和挠曲线

若EI是常量，可利用含有荷载的方程EId4v/dx4=-w(x)，经过四次积分的到挠曲线方程ν=ν(x)；或者利用含有弯矩的方程EId2v/dx2=M(x)，只需经过两次积分即可获得挠曲线方程。注意每次积分过程中，不要遗漏积分常数。

积分常数由相关支座处的边界条件（可查阅相关图表）以及相邻挠曲线交界点转角和位移的连续条件确定。求出积分常数并带回梁的转角方程及挠曲线方程后，就可以计算梁上指定点的位移和转角。

可通过与挠曲线大致形状的示意图相比较检查计算结果。注意：坐标轴x取向右为正，转角逆时针为正；坐标轴x取向左为正时，转角顺时针转向为正。但在上述两种情况下，梁的位移v均取向上为正。

2 求梁的转角和位移的间断函数法

对于受弯构件，当其载荷或弯矩方程在整个梁的长度上都能用一个连续的函数表示时，采用积分法可以方便的求解梁的挠曲线方程。但是梁上作用多个不同的荷载时，由于需要分别求出每一段梁上各自独立的荷载或弯矩方程，并且还需要利用边界条件和连续条件确定积分常数，所以积分法会变得十分冗繁。本方法可只利用边界条件确定积分常数，不涉及梁变形的连续条件，求解过程将变得十分简洁，此方法需要用到两个函数：

麦考利函数[3]：该函数用来描述梁上的分布荷载，其表达式为

上式中，x是梁上一点的坐标，a表示梁上“间断点”出现的位置，即分布载荷的起点。注意麦考利函数n中的尖括号，以区别普通函数(x-a)n。只有当x>=a时，n=(x-a)n，否则其值为零。另外，只有当指数n>=0时，这些函数才成立。麦考利函数的积分规则与普通函数相同，即：

奇异函数[3]：奇异函数用来描述作用于受弯构件上一点的集中力或集中力偶。集中力P可以看成是一个特殊的分布载荷，其载荷集度为w=P/ε，而其分布区间趋近于零。此分布载荷与坐标轴x所围的面积等于P的大小，取向下为正。因此集中力P的值可用间断函数表示为：

注意，这里取n=-1,是为了使分布荷载的集度的量纲仍然为单位长度上的力，由此函数可知，只有在力的作用点x=a处，其值等于P，否则为零。

同样，对于集中外力偶M0,取逆时针为正，可以看成两个分布区间ε均趋于零的分布载荷，集中外力偶M0的值可用奇异函数表示为：

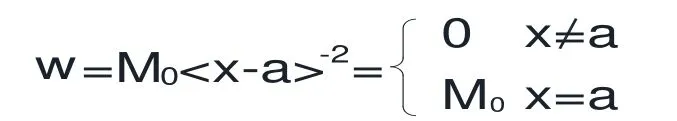
上式中n=-2，是为了保证此分布载荷集度的量纲仍然是单位长度上的力

上述两个奇异函数可按照算符运算规则进行积分，并得到与麦考利函数积分不同的结果，具体结果为

其中，积分后只是指数增加1，没有积分常数。利用上述公式，将集中力P或集中力偶M0，分别积分一次和两次后即可获得梁的剪力和弯矩。特别注意的是，集中力和分布载荷取下为正，集中外力偶取逆时针为正。

分析步骤

1）挠曲线

绘制挠曲线的大致形状，明确支座处的边界条件。

固定铰支座及活动铰支座处的位移为零，固定端处的转角和位移均为零。

建立坐标轴x,向右为正，原点在梁的左端。

2）载荷和弯矩方程

根据平衡方程，计算支座反力，将载荷w或弯矩M表示为x的函数，确保其中每一个载荷的符号都符合相应的约定。

注意分布载荷应满布至梁的最右端，否则需用叠加法使之成为满布分布载荷。

3）转角和挠曲线

将荷载w的方程代入EId4v/dx4=-w(x)或将弯矩M的方程代入EId2v/dx2=M(x)，积分后即可获得梁的转角和挠曲线方程。

根据边界条件计算积分常数，并将其值代回到转角和挠曲线方程，获得最终结果。

计算梁上任意一点处的转角和挠度时，总取转角逆时针为正，位移向上为正。

3 求梁的转角和位移的静矩—面积法

静矩—面积法提供了一种应用图解法求受弯构件某指定位置转角和位移的方法。这种方法需要计算与梁的弯矩图有关的面积。因此当弯矩图比较简单时，如梁上作用集中力或力偶时，这种方法将会十分简洁。此种方法需要用到两个定理（推导过程略）。

定理1[3]挠曲线上任意两点的切线之间的夹角大小等于该两点M/EI图所围的面积。

定理2[3]挠曲线上任意一点A处切线相对于另-任意点B处切线的垂直方向偏差tA/B,等于这两点M/EI图所围面积对点A的静矩。

分析步骤

M/EI图

确定梁的约束反力，作梁的M/EI图。若梁上只作用集中力，则M/EI图将由若干个直线段组成，应用两个静矩—面积定理，所需计算的图形面积和静矩将比较简单。当梁上作用若干个分布载荷时，M/EI图将由抛物线或更复杂的高阶曲线组成，此时建议查材料力学相关附录计算图形的面积和形心。

2）挠曲线

画挠曲线的大致形状。注意，梁上固定端的转角和位移均为零，固定和活动铰支座处的位移为零。

当直接绘制挠曲线的大致形状比较难时，可借助弯矩图。切记，梁横截面上作用正弯矩时，挠曲线为向下凸的曲线；当作用负弯矩时，挠曲线为向上凸的曲线；在弯矩等于零的地方，挠曲线有拐点。

将需要求解的转角和位移标在挠曲线上。

静矩—面积定理只是用来确定挠曲线上任意两点切线间的夹角和偏差。因此，为了利用两切线间的夹角和位移求解问题，应注意首先选择恰当的点作切线。通常支座处的位移或转角位零，所以应选择支座处作切线。

3）静矩—面积定理

利用定理1求挠曲线上两点切线间的夹角，利用定理2求切线间的相对偏差。

根据挠曲线示意图上的夹角和偏差，校核结果的符号是否正确。

正的θB/A值说明B点切线相对于A点为逆时针转向，正的tB/A值说明挠曲线上B点位于由A点所作切线的上方。

4 求梁的转角和位移的叠加法

当构件上作用多个荷载时，可用叠加法求其变形。若由某载荷单独作用时引起的位移为v1,另一载荷单独作用时引起的位移为v2,则在这两个载荷共同作用下的位移等于这两个载荷单独作用时位移的代数和v1+v2。受弯构件在各种单独载荷作用下的变形可由以上三种方法予以求解，亦可查阅相关工程设计手册。当梁承受多个载荷时，可以将每个力单独作用的结果进行代数叠加，求得梁上某指定点的转角和位移。

5 结语

本文介绍的四种求静定梁的转角和位移的方法，在机械、土木、水利等行业均有很强的实用性，只是不同的行业，对梁的转角和位移的控制精度不同，采用的材料也不尽相同，也就是说材料的弹性模量不同，但是解决问题的思路是一样的。

[1] 高等数学 同济大学数学教研室主编 高等教育出版社，1998重印，218-221

[2] 钢结构设计与计算 包头钢铁设计研究院，中国钢结构协会房屋建筑钢结构协会编著.北京-机械工业出版社，2000.3,474

[3] 材料力学 希伯勒 著； 汪越胜等译.- 北京：电子工业出版社，2006.8 481-491