新拌自密实混凝土工作性试验及其综合评价
刘华良 屈慧琼 石建军 邓仕军
(1南华大学城市建设学院,湖南 衡阳421001;2南华大学核资源工程学院,湖南 衡阳421001)
自密实混凝土(Self Compacting Concrete,又称为Self Consolidating Concrete,简称SCC),是当今高性能混凝土的重要发展方向[1],其配合比与混凝土工作性能、物理力学性能具有紧密联系,科学评价自密实混凝土配合比方案具有一定的理论和现实意义。但由于自密实混凝土组分复杂多样,各组分之间又相互影响、相互制约,其拌和物的工作性能很难用单因素的回归关系加以描述,且工作性的测定方法众多,评定指标各异,有些指标可量化而有些非量化。因此,如何从有限的自密实混凝土工作性试验样本数据中评判优劣和确定优选配合比方案是一个难题。本文在自密实混凝土工作性试验的基础上,基于层次分析法基本原理,构建了一个对自密实混凝土工作性能综合评价和优化选择的层次分析模型。
1 自密实混凝土工作性试验
1.1 原材料
在本试验中,采用了如下材料:
1)胶凝材料:衡阳市“世达”牌水泥(32.5R),该水泥有较低的水化热,经试验与外加剂的相容性较好。
2)粉煤灰掺合料
湘潭II级粉煤灰,具有低用水量和高活性的性能,其技术性能和化学成分如表1。

表1 湘潭粉煤灰的化学成分
3)骨料
采用普通的粗骨料,粒径范围为5~10mm和5~20mm的卵石(衡阳地区),其表观密度ρ=2.7g/cm3;细骨料为级配良好的中粗砂,细度模数2.4。
4)外加剂
聚羧酸盐高效减水剂,该外加剂有减水、增塑的双重作用,坍落度损失低,低掺量,不缓凝,与掺加时间的先后关系不大。
5)水
衡阳地区普通自来水。
1.2 配合比
本文试验采用三种自密实混凝土样本,编号分别为D1、D2和D3,其配合比见表2。
1.3 工作性试验方法
通过坍落扩展度试验、V型漏斗实验来测试自密实混凝土的流动性和充填能力,通过J-ring实验来测试间隙通过能力,通过VSI目测方法测试抗离析能力。
1.4 试验结果
三种自密实混凝土样本的工作性实验数据如表3所示。
2 层次分析法基本原理与步骤[2-5]
层次分析法是20世纪70年度由美国学者T.L.Saaty提出的一种定性与定量分析相结合的多目标决策方法[2]。层次分析法假设层次之间存在递进结构,即从高到低或从低到高递进,其基本思想是把复杂问题分解为若干层次,在最低层次通过两两对比得出各因素的权重,通过由低到高的层层分析计算,最后计算出各方案对总目标的权数,权数最大的方案即为最优方案[3][4]。
2.1 建立递阶层次结构

表2 三种自密实混凝土配合比(单位:kg/m3)

图1 坍落扩展度试验

图2 V漏斗试验

图3 J-ring试验

图4 VSI对比试验

表3 新拌自密实混凝土工作性能试验结果
应用AHP分析决策问题时,首先要把问题条理化、层次化,构造出一个自上而下的支配关系所形成的层次结构,称为递阶层次结构。典型的层次结构表示如图5。
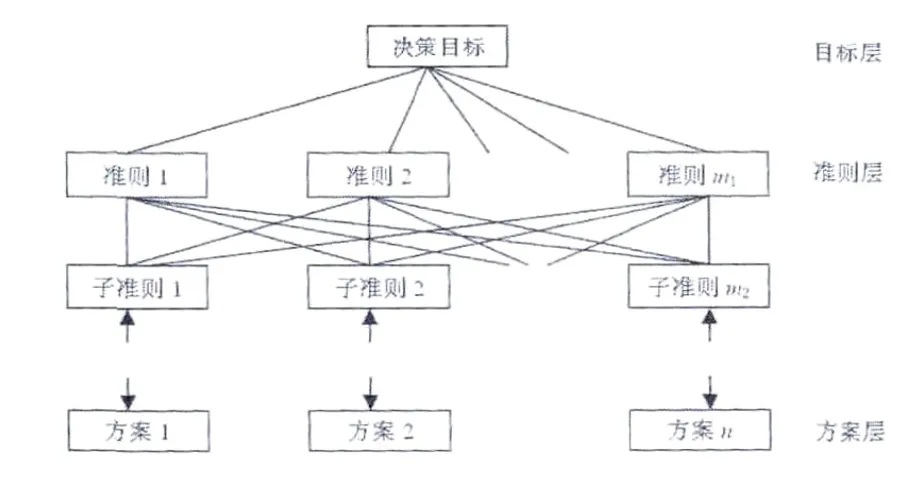
图5 递阶层次结构示意图
2.2 构造判断矩阵
判断矩阵是层次分析法的核心,其元素aij可以利用决策者的知识和经验估计出来,Saaty建议引用数字1~9及其倒数作为标度来表征重要性,其标度方法见表4。
2.3 层次单排序及一致性检验
判断矩阵A对应于最大特征值λmax的特征向量W,经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值,这一过程称为层次单排序。对决策者提供的判断矩阵有必要作一次一致性检验,以决定是否能接受它。
1)权重计算
由各层判断矩阵确定各层权重。如利用根法将判断矩阵A的各个行向量进行几何平均,然后归一化,得到的行向量就是权重向量。其公式为

2)计算一致性指标CI(consistency index)

其中

3)查平均随机一致性指标RI(random index)。对n=1,∧,9,Saaty给出了RI的值(表2)。
4)计算一致性比例CR (consistency ratio)

2.4 层次总排序及一致性检验
最终得到最低层中各方案对于目标的排序权重,从而进行方案选择。总排序权重要自上而下地将单准则下的权重进行合成。
设上一层次(A层)包含A1,…Am共m个因素,它们的层次总排序权重分别为a1…am,又设其后的下一层次(B层)包含n个因素B1,…Bn,它们关于Aj的层次单排序权重分别为b1…bn,(当Bi与Aj无关联时,bij =0)。现求B层中各因素关于总目标的权重,即求B层各因素的层次总排序权重b1…bn。

表4 判断矩阵标度及其含义
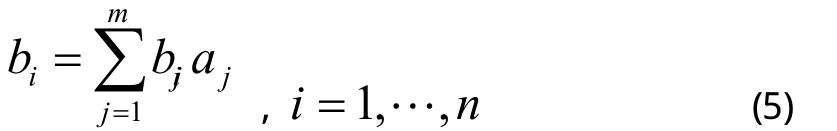
对层次总排序也需作一致性检验,检验仍象层次总排序那样由高层到低层逐层进行。设B层中与Aj相关的因素的成对比较判断矩阵在单排序中经一致性检验,求得单排序一致性指标为CR(j),(j=1,…m),相应的平均随机一致性指标为RI(j),则B层总排序随机一致性比例为

2.5 方案评价
计算每一层的权重矩阵,对应相乘得到各方案关于总目标的权重。各方案依关于总目标的权重大小按顺序排成一列,具有最大权重的方案就是最优方案。
3 新拌SCC工作性层次分析评价
3.1 建立层次结构模型
借助于层次分析法原理,建立图6所示层次结构模型图。其中,第一层为目标层新拌SCC工作性评价A,用于SCC拌合料工作性能的评价;第二层为准则层,包括充填能力B1、间歇通过能力B2、抗离析能力B3,是评价的基本原则和依据;第三层是子准则层,或者叫指标层,包括坍落度C1、扩展度C2、T500C3、V型漏斗试验C4、L-boxC5、U-boxC6、J-ringC7、箱型填充试验C8、贯入试验C9、浆体筛分法C10、VSIC11,是上一级准则的细化;第四层是自密实混凝土配合比方案层,包括D1、D2和D3。

表5 平均随机一致性指标
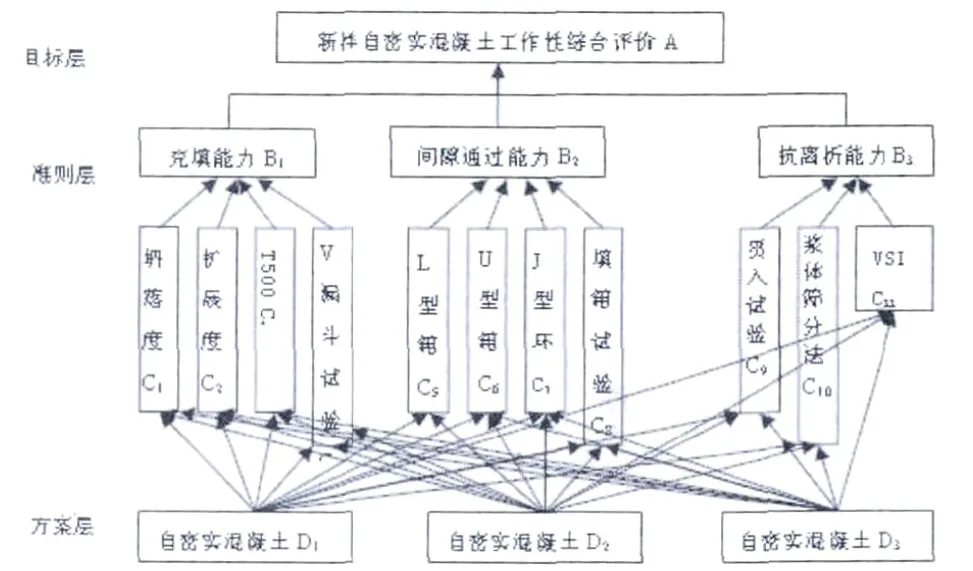
图6 新拌自密实混凝土工作性综合评价层次结构模型
3.2 构建判断矩阵
参照国内外自密实混凝土规范,根据专家打分,构建新拌自密实混凝土工作性综合评价层次结构模型的判断矩阵如表6至表9,并按上述相关公式计算出判断矩阵的各权重值ωi。采用方根法计算判断矩阵的最大特征值及特征向量。
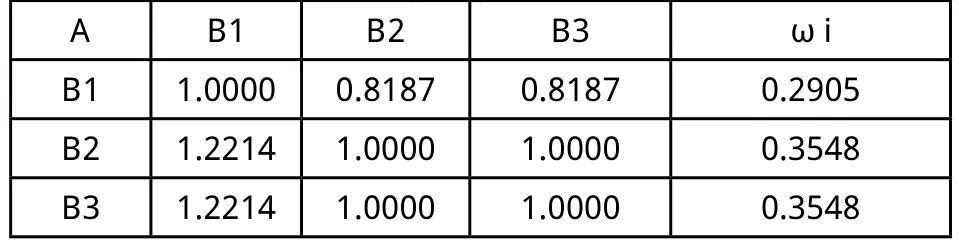
表6 (A-B)判断矩阵

表7 (B1-C)判断矩阵
3.3 层次单排序及一致性检验
计算出判断矩阵权向量W和一致性比例CR(见表10)。经检验,所构造的各个判断矩阵均具有满意的一致性,说明权数分配合理。
3.4 层次总排序及一致性检验
计算出目标A下,C1—C11的组合权重如表11。进行目标总排序一致性检验如下,可见层次总排序满足一致性要求。


表8 (B2-C)判断矩阵
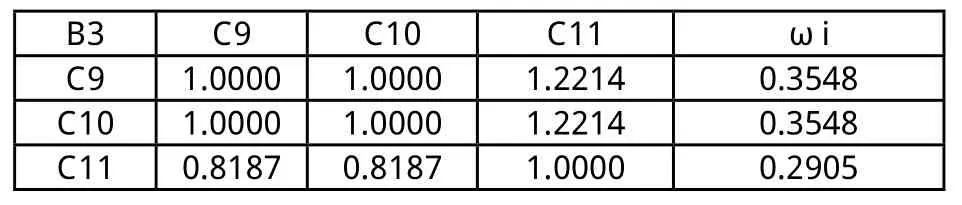
表9 (B3-C)判断矩阵
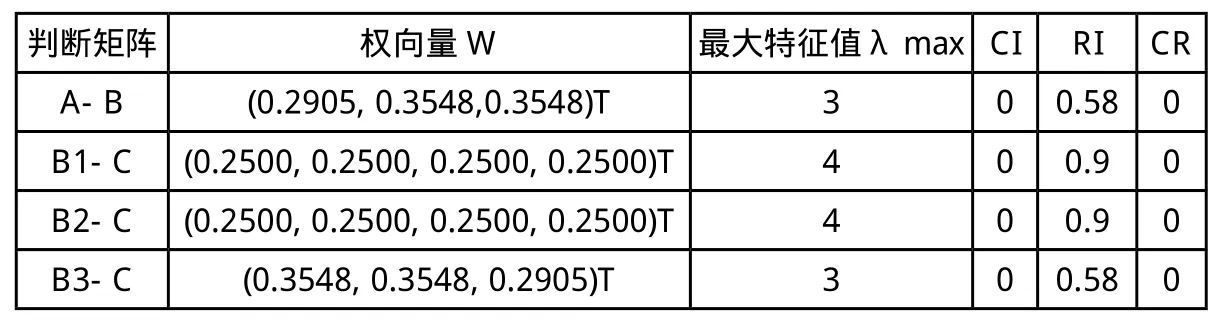
表10 判断矩阵特征值
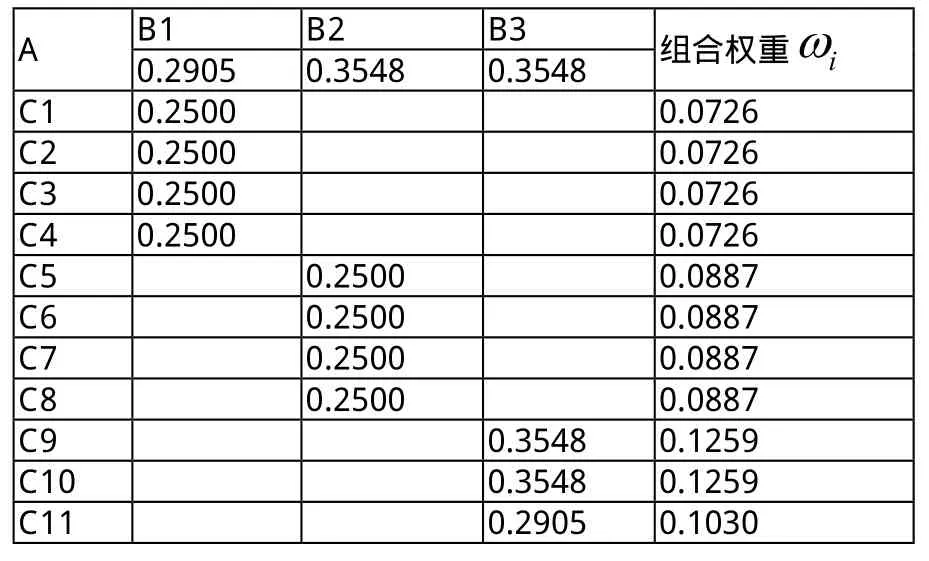
表11 A—C的组合权重
4 评价模型的应用
现参照参考文献[6],表2和表6评价指标,应用层次分析法模型,对以上D1、D2和D3三种自密实混凝土配合比进行综合评价和优选。
1)分析D1、D2、D3三种自密实混凝土的充填能力:根据表3中所列实验数据,建立(C1—D)、(C2—D)、(C3—D)、(C4—D)四组判断矩阵,分别如表12-表15所示,并计算出相应权重值。由权重向量组成权重矩阵,再与(B1-C)判断矩阵相乘可得到B1—D的组合权重(如表16所示),分析结果显示在SCC充填能力方面D1>D3>D2。
2)分析D1、D2、D3三种试样其他工作性能(间歇通过能力和抗离析能力):因为限于实验条件,在间隙通过能力测试方面只做了J-ring实验,在抗离析能力测试方面只做了VSI实验,实验数据并不完整,因此在第1步前提下,根据表3中所列实验数据,只是再建立(C7—D)、(C11—D)两组判断矩阵,分别见表17、表18,并计算出相应权重值。再与(A-C)判断矩阵相乘可得到A—D的组合权重(0.2125、0.1164、0.1533)T(如表19所示),分析结果显示在SCC综合工作性能方面D1>D3>D2。

表12 (C1-D)判断矩阵

表13 (C2-D)判断矩阵
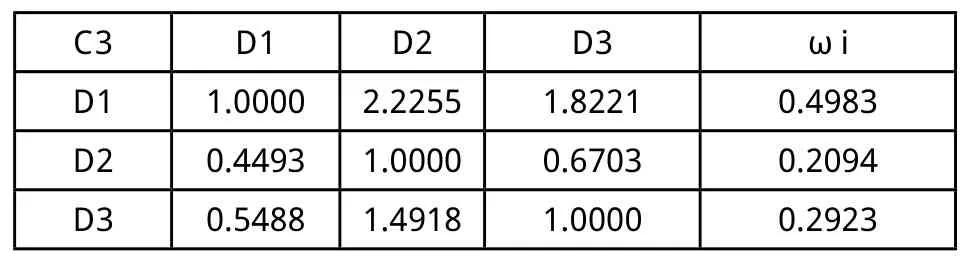
表14 (C3-D)判断矩阵
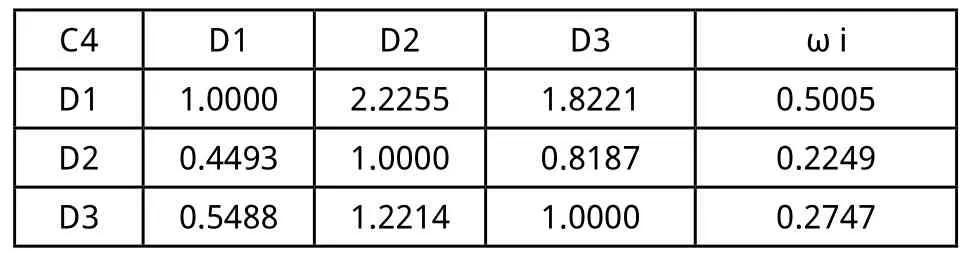
表15 (C4-D)判断矩阵
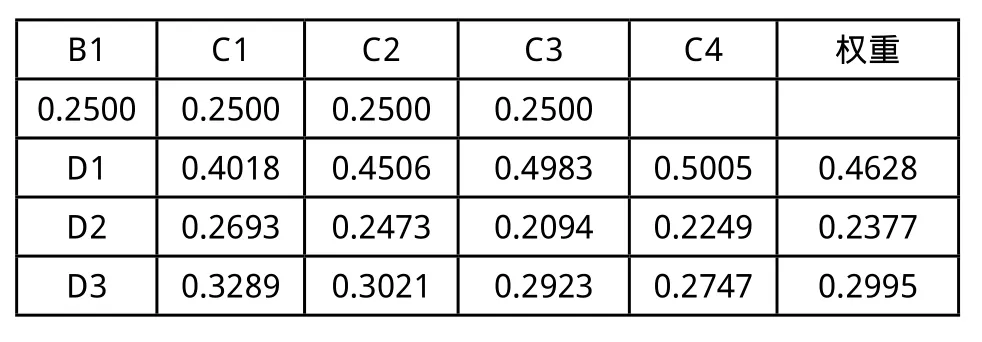
表16 B1-D的组合权重
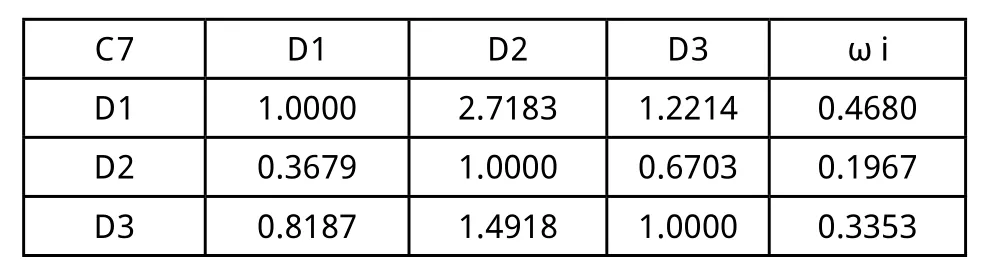
表17 (C7-D)判断矩阵
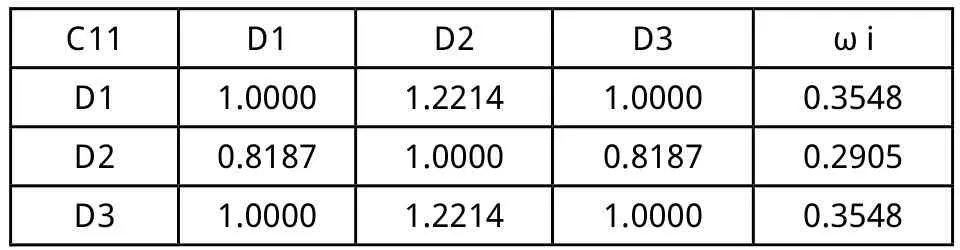
表18 (C11-D)判断矩阵
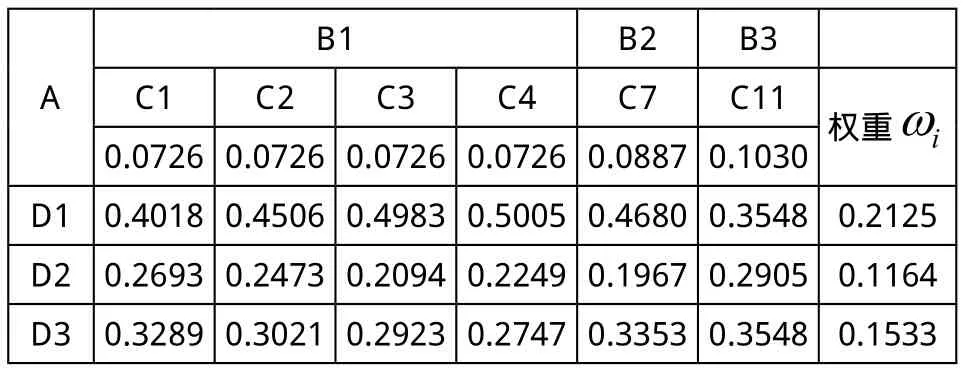
表19 A—D的组合权重

表20 A—D的组合权重
另外,假定三种试样中,未做实验的各项性能参数没有差别,也就是在(Ci—D)判断矩阵(Ci为未做的实验)中算得的权重向量均为(0.3333 0.3333 0.3333)T,则算得最终A—D的组合权重为(0.3851 0.2890 0.3259)T(如表20所示),结论与前者完全一致。
4 结语
通过该模型计算得出,自密实混凝土配合比方案优劣排序为:D1>D3>D2,设计时,选择D1方案。这一结论也从混凝土试样轴压强度和弹性模量(见表3)得到了印证。
应用层次分析法原理建立的新拌自密实混凝土工作性综合评价模型具有简单实用的特点,能比较全面、准确、科学地评价新拌SCC的工作性能,从而利于从众多配合比方案中选择最佳方案。
[1]Okamura H,Ouchi M.Self-compacting Concrete[J],Journal of Advanced Concrete Technology,2003,(1):5-15
[2]T.L.萨蒂著,许树柏等译.层次分析法—在资源分配、管理和冲突分析中的应用[M].北京:煤炭工业出版社,1988
[3]王莲芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990
[4]赵焕臣,许树柏,和金生编著,刘豹审订.层次分析法—一种简易的新决策方法[M].北京:科学出版社,1986
[5]秦寿康等著.综分评价原理与应用[M].北京:电子工业出版社,2003
[6]刘华良,石建军,宁严庆.自密实混凝土测试方法与技术研究[J].混凝土,2008,(03):90-93

