基于流量负载的改进型几何抽样算法
孙 昱,夏靖波,赵小欢,申 健
(空军工程大学 信息与导航学院,陕西 西安710077)
网络流量测量和分析是研究网络行为的基础,其对于网络问题的解决、协议的调试和网络性能评估等方面均有极大的帮助。但是随着近年来高速网络技术的发展,想要全部采集链路上的数据流量十分困难,而且需要巨大的开销,因而抽样测量技术成为当今在高速链路上进行流量测量的一种解决方案。近年来,对网络流量抽样技术的研究已成为高速网络流量测量研究的重点内容。
1993年,Claffy在测量NSFNET主干网流量时,对采用不同触发机制的传统抽样方法进行了分析对比[1],证明了基于计数触发机制的抽样算法要普遍优于基于时间触发机制抽样算法。2005年,Duffield等人指出了均匀抽样在流量测量领域存在的问题,并提出了“非均匀抽样”的方法[2]。由于自适应抽样可以利用网络流量的相关性预测流量状态,并实时调整抽样策略或参数以获得更好的测量效果,因此逐渐受到重视。自适应抽样算法主要分为两类,一类通过流量模型对未来的流量进行预测,然后根据预测的结果动态地调节抽样概率以提高测量的精度,目前应用效果比较好的模型是FARIMA模型[3-4]和NMSM模型[5]。另一类自适应算法主要从抽样资源有限的角度出发,通过调节抽样概率匹配报文的到达速率以避免资源耗尽对测量造成的不利影响。抽样资源主要包括设备的处理能力和缓存等,目前,这方面的大多数研究工作都是根据缓存容量的大小来设计自适应的抽样方案[6-8]。但是由于网络流量具有突发性,在流量高峰期短时间内来的报文基数会很大,采用基于缓存的自适应抽样也同样难以避免缓存溢出而导致的报文丢失,进而影响了抽样算法的效能,使得测量不能准确地反映峰值的状况。要较好地解决这一问题,还必须将抽样设备的处理能力考虑在内,由于几何抽样具有良好的抽样性能,因此,本文将对其进行改进,使之能根据抽样设备的处理能力和流量负载动态地调节抽样概率,通过降低设备的丢包率来提高网络流量的测量精度。
1 算法分析
几何抽样算法[9]是以固定的概率p对经过的每个报文进行抽样,当每到达一个报文时,网络节点就产生一个在0~1之间服从均匀分布的伪随机数,若该随机数小于抽样概率p,则该报文被抽中,否则该报文被丢弃。它的抽样间隔X服从概率为p的几何分布,即P(X=n)=(1-p)n-1p。几何抽样是一种运用广泛的抽样技术,与RFC2330所推荐的泊松抽样一样,具有以下优点:1)样本在总体中分布均匀,分析所得的各种参数都相对比较准确;2)不易引起同步效应,能够用来准确地收集周期行为的测量样本;3)抽样方法实现简单,具备良好的可扩展性。
当一个报文被抽中时,网络节点将对其进行分析以得到某些需要的信息,然后将这些信息存入存储设备中,这段时间称为报文的处理时间。在网络流量的高峰时期,报文的到达速率将高于网络节点对报文的处理速率。因此,当节点正在处理某个抽中报文时,很可能有新的报文到达并被抽中,此时,新抽中的报文将被存放于网络节点的缓存中等待处理。但是在流量高峰期短时间内经过节点的报文基数很大,节点抽中的报文数量相对较多,来不及处理的报文都被放入缓存中,将很快造成缓存溢出,导致丢包率过高。虽然可以从硬件的角度,例如通过增加缓存容量和改善缓存结构[10]等方法来缓解这一问题,但是这些措施的扩展能力不强而且所需的成本太高,因此应用受到限制。
报文被丢弃会对测量的精度造成十分不利的影响,以网络流量的测量为例进行说明。当测量单位时间内网络中经过的流量时,通过采样得到单位时间内的一个样本X1,X2,…,Xn,Xi表示第i个抽样报文的字节数。那么该段时间内经过链路总流量的估计值为由于一些被抽中的报文还来不及处理就被丢弃了,这将导致:1)抽样样本的随机性变差,这会直接影响测量结果的精度;2)估计量X*是无偏估计的前提条件是样本由等概率抽样获得,而发生报文丢弃的事件将破坏这一前提条件,也会造成测量精度的下降。
2 改进方案
报文被丢弃的根本原因是在流量高峰时网络节点的处理能力与报文的到达速率不匹配,造成抽样报文在缓存中累积,当达到缓存容量的上限时被丢失。节点工作最理想的状态是当节点处理完上一个抽中报文时恰好抽中下一个报文,这样每一个抽中的报文将得到及时的处理而不会在缓冲中累积,丢失的报文数将大大减小。为了实现这一点,抽样算法应该根据流量负载的动态变化自适应地调节抽样概率以匹配节点的处理能力从而尽量避免报文的丢失。
2.1 抽样概率的调节
报文的到达过程如图1所示。
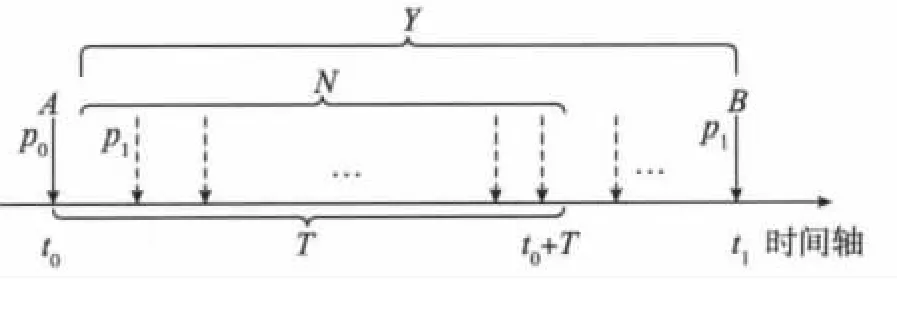
图1 报文的到达过程
图1 中垂直的箭头代表报文的到达,实线的箭头代表该报文被抽中,虚线代表该报文未被抽中。假设节点处理一个报文需要的平均时间为T,若该节点在时刻t0时以概率p0抽中了一个报文A,然后再有报文到达时,节点将以新的抽样概率p1进行几何抽样,直到在时刻t1抽中下一个报文B。在时段(t0,t0+T]内,经过节点的报文数为N,在时段(t0,t1]内,经过节点的报文数为Y。当t1≤t0+T时,由于节点正在处理报文A,若不考虑节点的缓存,报文B因来不及处理而被丢弃;当t1>t0+T时,报文A已被处理完,节点能接着处理报文B。由于Y是服从几何分布的随机变量,有P(Y=n)=(1-p1)n-1p1,因此报文B不被丢弃的概率为

若报文B不被丢弃的概率大于α,根据式(1),即(1-p1)N≥α,由此得出下一步的采样概率p1满足

但是节点在抽中A后计算下一步的抽样概率p1时,并不知道N的取值,此时节点只能依据历史信息对N进行估计。在时段(t0,t0+T]内,报文到达的平均间隔Δt近似为T/N,在前一个相似的抽样时段(t0',t0]内,报文到达的平均间隔Δt'≈(t0-t0')/Y'。流量高峰时,时段(t0',t0+T]极短,可以认为该段时间内报文的到达是均匀的,即Δt=Δt'。由此得到

由于在前一个时段(t0',t0]中,进行几何抽样的概率是p0,所以,E(Y')=1/p0,故
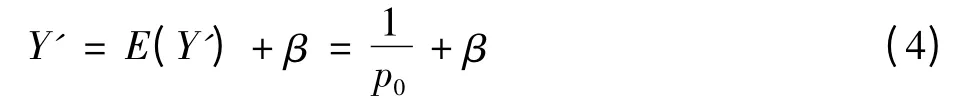
式中:β为修正值。联立(3)和(4)可得

将式(5)带入式(2)中,得到下一步的抽样概率为
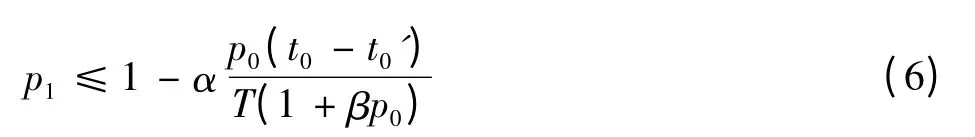
在流量高峰时,抽样算法将根据节点的处理能力和负载状况利用式(6)动态计算抽样概率以减少丢弃的报文数量。
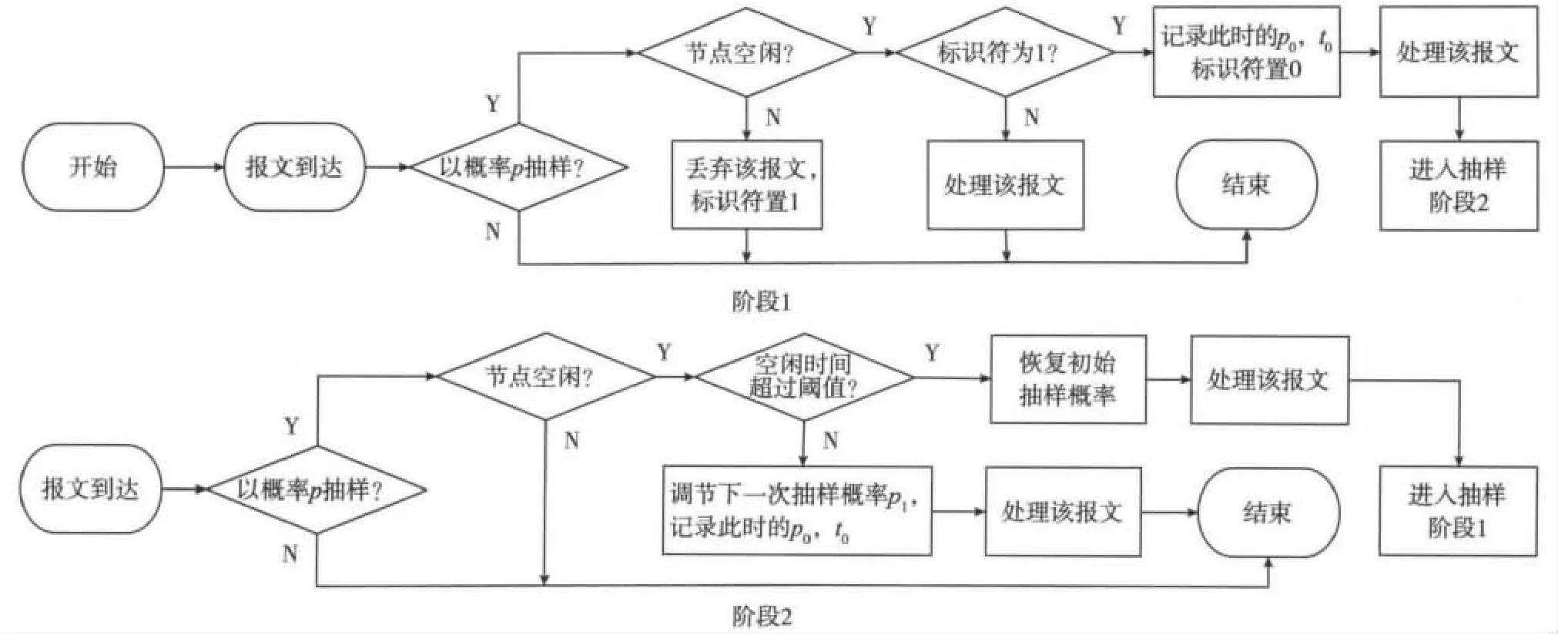
图2 改进型算法的基本流程
2.2 算法流程
改进型几何抽样算法的基本流程如图2所示。
当有报文到达时,节点将以抽样概率p对该报文进行抽样,初始的抽样概率为给定值p'。如果该报文被抽中,则判断网络节点此时是否空闲,如果节点正忙导致该报文被丢弃,则很有可能发生了流量负载过重的情况,此时将标识符置1。当下一次抽中报文且节点空闲时,由于标识符为1,那么算法在记录式(6)需要用到的相关参数后将进入自适应的抽样阶段2。在阶段2中,每次抽中报文且节点的空闲时间没有超过阈值时,都会利用式(6)动态地调整下一次的抽样概率p。如果节点的空闲时间超过了阈值,即可认为流量负载减轻了,此时,恢复初始的抽样概率p'并进入阶段1中进行抽样。
由于改进型几何抽样算法的采样概率p是可变的,得到的样本是一个非均匀采样的样本,因此在对结果进行估计时无法使用基于等概率采样的估计量。而Horvitz-Thompson估计量一个适用于非均匀采样的无偏估计量[11],因此可以使用它来估计总体的特征参数。例如在测量网络流量时,得到抽样样本X1,X2,…,Xn后,先使用Horvitz-Thompson估计量估算无偏的总体均值,然后估计单位时间内经过节点的总流量为X*=NˉX=N×
3 实验验证
本文实验所用数据来自MAWI工作组[12]在互联网骨干链路上全流量采集中随机抽取的100 s流量数据。该流量数据中报文到达的平均时间间隔为606.3μs,假定网络节点处理一个报文需要的时间T为200μs。几何抽样的抽样概率为p=0.8,改进型几何抽样的初始抽样概率为p'=0.8,流量高峰时报文不丢弃的概率α=90%。
3.1 有效性分析
为了衡量抽样算法的有效性,首先定义两个评价指标。第一个为单位时间内丢弃的抽中报文的数量,该指标能直观地反映算法对流量负载的适应能力。由于改进型几何抽样算法会在流量高峰时降低抽样率,因此若其丢包数量更低并不足以说明该算法有效,故定义第二个评价指标丢包率为单位时间内丢弃的报文个数与抽中的报文总数之比。利用MATLAB进行仿真,结果如图3和图4所示。

图3 单位时间丢弃的报文数比较

图4 单位时间的丢包率比较
从图3中可以看出,改进型几何抽样算法丢包数量明显低于原抽样算法,其单位时间内平均丢包数为101.07个,标准差为27.35,而原算法单位时间内平均丢包数为297.48个,标准差为79.70,这说明,改进后的算法能有效降低节点丢弃的报文数量。流量高峰时,改进算法的理论丢包率为10%,但是由于在非流量高峰时也有可能发生丢包的情况,因此实际丢包率将略高于10%。图4中,改进型算法的平均丢包率为15.67%,标准差为1.99%,原算法平均丢包率为22.50%,标准差为1.83%。从图4中还能看出,改进型算法在任一时段的丢包率均低于原算法,如果实际网络流量突发次数多且持续时间较长,那么二者的差距将十分明显。由于改进算法丢弃的报文个数和丢包率均更低,证明了该算法对流量负载的变化具有更好的适应性。
3.2 测量精度比较
利用上述算法得到的样本分析单位时间内经过节点的网络流量,定义测量误差,其中,为估计流量,Q为实际流量,分析结果如图5所示。

图5 测量误差比较
改进型几何抽样的平均测量误差为7.20%,标准差为5.33%,而改进前的平均测量误差为49.14%,标准差为4.66%。这说明改进后的算法得到的样本容量虽然可能减少,但是其样本的随机性却明显更优,从而使测量的参数更精确,同时也证明了减少网络节点丢弃的报文数确实能在很大程度上提高网络测量的精度。由于在仿真时并没有考虑节点的缓存,而实际的抽样设备均有一定容量的缓存,所以该算法在实际应用时,所得的相对误差还将进一步降低。
如果实验所用的流量数据在时间上是均匀分布的,即每隔606.3μs到达一个报文,那么抽样算法即使以概率p=p0=1抽样,节点也能顺利地处理完所有报文而不存在测量误差。但是根据测量结果可知网络流量的突发是不可预测的,在任意测量时间内都可能出现流量突发的情况,因此所做的改进是十分必要的。
4 小结
随着高速网络的不断发展,网络测量的应用变得越来越普遍。本文提出的改进型几何抽样算法能根据流量负载的变化自适应调节抽样概率以匹配网络节点的处理能力,从而较好地解决流量突发时丢包率过高造成测量结果不精确的问题。该算法实现简单,可扩展性强,能为其他抽样技术的应用起到一定的借鉴作用,本文的下一步工作是考虑抽样设备的实际缓存来将该算法进行具体的应用。
[1]CLAFFY K C,POLYZOS G C,BRAUN H W.Application of sampling methodologies to network traffic characterization[J].SIGCOMM Computer Communication Review,1993,23(4):194-203.
[2]DUFFIELD NG,LUND C,THORUP M,et al.Sample less:control of volume and variance in network measurement[J].IEEE Trans.Information Theory,2005,51(5):1756-1775.
[3]HARMANTZIS F C,HATZINAKOS D.Heavy network traffic modeling and simulation using stable FARIMA processes[EB/OL].[2012-10-10].http://www.stevens-tech.edu/perfectnet/publications/Papers/H H_ITC19.pdf.
[4]潘乔,罗辛,王高丽,等.基于FARIMA模型的流量抽样测量方法[J].计算机工程,2010,36(15):7-11.
[5]陈松,王珊,周明天.基于实时分析的网络测量抽样统计模型[J].电子学报,2010,38(5):1177-1180.
[6]王洪波,韦安明,林宇,等.流测量中基于测量缓冲区的时间分层分组抽样[J].电子学报,2006,17(8):1775-1784.
[7]张震,汪斌强,朱珂.流量测量的关键技术分析与研究[J].计算机应用研究,2009,26(9):3442-3447.
[8]陈庶樵,张果,朱柯.一种基于包速率自适应的报文抽样算法[J].计算机应用研究,2010,27(7):2727-2729.
[9]杨家海,吴建平,安常青.互联网络测量理论与应用[M].北京:人民邮电出版社,2009.
[10]张进,刘勤让,司亮,等.一种基于两级存储结构的网络流量测量算法[J].计算机工程,2007,33(10):10-12.
[11]HORVITZ D G,THOMPSON D J.A generalization of sampling without replacement from a finite universe[J].Journal of the American Statistical Association,1952,47(26):663-685.
[12]MAWI working group traffic archive[EB/OL].[2012-02-02].http://mawi.wide.ad.jp/mawi.

