真随机数在数字图像加密中的应用

王吉宇，吴 飞，杜永贵，李艳萍

(太原理工大学 信息工程学院，山西 太原030024)

随着信息技术和网络技术的发展，数字图像在信息安全领域得到广泛应用，它的安全性随着应用的普及越来越重要。比如，必须保护军事分布图、间谍卫星拍摄的重要照片、商业机密图片等，涉及领域大至国家安全，小至企业和个人信息安全，数字图像的安全已成为信息安全领域中的研究焦点。近些年发展迅猛的技术有:图像加密、图像隐藏、图像伪装等，其中数字图像加密技术不仅可以有效地保护要传输图像的信息，而且还可作为其他技术的预处理和后处理等［1］。因此，对图像加密技术的深入研究具有非常重要的现实意义。

近年来，国内外的研究学者提出了多种加密方法:Schwartz给出了基于伪随机序列的加密技术［2］;国内解鲲等人提出了一种基于m序列的图像随机加密与实时传输方案［3］;还有基于混沌系统的数字图像加密算法［4］、基于“密钥图像”的加密技术等［5］，最近提出的图像置乱技术也是一种不容忽视的有效加密方法。这些方法在一定程度上满足了图像加密的需求，但加密的密钥或序列不是真随机的，不具有严格的独立性和完全的可靠性，因此更高效、更安全的加密算法有待进一步研究和探讨。

基于真随机数生成器产生具有独立性、均匀分布性的真随机序列，提出了利用真随机数对数字图像像素序列进行异或的加密算法，加密前对原始图像进行Arnold变换的图像置乱，在接收方进行异或解密、Arnold变换周期还原获得原始图像，加密过程简单，图像置乱提高了保密性。重点研究真随机数生成器的设计和实现，对图像置乱进行简要说明。经实验证明，加密后图像的像素相关性小，具有良好的抗剪切攻击和抗噪声性能。

1 数字图像加密过程

数字图像是由模拟图像数字化得到的，通常以二维数字组(行和列)形式表示，基本元素为像素，可以用计算机或数字电路来存储和处理［6］。像素是在模拟图像数字化时对连续空间进行离散化得到的，每个像素具有整数行和列位置坐标，同时具有整数灰度值或颜色值，常见的有灰度图像和彩色图像。灰度图像中每个像素可以由0(黑)～255(白)的亮度值表示，0～255之间表示不同的灰度级，每幅彩色图像是由红绿蓝3幅不同颜色的灰度图像组合而成，因此数字图像加密本质上是对灰度图像进行的加密，即对灰色图像的像素位置坐标或灰度值的加密。

用真随机数对灰色图像进行加密的过程如图1所示，首先对原始灰色图像进行基于Arnold 变换的分块图像置乱，改变像素点的位置;然后将置乱图像像素点的8 bit灰度值序列与真随机序列相异或，改变原先像素点的灰度值，得到最终的加密图像。真随机序列由真随机数生成器产生，随机统计特性满足由美国国家标准与技术研究院(National Institute of Standards and Technology，NIST)指定的随机数统计特性测试标准［7］，具有严格的独立性和完全的可靠性，与灰度值序列异或后的序列同样具有真随机的特性，因此加密图像具有很高的保密性。

图1 数字图像加密和传输过程

1.1 图像置乱

在Arnold变换基础上提出一种分块图像置乱算法［8］，如图2所示。先对原始图像进行分块操作，再进行图像块和块内像素点的Arnold变换置乱，获得置乱图像，该算法迭代次数少、置乱速度快、执行效率高。Arnold变换具有周期性［9-10］，即当迭代次数达到一定值L后，图像的所有像素点又都回到初始位置，置换图像恢复为原始图像，这个最小定值L被称为置乱周期L。当发送方将置乱次数为m(m＜L)的图像传输到接收方时，接收方再作L-m次置乱即可得到原始图像。可利用这一特性将置乱图像还原为原始图像。

图2 分块图像置乱算法

在数字图像的发送方，将一幅大小为N×N(N＞64)的图像划分成若干个大小为n×n的图像块，得到个图像块，对图像块和块内像素点都进行Arnold变换置乱，打乱图像块的排列顺序和块内像素点的位置，完成了整幅图像的置乱。二维Arnold变换公式可表示为

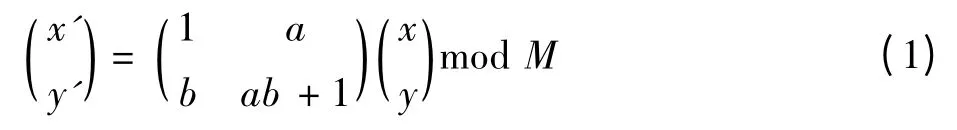
当a=1，b=1时，得到标准的Arnold变换公式

在数字图像的接收方，仍然可依据Arnold变换的周期性将分块的置乱图像还原为原始图像，假设图像块的Arnold变换置乱周期为L1，图像块内像素点的Arnold变换置乱周期为L2，发送方对图像块进行S1次Arnold变换，对图像块内像素点进行S2次Arnold变换，接收方只需要再对图像块作L1-S1次Arnold变换，对图像块内像素点作L2-S2次Arnold变换，即可恢复出整幅图像。

1.2 真随机数的产生

用纯数字电路的方式实现了真随机数生成器(TRNG)的设计，其核心思想是利用查找表(LUT)的方法设计RS触发器，利用其亚稳态作为随机源，多组触发器的输出经过异或和同步处理后得到随机序列，PC机通过串口输出模块采集真随机序列，该TRNG在XC3S400物理平台上实现并进行测试验证。

如图3所示，RS触发器的R、S端连接时钟信号CLK，当CLK=0时，触发器的稳定输出为(Q)=(1，1);当CLK=1时，经历决断时间后输出稳定在(Q)=(1，0)or(0，1)。更精确一些，在CLK上升沿到来时，触发器进入亚稳态，经过决断时间输出Q最终稳定在0或1，输出量Q具有随机性，这就为随机数的产生提供了熵源。

图3 基于RS触发器的随机数发生器

查找表(LUT)结构本质上是1个RAM，它类似于1块有4个输入、16个输出的16位的存储器。这个存储器里面存储了所有可能的结果，然后由输入来选择哪个结果应该输出。用户通过原理图或者HDL语言来描述1个逻辑电路时，FPGA的综合软件和布局布线软件会自动计算逻辑电路中所有可能的结果，并且把结果事先写入RAM［11］。这样对输入信号进行逻辑运算就相当于输入1个地址进行查表，找出并输出地址对应的内容。即可利用LUT实现FPGA器件的逻辑功能。

因此可以用基于查找表的原理实现RS触发器的逻辑功能。如图4所示，编制两个可配置逻辑模块(CLB)即可实现RS触发器的逻辑功能，RS触发器的2个与非门可由Slice中的LUT设计完成，把Slice1和Slice2的位置约束在左右相邻的2个CLB中，并在前后加入2个内嵌的D触发器元件，分别称为触发器A和触发器B。触发器A能减小输入时钟CLK的相位偏移，触发器B能解耦Q端的容性负载，提高输出序列的随机性。把基于LUT设计完成的RS触发器称之为LUT触发器。

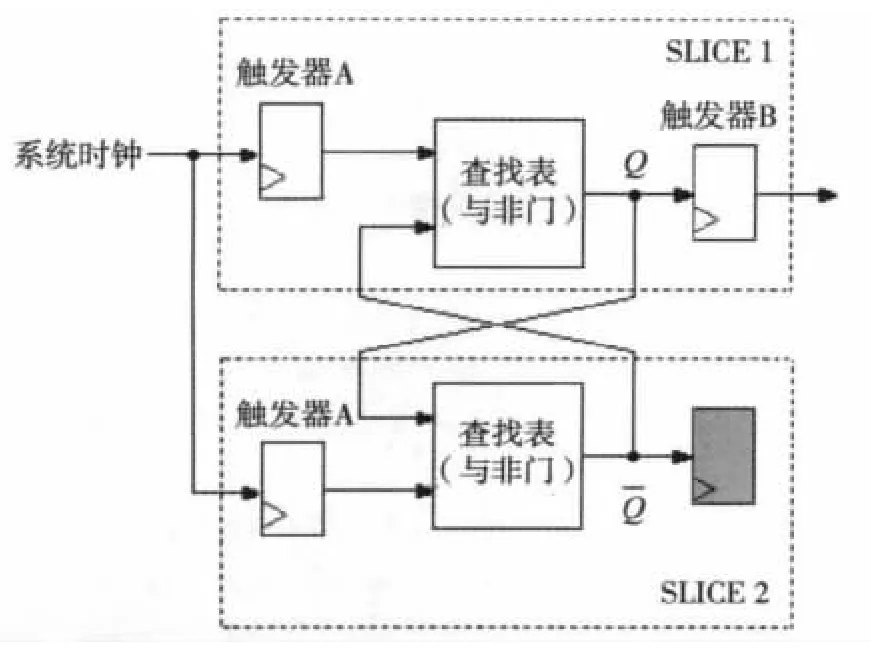
图4 LUT触发器(内含查找表和嵌入式触发器的RS锁存器)

对多个同步的LUT触发器的输出进行异或操作，可降低序列的相关性，使得产生的序列具有良好的随机性。设计的随机源模块如图5所示，对256个LUT触发器的输出进行异或。最后由2个D触发器以1个较低的时钟频率进行采样和同步，从而得到真随机序列。

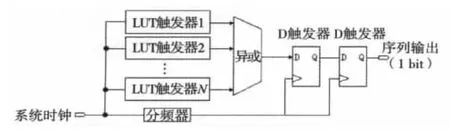
图5 随机源模块的设计

该TRNG在XC3S400物理平台上实现并进行了测试验证，系统时钟频率为100 MHz，PC机通过串口输出模块采集到速率为12.5 MHz的真随机序列，其随机统计特性满足NIST指定的随机数统计特性测试标准，NIST测试结果如表1所示，15项指标测试均通过，说明产生的真随机数具有良好的随机性和可靠性。

2 实验结果与分析

为验证基于Arnold变换的分块图像置乱算法、真随机数加密的有效性和安全性，对其进行仿真实验，实验结果如图6所示，将加密后的图像再次与同一组真随机数进行异或，然后经过Arnold周期置乱可以还原为原始图像。恢复后的图像同原始图像无明显差异，说明真随机数对置乱后的图像有很好的加密和解密作用，能应用于数字图像的加密中。

原始图像先经过分块置乱，打乱像素点的位置，得到初步的安全加密;再经过真随机数异或加密，使得攻击者恢复原图像，窃取图像信息的概率大大降低。

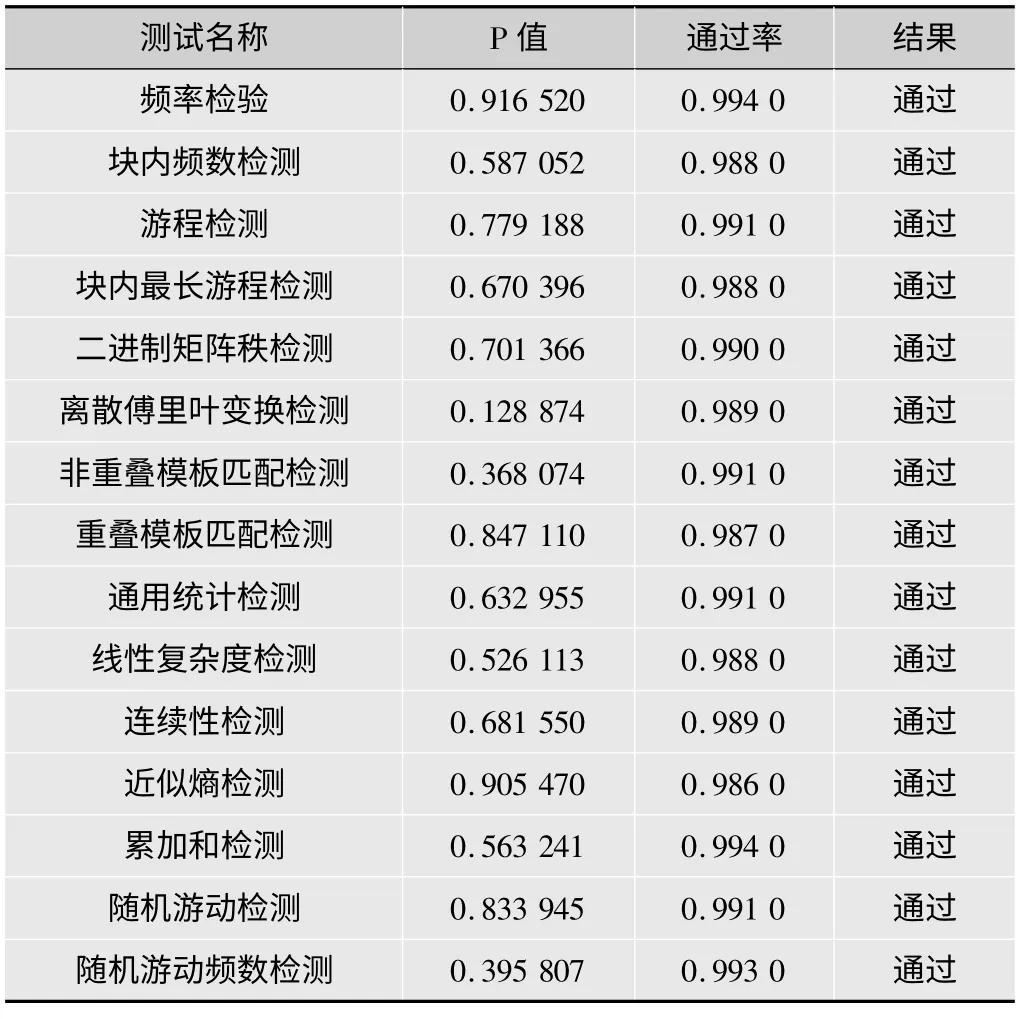
表1 随机序列的NIST测试结果(256组LUT触发器)

图6 图像分块置乱、加密、恢复的结果图

下面对该加密过程的抗攻击性能进行分析，检验该加密过程能否有效地阻止攻击者对图像的破坏，主要从抗剪切及抗噪声等方面进行分析，实验结果如图7～图9所示。

图7 抗剪切能力分析

从图7可以看出加密图像在遭到剪切攻击后，能较好地恢复原始图像，且信息保存完整;从图8、图9可以看出加密图像加入各种噪声后恢复出的图像都比较清晰。以上结果说明该加密过程具有良好的抗剪切攻击和抗噪声性能。

3 结论

本文提出了利用真随机数对数字图像像素序列进行异或的加密算法。加密前对原始图像进行基于Arnold变换的图像分块置乱，在接收方进行异或解密、Arnold变换周期还原获得原始图像，加密过程简单，图像置乱提高了保密性。经实验证明，加密后图像的像素相关性小，具有良好的抗剪切攻击和抗噪声性能。

［1］钟文琦，刘雪，商艳红，等.一种改进DES的数字图像加密方法［J］.北方工业大学学报，2005，17(1):10-14.

［2］SCHWARTZ C.A new graphical method for encryption of computer data［J］.Cryptologia，1991，15(1):43-46.

［3］解鲲，乌旭.一种基于m序列的图像随机加密与实时传输方案［J］.现代电子技术，2003，151(8):22-25.

［4］罗军.基于混沌系统的数字图像加密算法［J］.计算机工程与设计，2009，30(8 ):1844-1845.

［5］KUO C J.Novel image encryption technique and its application in progressive transmission［J］.J.Electron，Imaging，1993，2(4):345-351.

［6］数字图像［EB/OL］.［2012-08-09］.http://baike.baidu.com/view/286845.htm.

［7］RUKHIN A，SOTO J，NECHVATAL J，et al.A statistical test suite for random and pseudorandom number generators for cryptographic applications［R］.U.S.Department of Commerce:NIST Special Publication，2010.

［8］王圆妹，李涛.基于Arnold变换的高效率分块图像置乱算法的研究［J］.电视技术，2012，36(3):17-19.

［9］KWOK H S，TANG W K S.A fast image encryption system based on chaotic maps with finite precision represention［J］.Chaos，Solitons & Fractals，2007，32(4):1518-1529.

［10］郭利文，邓月明.CPLD/FPGA设计与应用高级教程［M］.北京:北京航空航天大学出版社，2011.

［11］NIST.Statistical test suite［EB/OL］.［2012-08-18］.http://csrc.nist.gov/groups/ST/toolkit/rng/documentation_software.html.