一种激光三角测厚中非线性的校正方法＊

汪 琛，赵 斌

（华中科技大学 机械科学与工程学院，湖北 武汉 430074）

引 言

激光三角法是常用的位移测量方法，利用双光路激光三角法进行厚度测量是一种广泛应用的在线测厚方式，其特点是健康环保，实时性好，测量速度快，标定简单，操作方便，不足之处是被测物振动对其测量精度影响较大［1－4］。单镜头激光三角法是一种高精度、测量不受被测物振动影响的在线测厚方法，其测厚原理基于直射型激光三角法和理想光学系统成像原理，在C型测量臂的量程范围内，放置任意一块非透明物体，均可准确得到被测物厚度。

单镜头激光三角法测厚仪的精度取决于以下几个方面：（1）光学及机械零部件的加工精度；（2）作为光源的上下激光器是否同轴对准以及其它零部件定位的准确性；（3）光学系统像差的大小和光斑成像质量；（4）激光器和图像探测器在检测工作中的稳定性；（5）环境影响因素的减小或消除［5－6］。要获得更高的测量精度，除了控制前述精度影响因素外，还需在标定时减小原理误差。

1 单镜头激光测厚仪分析

1.1 测厚原理

仪器外观如图1所示，测厚仪固定在具有等间距安装孔和水平调节机构的支撑架上，测厚仪的姿态由调节机构来控制。被测物置于升降调节架上，通过高度调整使被测物位于测厚仪量程范围内。设备的光学系统固定在侧板上，金属罩壳起遮挡杂散光和减少粉尘、水汽进入设备内的作用。图形探测器上检测到的信号通过USB数据线传输至图像处理设备，用来精确计算被测物厚度。

图1 激光测厚仪测量方式示意图Fig.1 The schematic diagram of measurement mode

图2为系统测厚原理示意图，上下激光器发出的平行光束经透镜聚焦到被测物上下表面，漫反射光线经过孔径光阑、平面玻璃片后由成像透镜分别汇聚到图像探测器上。图3为其光学模型示意图，经过透镜光轴且垂直于激光器光束轴心线的平面设定为参考平面，则被测物上下表面的光斑可分别视为相对于参考平面高度为Δh1和Δh2的两个物体，在成像透镜后方所成像的像高分别为h1和h2。由几何光学可知，光学系统近轴区可视为理想光学系统，在近轴区内，垂轴放大率β定义为像的大小与物体的大小之比［7］，因而在图3中有：

由式（1）可知：h1＝βΔh1，h2＝βΔh2，于是有：

式中，（Δh1＋Δh2）为被测物的实际厚度，（h1＋h2）为图像探测器上两光斑的间距，这样求被测物的厚度值即转化为计算光斑间距值。

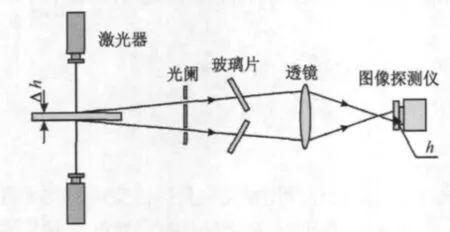
图2 单镜头激光三角法原理图Fig.2 The schematic diagram of single lens laser triangulation

图3 光学模型示意图Fig.3 The schematic diagram of optical mode

安装和测量时，上下激光器要求同轴对准且相对于被测物上下对称，以减小因物面倾斜时上下光斑相互错移造成的测量误差。被测物位于上下激光器镜头的焦平面处，此时被测物上下表面处光斑直径最小，重心法定中心精度也越高。孔径光阑位于平面玻璃片前方且距离透镜中心一定距离，其孔径角和通光孔直径用于限制入射光线的角度和通光量。平面玻璃片位于孔径光阑和成像透镜之间，呈一定倾角放置，其像移特性会使图像探测器上的光斑相对远离。图像探测器位于成像透镜后方，用于接收透镜汇聚的光线。

1.2 系统标定

为了确定光斑间距与被测物厚度的函数关系式，对系统进行实验标定。选用的激光器功率为1mW，发出的激光波长为635nm，光束发散度0.5mrad，椭圆率1∶1.4。图像探测器选用分辨率为2 048×1 536的CMOS相机，像元尺寸3.2μm×3.2μm。共选用0.03，0.04，0.05，0.06，0.07，0.08，0.09，0.10，0.15，0.20，0.25，0.30，0.40，0.50，0.75，1.00，1.50，2.00，2.50，3.00（单位：mm）共20组已知厚度被测物进行标定实验。通过图像处理得到各组厚度对应的光斑间距值，以像素个数为单位，并利用最小二乘拟合得到不同厚度时光斑间距与被测物厚度真值之间的函数关系式。

测量系统中，对于同一个被测物，其在C型测量臂的位置可在量程范围内任意选定，如图4所示，1和5大致代表上极限测量位置和下极限测量位置，超出此范围时，被测物上下表面的两个光斑将无法同时成像于图像探测器上。进行标定实验时，先将测厚仪支撑架和升降调节架上的托架大致调水平，然后依次选取1号到5号测量位置之间的基本等分的若干点进行测量，并取这些测量位置处光斑间距值的平均值进行数据标定。

图4 测量位置示意图Fig.4 The schematic diagram of measurement site

图5 测量厚度—光斑间距拟合曲线Fig.5 The fitted curve of measured thickness－facula space

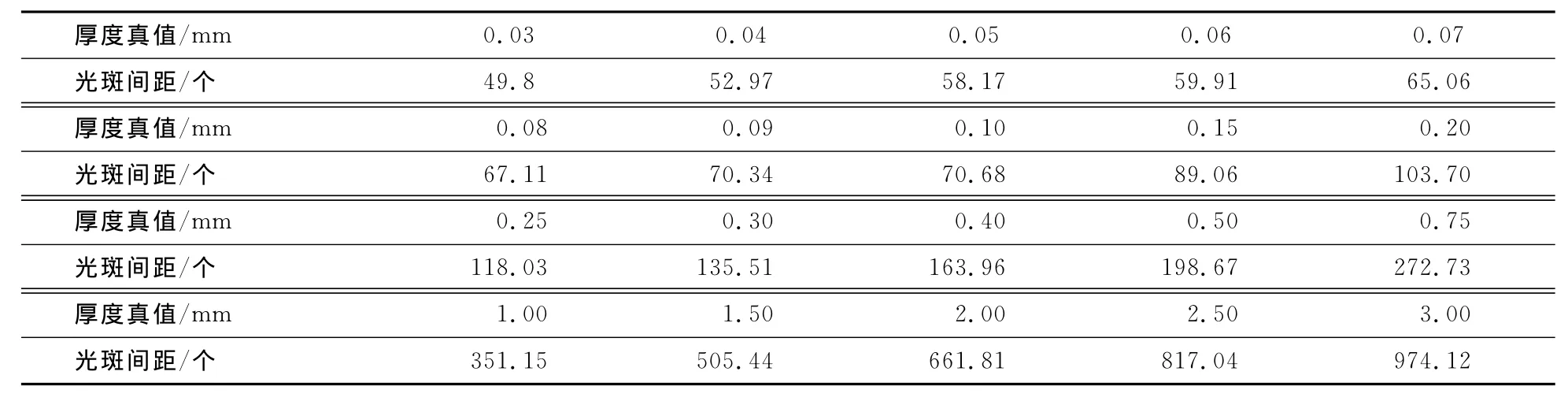
表1 标定实验数据Tab.1 The data of calibration experiment

表1列出了不同厚度被测物厚度真值及其对应的光斑间距的平均值，通过最小二乘拟合得到标定函数式：

式中，Δh为测量厚度，h为图像探测器上两光斑间距值。由此标定函数式计算20组被测物测量厚度并绘制测量厚度－光斑间距平均值的拟合曲线，得到表2和图5：

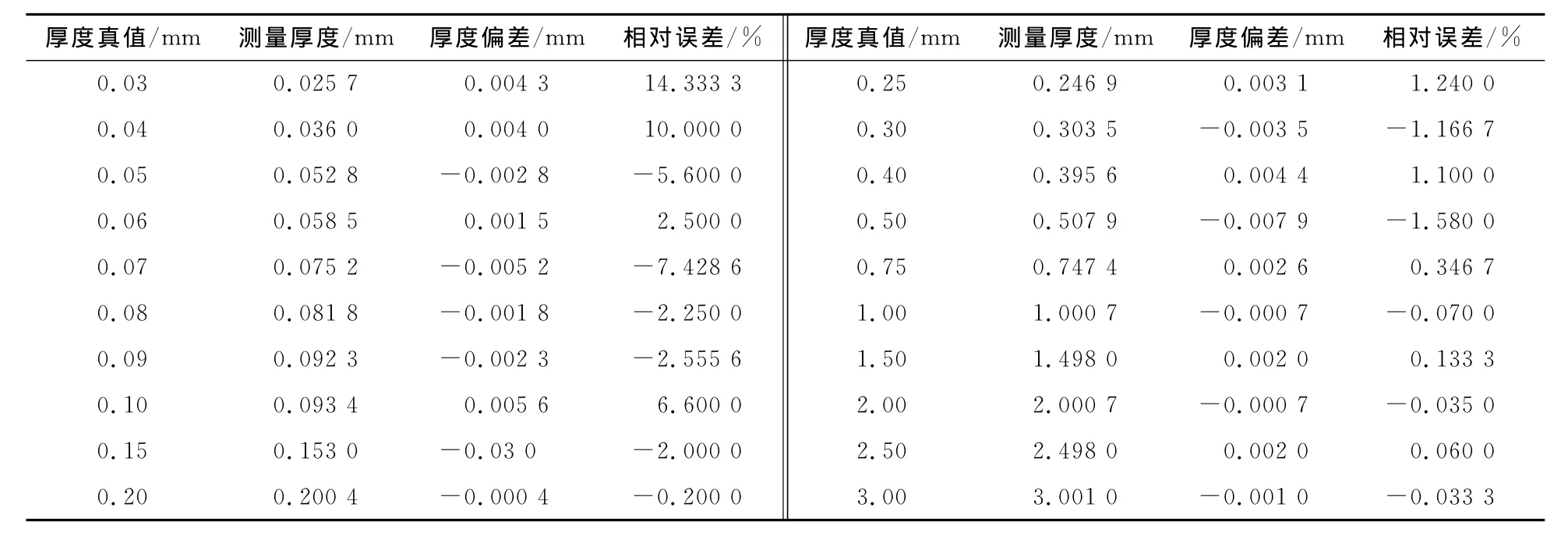
表2 校正前精度分析数据Tab.2 The data of precision analysis before calibration

从表2中可以看出，标定后系统在0.05～3mm范围内系统误差普遍在0.003mm左右，最大误差为0.007 9mm，最大相对误差为－7.4%，误差较小，并且从图5中可以看出，其线性度较好，证明用光斑间距和被测物厚度真值数据拟合标定方程的方式精度较高。在上述标定中，同一厚度不同位置的光斑间距值只作了平均处理。接下来取0.05mm，0.1mm，0.5mm，1mm，2mm，3mm六组被测物的测量数据，绘制其测量厚度—测量位置拟合曲线来分析不同测量位置时测量厚度与光斑间距的关系。

从图6中可以看出，被测物位于不同位置时，厚度波动变化明显，剔除粗大误差点后最大波动量大约在20μm左右，即两光斑间距值会随着被测物位置的不同而明显变化，且两者关系是非线性的，此非线性因素会对系统精度造成一定影响，需要进行非线性校正。

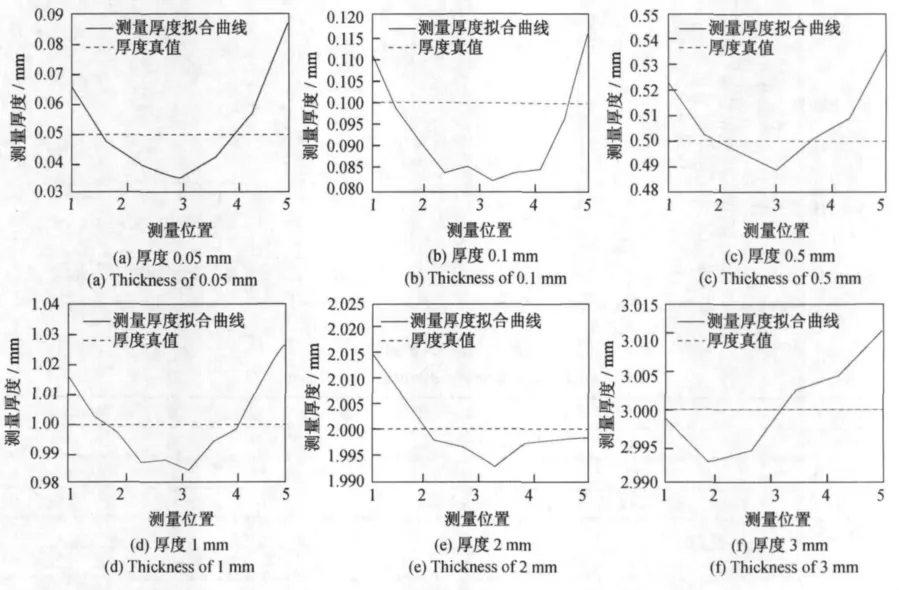
图6 测量厚度—测量位置拟合曲线Fig.6 The fitted curve of measured thickness vs.measured site

2 非线性校正

2.1 校正方法

影响光学成像系统质量的因素主要有以下几点：实际的光学零件加工精度很难保证透镜球面面形的精确性，光学材料自身的不均匀性导致折射率在透镜不同地方不为恒定值，另外零件的定位精度也难以达到光学系统设计要求，同时电压波动会引起激光器发光不稳，造成激光光斑中心的飘移，还有图像探测器像元的奇偶不均匀性等等［8］。这些因素共同作用下会造成标定时，同一被测物在图像探测器上的两个成像光斑间距会随着被测物位置的变化呈现非线性变化，要获得更高测量精度就需要对此非线性进行校正。

针对光斑在图像探测器上的坐标位置随着被测物测量位置变化的非线性关系，可在图像探测器坐标上，分别拟合单个光斑随被测物位置变化的函数关系式，再由两者的差值得到两光斑的间距，来减小光斑间距随测量位置不同的变化程度，进而减小被测物位置不同而造成的测量数据波动程度。

被测物位于不同测量位置时，其上下表面看作相对参考平面高度为Δh1和Δh2的两个平面，此时，图像探测器上的成像光斑在探测器的坐标轴上横坐标分别为x1和x2，采用三阶函数进行数据拟合。

被测物上表面高度Δh1和图像探测器上成像光斑横坐标x1的关系式为：

被测物下表面高度Δh2和图像探测器上成像光斑横坐标x2的关系式为：

被测物厚度为H＝Δh1－Δh2，整理得：

方程右边共有7个未知数，用若干组厚度为Hi的被测物在j个测量位置对测量系统进行标定，可得到上下光斑的i×j个方程：

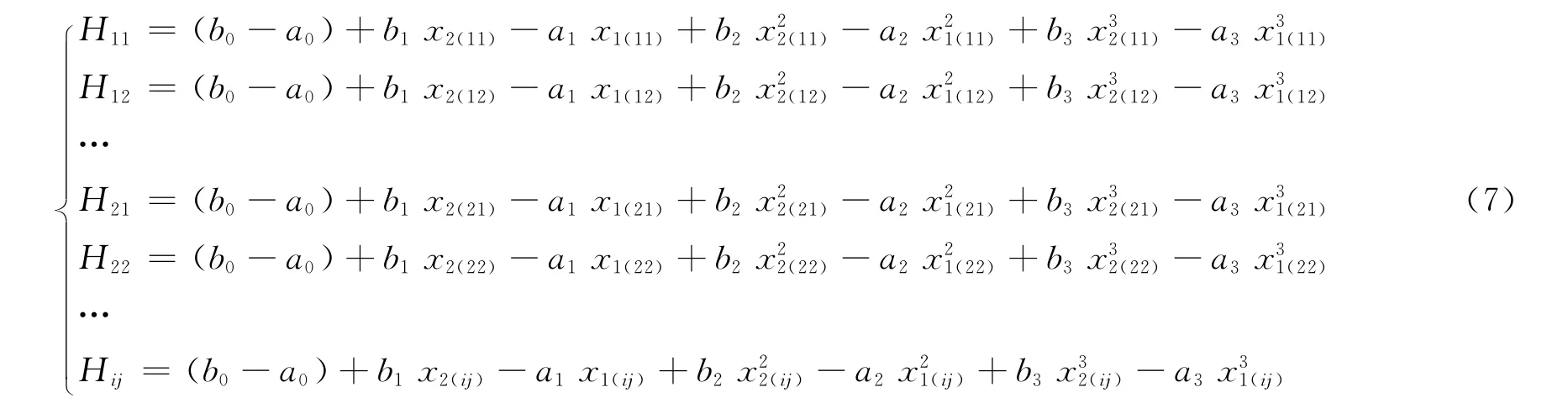
变换为矩阵形式：

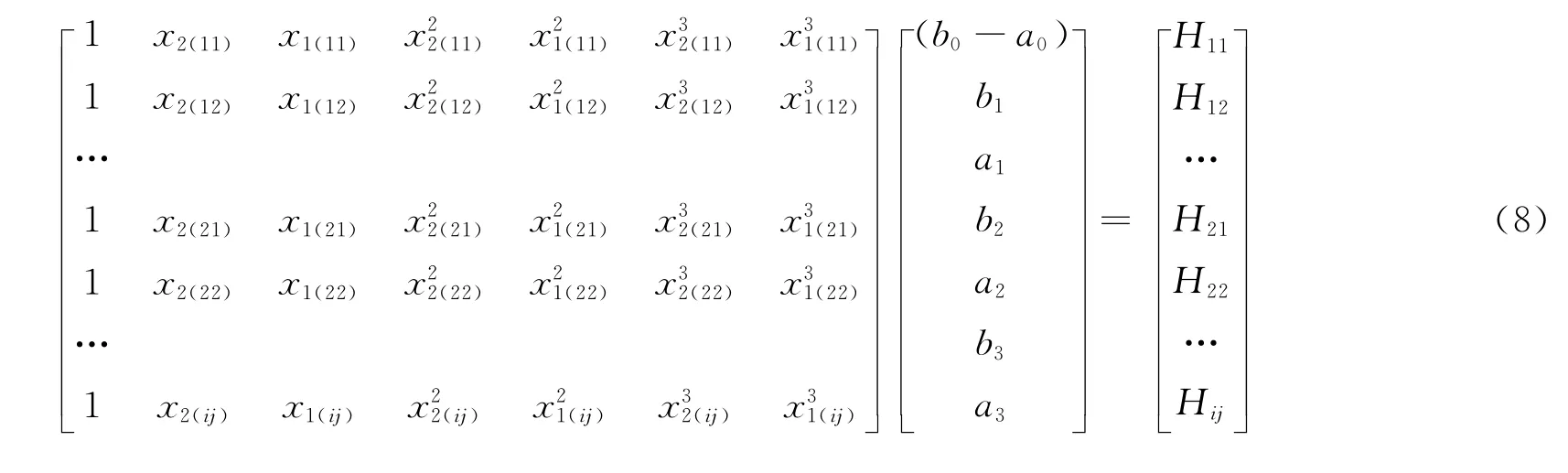
解此超定方程，得到系数（b0－a0），b1，b2，b3，a1，a2，a3的值。矩阵方程左边的系数矩阵为不同组别各次测量时成像光斑的横坐标值，等号右边的矩阵为被测物厚度真值。

依据上述推导，将20组标准厚度被测物沿1号到5号测量位依次测量若干组数据，得到一个包含i×j个方程的矩阵方程组，解此超定方程组，得到：（b0－a0）＝－3.050 2×10－1，b1＝3.411 9×10－3，a1＝－3.093 6×10－3，b2＝－8.720 6×10－8，a2＝－5.769 1×10－8，b3＝7.527 1×10－12，a3＝1.000 2×10－12。

2.2 校正前后数据分析

同样选定0.05mm，0.1mm，0.5mm，1mm，2mm，3mm六组被测物测量数据进行分析，拟合校正前后测量厚度—被测物位置关系曲线，拟合曲线如图7所示。

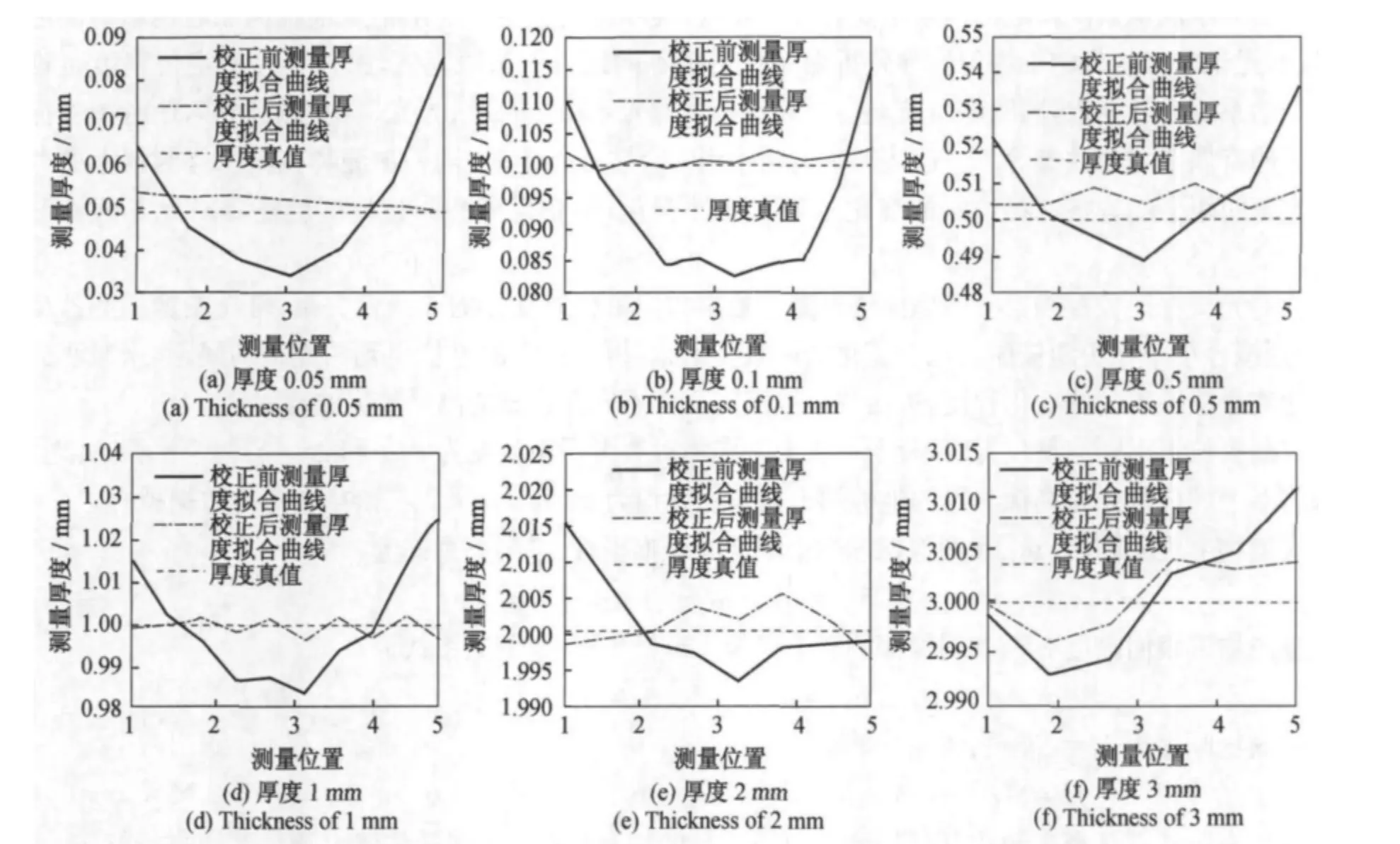
图7 测量厚度—测量位置拟合曲线Fig.7 The fitted curve of measured thickness vs.measured site

从图7中可以看出，测量厚度值波动程度变小，且最大波动约为7μm，远远小于校正前的最大波动量，测量误差减小，校正效果明显。

标准差σ表征同一被测量的n次测量的测得值分散性的参数，任一单次测得值对算术平均值的分散度越小，测量的可靠性就越大，即测量精度就越高［9］。标准差的计算公式为：

其中n为测量次数，δi为测量值与被测量真值之差。在6组对比实验中，校正前各组测量值的标准差分别为σ0.05＝0.017 6，σ0.1＝0.013 0，σ0.5＝0.017 4，σ1＝0.013 4，σ2＝0.006 7，σ3＝0.006 4。校正后的标准差分别为σ0.05＝0.002 6，σ0.1＝0.001 4，σ0.5＝0.006 5，σ1＝0.002 4，σ2＝0.002 9，σ3＝0.003 3。可以发现，校正后各组测量值的标准差明显变小，测量误差明显减小且数据分散度变小，测量精度明显提高。

3 结 论

针对单镜头激光三角法在测厚时因被测物位置变化对测量精度的影响提出了一种非线性校正方法，介绍了单镜头激光三角法厚度测量仪，包括其系统组成，测厚原理和光路结构，并对其标定方法做了介绍，对标定数据进行了分析，用得到的标定方程进行了精度校验评定。分析了单镜头激光三角法标定时存在非线性因素的原因，提出了一种校正方法，对该校正方法的数学模型进行了理论推导，并设计了一组对比试验，通过分析校正后标定方程的测量数据和校正前的标定方程的测量数据来评价校正效果，并对校正后的系统精度作了评定。研究结果表明，该非线性校正方法有效减小了被测物位置造成的非线性影响程度，明显减小了测量误差，提高了系统测量精度，同时对提高激光三角法在其它测量领域中的精度提供了一个参考措施。

［1］ 李晓天，张铁强，张胜勇，等.基于激光三角法的小物体尺寸测量及三维重构系统［J］.光学仪器，2008，30（6）：21－26.

［2］ 杨 程.基于CPLD技术的双光路补偿法玻璃测厚系统［D］.秦皇岛：燕山大学，2009.

［3］ 陈明君，谢大纲，李 旦，等.双路激光—CCD零件尺寸动态检测中的关键技术［J］.光电工程，2004，31（3）：33－36.

［4］ ZENG L J，YUAN F，SONG D Q.A two－beam laser triangulation for measuring the position of a moving object［J］.OpticsandLasers inEngineering，1999，31：445－453.

［5］ 熊志勇，赵 斌.激光三角法内孔测量传感器的光学成像分析［J］.光学仪器，2011，33（5）：85－89.

［6］ 黄战华，蔡怀宇，李贺桥，等.三角法激光测量系统的误差分析及消除方法［J］.光电工程，2002，29（3）：58－61.

［7］ 郁道银，谭恒英.工程光学［M］.北京：机械工业出版社，2009：20－25.

［8］ 沙定国，苏大图.光学测试技术［M］.北京：北京理工大学出版社，2010：19－32.

［9］ 廖念钊，古莹蓭，莫雨松，等.互换性与技术测量［M］.北京：中国计量出版社，2007：46－54.