热羽流盐水模型实验研究综述

王昕 梁云 代运天

上海理工大学环境与建筑学院

0 引言

热羽流是一种常见的对流现象[1]。从电子元件、发热设备和人体上方上升的热空气，到火灾时上升的热烟流，以及工业烟囱中释放的烟羽流，热羽流以各种可见和不可见的形式存在于自然环境中[2]。自20世纪60年代羽流理论建立[3]以来，研究者们对羽流进行了大量的研究，这些研究不仅发展和完善了羽流理论，而且拓宽了羽流理论的应用领域。例如，火灾科学中烟羽流的蔓延发展规律，通风工程中热羽流作用下室内空气分布规律。为了验证羽流相关理论及其应用领域的相关理论，研究者们通过各种实验手段或方法对羽流现象进行了研究，其中盐水模型实验一直是备受青睐的实验方法。

本文将对盐水模型实验方法进行简要介绍，并对其在羽流研究中的应用进行总结，同时针对盐水模型实验方法的技术难点进行探讨。

1 盐水模型实验原理

1.1 盐水模型实验

盐水模型实验研究方法是一种以相似理论和模型实验技术为基础预测气流运动的研究方法，它具有真实直观、经济高效、条件易控和环境友好等优点。用盐水模型实验方法研究室内气流运动特性，可以直观地观察到流体的运动形态，实现流动可视化研究。因为空气的运动粘性系数约是水的15倍，所以在缩尺模型实验中易于达到与原型相同的相似准则数，而且由于空气模型实验中忽略了粘性的影响，严格地说空气模型实验的室内温度场是不可能实现相似的[4]。

在热羽流理论及应用研究中，盐水模型实验一直是备受研究者青睐的实验方法，它根据盐水扩散运动与热羽流运动的相似性，利用盐水在缩尺模型中模拟热羽流的运动过程，具有独特的优势。

1.2 盐水模型实验原理

1.2.1 相似性分析

在热羽流运动过程中，不断卷吸周围环境空气，同时进行对流热交换。由于空气中的温度分布不均匀，使气流间形成密度差，导致冷热气流之间产生相对运动现象[5]。盐水溶液在清水中运动时，由于存在浓度差，形成对流传质现象。由于清水和盐水之间的浓度差（密度差），导致盐水和清水之间产生相对运动现象。这种现象与空气中非等温气流运动现象的原理一致。盐质在清水中的对流扩散现象与空气中非等温气流运动现象的原理一致，且现象相似，即空气的温度场与盐水的浓度场相似。

在笛卡尔坐标系下分析气流运动和盐水扩散运动的控制方程可知，盐水运动的浓度扩散方程和室内气流运动的连续性方程、运动方程和能量方程相似，即两种运动的控制方程组是相似的。

1.2.2 相似准则的确定

在满足几何相似的前提下，选取适当的特征量，分别将气体运动的控制方程和盐水运功的控制方程无量纲化，可以分别推导出气流运动的准则数（Re，Fr，Pr）和盐水运动的准则数（Re，Fr，Sc）。

由相似理论[6]可知，当这两种运动的Re，Fr和Pr与Sc相等时，二者的无量纲化控制方程组完全相同，这表明由控制方程所描述的这两种运动形式是相似，即这两种运动相似的相似准则是Re，Fr和Pr（Sc）。在满足相似准则的情况下，用盐水模型实验模拟热羽流运动是可行的。

2 热羽流基础实验研究

2.1 羽流研究早期应用的空气模型实验

在经典羽流理论建立之前，Schmidt在均匀空气环境下对电加热网格产生的热羽流的温度分布和速度分布进行了测试，其利用热线测试得到的流速无法测得竖直方向的速度分量，而温度测试结果显示，温度分布曲线呈现标准正态分布[3]。

Rouse在均匀空气环境下对不同热源强度的点源和线源产生的热羽流的温度分布和竖直方向速度分布进行测试，通过对不同高度的温度分布和竖直方向速度分布的测试，得到了这两种热源形式产生的羽流的竖直方向速度分布和浮力分布的无量纲形式。对于点热源，Rouse根据测试测试结果，选择exp(-96r2/x2)和exp(-71r2/x2)作为竖直方向速度分布和浮力分布，因为二者的测试结果分别与这两个分布曲线吻合较好[3]。

2.2 经典羽流理论中的盐水模型实验

在Schmidt等研究者对羽流进行初步研究的基础上，Morton、Taylor和 Turner（以下称 MTT）于 1956年建立了经典羽流理论[3]。MTT通过理论建模，得到了不同羽源条件和不同环境条件下的羽流运动的几何特征、速度分布和浮力分布特性。

MTT采用液体模型实验验证其羽流理论模型，实验在直径为300mm，高1000mm的水箱中进行的。通过从水箱底部把密度相对较小的甲基化酒精注入到密度相对较大的静止分层的盐溶液中，模拟热羽流在分层环境中的运动。用玻璃泡放入水箱盐溶液中，测定玻璃泡悬浮的高度，可以得到该高度水平面内盐溶液的密度，利用不同密度的玻璃泡可以测得的水箱中盐溶液在竖直方向上的密度分布。MTT的盐水模型实验如图1[3]所示，通过模型实验的测试技术，可以测得热羽流运动相关的流场参数，同时可以清晰地观察羽流的运动发展过程，为直观地认识羽流的运动特征提供了良好的研究手段。

图1 盐水模型实验中的热羽流

2.3 羽流理论发展过程中应用的盐水实验

Baines在1983年提出一种测试羽流流量的新方法[7]，并利用盐水模型实验对该方法进行了实验验证。实验水箱尺寸为320mm×320mm×510mm，具有微小压头的清水从水箱上部的多管分布器中向水箱中缓缓注入，清水系统装有流量计用于计量清水流量Q1。用于模拟热羽流的盐水从水箱顶部注入，注入口内部装有微孔格栅，以保证盐源以紊流流态注入，盐源注入的流量为Q0。

实验示意图如图2所示，实验中清水和添加有颜料的盐水分别以设定流量注入水箱中，其中清水流量Q1与盐源流量Q0相比要小得多。盐水将以与热羽流相似的形式在水箱中运动，经过一段时间，在z=zi的位置将产生稳定的分界面。通过改变清水的流量Q1，分界面的位置zi将发生变化，因而可以得到羽源流量为Q0时不同高度z处的羽流流量。

图2 羽流流量测试实验示意图

3 热羽流虚源的处理

对于点热源形成的热羽流来说，其初速度为零，但在盐水模型实验中，作为模型实验中重要边界条件的羽源注入口却无法实现零初速和点源，模拟羽源的介质总是从一定尺寸的注入口中以一定的流速流出的，也即虚源点是在羽流注入口后方某一位置处。为了尽可能降低实验中羽流的初速度以及准确地确定虚源点的位置，研究者们进行了大量工作设计实验装置，同时提出一系列点源位置的修正方法。

3.1 注入口装置的设计

在盐水模型实验中，既要保证盐水注入的速度尽量小，同时又要保证盐水以湍流状态注入，这是一对矛盾，需要通过科学合理的设计注入口装置来解决。另外，在经典羽流理论的三个假设条件中，不同高度截面速度分布和浮力分布相似是最关键的一个，其中速度和浮力的分布有高斯分布（Gaussian profile）和高帽分布（Top hat profile）两种假设[8]，二者的分布形式如图3所示。高帽分布假设以其简便性得到了广泛的应用，而且大量研究结果表明，高帽分布假设能较好地描述羽流的运动发展情况。在模拟热羽流的盐水模型实验中，多数研究者都通过设计羽流注入装置使羽流的注入口速度分布符合高帽分布假设。

目前在热羽流盐水模型实验中应用最广泛的羽源注入口装置是由Paul Cooper设计的，装置结构如图4所示。盐溶液首先流过一个狭窄的开口（d1=0.1cm），然后流经一个相对较大的圆柱形空腔（D=1.0cm，L=1.2 cm），最后经过一层致密的筛网从管口（d2=0.5cm）处流出，注入清水中。

图3 羽流速度和浮力分布的两种形式

图4 点羽源注入口装置示意图

3.2 羽流虚源位置的修正

通过对实验装置的改进只能尽可能减小羽源的初速度，无法实现初速为零。为了保证羽流的流量，在减小羽流初速度的同时，还必须使羽流注入口具有一定的尺寸。另外，如果一味地减小羽源的初速度，则无法保证羽源介质以湍流流态进入环境空间。基于以上实验条件的限制，还必须对虚源点的位置进行修正。

对于虚源位置的修正，研究者们进行了大量的研究[3，9～11]，提出了一系列修正方法：①基于实验数据的修正；②基于圆锥流形的修正；③基于羽流状态的修正；④基于羽源参数（F0、M0、Q0）的修正；⑤基于 Γ 的修正。

3.2.1 基于实验数据的修正

通过实验测试结果来确定虚源的位置是容易实现的。MTT提出这样一种方法，就是根据某一实验测试参数数值随轴向距离z在z＞0情况下的变换规律来推算z＜0处的数值。另一种利用实验数据确定虚源位置的方法是由Baines和Turner在1969年提出的[9]，该方法是通过羽流产生初期羽流前锋的位置与时间的函数关系来确定虚源点位置的。

3.2.2 基于圆锥流型的修正

Schmidt在1941年提出羽流的整体流型呈现倒圆锥形分布，这一结论也被大量实验室实验和自然环境观察的羽流情况所验证。基于此圆锥流型和经典羽流理论，MTT提出一种确定虚源点的简易方法[3]。通过引入一个有效羽流半径来确定羽流的外边界，从而通过确定圆锥形外边界的顶点位置可以确定虚源点位置，羽流的圆锥形结构如图5所示。

图5 羽流的圆锥形结构示意图

3.2.3 基于羽流状态的修正

对于实验中发生的羽流来说，都是具有一定初始流速的受迫羽流。Morton指出[10]，受迫羽流在发展过程中，经过一段距离之后，其特征逐渐趋于纯羽流，即运动由初始动量主导转变为由浮力主导。而判断是否发展成为纯羽流的标准为：

式中：Q 为羽流流量，m3/s；F 为羽流浮力通量，m4/s3；M为羽流动量，m4/s2；α为卷吸系数。

由受迫羽流发展为纯羽流的位置为：

其虚源点的位置zavs可由下式确定：

3.2.4 基于羽源参数（F0、M0、Q0）的修正

Morton在1959年提出了一种在理论上确定虚源位置的方法[10]。Morton 将羽源（F0、M0、Q0）在 z=0 处的流动参数与等效的点源（F0、γM0、0）在 z=zv处的流动参数联系起来，二者满足相同的控制方程。通过理论推导，得到了对于纯羽流和受迫羽流的虚源位置修正：

纯羽流：

受迫羽流：

式中：γ5=1-Γ。

3.2.5 基于Γ的修正

由羽流运动的控制方程组，Hunt和Kaye得到[11]：

其中：

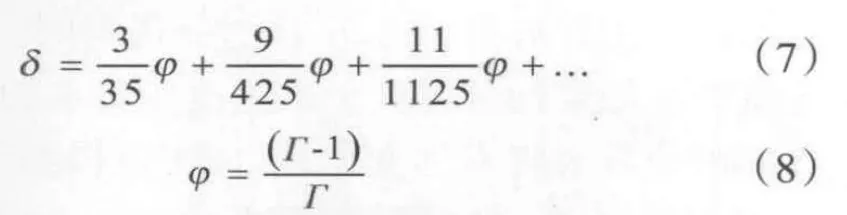
无量纲参数Γ由羽源的情况确定：

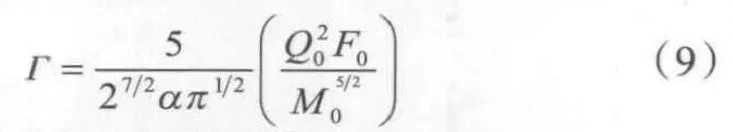
于是可以得到虚源的位置修正：

4 在通风工程及火灾科学中的应用

4.1 热压作用下自然通风的盐水模拟

盐水模型实验在预测室内气流分布领域中的应用，最著名的当属Linden等人在1990年对置换式自然通风的研究[12]，首次提出了“Emptying Filling Box”自然通风模型，阐述了室内二区置换式自然通风的流动机理，并通过盐水模型实验验证了开口流速的理论表达式以及单个点源和单线源的热分层界面位置的表达式，其置换式自然通风的实验如图6[12]所示。

图6 置换式自然通风的实验

P.F.Linden和P.Cooper发展了前期研究成果[13]，采用理论方法研究了含有两个和多个点热源羽流的自然通风模型，但没有考虑羽流之间的相互作用，依然应用盐水模型实验法进行了验证。2006年，N.B.Kaye和P.F.Linden利用盐水模型实验的方法，在同一水箱中同时模拟三种不同密度的流体的相对运动，对上下对应的冷热气体射流的运动特性进行了研究，对相向运动的射流相互作用进行了分析[14]。J Oca利用盐水模型实验的方法研究了温室通风，实验中专门针对盐水模型实验进行了相关研究，评估了Re对盐水模型实验的影响，而且还重新评估了在盐水模型实验中可以忽略粘度影响的Re范围[15]。

哈尔滨工业大学王磊等利用盐水模型实验方法对热压驱动下的自然通风进行研究[4，16]，利用盐水模型实验技术来模拟室内热羽流运动引起的室内热分层现象，预测了热压驱动下自然通风房间内热分层高度、温度分布和通风量的变化规律，实验还考虑羽流之间的相互作用，验证了多股热羽流的叠加效应，其实验台实物图如图7[4]所示。

图7 自然通风盐水模型实验装置

4.2 火灾烟羽流盐水模拟

盐水模型实验方法在建筑火灾科学研究中的应用也很广泛，但早期的盐水模拟实验大多用于定性研究[17]。Thomas曾于1963年用盐水模拟技术来显示顶棚和侧壁的排烟口向大房间里排烟的效果，Tangren等人也于1978年运用该方法在1:5模型里研究带有走廊或窗口的房间火灾所产生的热烟气层密度和位置。C.M．F1eischmann和 P.J．Pagni等人建立的盐水模拟实验台，所作的初步研究仅用于观察盐水流从不同出口的房间向走廊流出所形成的顶棚射流和分层流的锋面结构、形状和运动速度[18]。

中国科技大学火灾实验室在1993年设计建立了我国第一座盐水模拟实验台[17]，其主水箱尺寸为1.5m×1.0m×1.0m。与国外同类实验台相比，该实验台功能完善、结构新颖、造价低廉，解决了烟源强度和位置的模拟、盐水液面位置稳定等问题，提高了实验测量精度，扩大了测量范围，并首次成功引入氢气泡显示测量技术。

从1993年到1996年底，运用该实验台完成了多项研究课题，研究范围涉及受限空间烟羽流准稳态结构和蔓延规律、顶棚射流和顶棚下分层流的发生发展过程、侧室走廊烟气和卷吸空气的运动规律[19～21]。他们还首次将盐水实验模拟方法用于中庭类型建筑物内的火灾烟气运动规律研究，着重模拟了侧室火灾烟气经走廓流向天井及其在天井内的运动持性。

5 结论和展望

热羽流的羽源特征是影响羽流特性的最重要参数，针对盐水模型实验中羽源的出流特征与实际热羽源不符的情况，研究者们进行了大量的工作来设计实验装置，同时提出一系列点源位置的修正方法，尽可能降低实验中羽流的初速度以及准确地确定虚源点的位置。通过修正后的实验结果可以较好地反应实际羽流的运动特性。

随着相似理论的逐步完善和实验技术的发展，热羽流盐水模型实验从最初的仅用于观察研究和定性研究，逐步发展到后来可通过间接测量得到一定的定量参数。目前，结合最新实验测试技术（如PIV粒子图像测速法等）盐水模型实验也得到比较全面的热羽流和其它类型气流流场参数。

热羽流盐水模型实验在通风工程技术研究以及火灾科学研究等领域得到了广泛应用，热羽流盐水模型以其独特优势，在热羽流理论研究以及工程技术研究中将发挥重要作用。

[1]G K.Heat convection and buoyancy effects in fluids[J].Q.J.R.Met.Soc.,1954,80,339-358

[2]G R Hunt,T S van den Bremer.Classical plume theory:1937-2010 and beyond[J].IMA J Appl Math.,2011,76:424-448

[3]B R Morton,G I Taylor,J S Turner.Turbulent gravitational convection from maintained and instantaneous sources[J].Proc.R.Soc.Lond.A,1956,234:1-23

[4]王磊.热压驱动下的置换式自然通风实验研究[D].哈尔滨:哈尔滨工业大学,2006

[5]李炜,槐文信.浮力射流的理论及应用[M].北京:科学出版社,1997.

[6]李之光.相似与模化[M].北京:国防工业出版社,1982

[7]W D Baines.A technique for the direct measurement of volume flux of a plume[J].J.Fluid Mech.,1983,132:247-256

[8]Peter Lin.Plumes and Jets in Semi-confined Spaces[D].Californi-a:University of California,2003

[9]W D Baines,J S Turner.Turbulent buoyant convection from asource in a confined region[J].J.Fluid Mech.,1969,37:51-80

[10]B R Morton.Forced plumes[J].J.Fluid Mech.,1959,(5):151-163

[11]G R Hunt,N G Kaya.Virtual origin correction for lazy turbulent plumes[J].Journal of Fluid Mechanics,2001,435:377-396

[12]P F Linden,G F Lane-Serff,D A Smeed.Emptying filling boxes:the fluid mechanics of natural ventilation[J].Journal of Fluid Mechanics,1990,212:309-335

[13]P F Linden,P Cooper.Multiple Sources of Buoyancy in a Naturally Ventilated Enclosure[J].Journal of Fluid Mechanics,1996,311:177-192

[14]N B Kaye,P F Linden.Colliding turbulent plumes[J].Journal of Fluid Mechanics,2006,550:85-109

[15]J Oca,J I Montero,A Antón,et al.A method for studying natural ventilation by thermal effects in a tunnel greenhouse using laboratory-scale models[J].Agriculture Engineering Research,1999,72:93-104

[16]高军.建筑空间热分层理论及应用研究[D].哈尔滨:哈尔滨工业大学.2007

[17]张和平.火灾烟气运动盐水实验模拟和受限空间初起火灾烟气运动特性的研究[D].合肥:中国科学技术大学,1996

[18]C M Fleischmann,P J Pagni,R B Willianmson.Salt water modeing of fire compartment gravity Currents[A].In:Fire Safety Scien-ce Proceedings of the Fourth International Symposium[C].1994:253-264

[19]张和平,周晓冬,万玉田,等.受限空间烟气运动盐水模拟研究的现状和展望[J].中国安全科学学报,1999,19(1):30-34

[20]张和平,张人杰,麻柏坤,等.建筑物内火灾烟羽流和顶蓬射流诱发的空气运动盐水模拟实验研究[J].实验力学,1997,12(1):70-79

[21]张和平,姜锡权,谢之康,等.中庭建筑天井内火灾烟气运动特性的盐水实验模拟[J].实验力学,1994,14(1):69-79