对应分析在大学生听课效果评价中的应用
□文/韩大平
(德州学院经济管理学院 山东·德州)
分析记笔记方式与成绩间的相互关系常用描述统计和相关分析。在描述统计中,用得较频繁的是频度统计、平均数、百分数等统计量。但这些统计量仅能进行单变量数据描述,并且数据拘泥于就事论事的罗列,不能对数据进行挖掘。相关分析可以挖掘多变量间的关系,如关联的程度和方向,也可用于信度分析、预测等,是一种功能强大的多用途统计技术。本文介绍的对应分析法,即能形象地用二维坐标图表达出两个变量不同分类间的关系,这是其他方法所难于比拟的。
本次研究的数据,来自由德州学院2012级国际经济与贸易学专业组织的针对全校四个年级各专业学生的学习方式调查。数据采用问卷形式获得,用系统抽样方法从全校四个年级的学生中抽取146人,收回133份调查问卷,对数据进行处理,经剔除重复数据,并使用序列均值方法替换缺失值后得到123份有效调查问卷,旨在了解学生学习方式与学习成绩之间的关系。但本次分析的数据只研究其中的一个变量,即:学生上课记笔记方式与学习成绩的关系。记笔记的方式分为四个层次:不停地记笔记,课后再复习;认真听老师讲解,偶尔记笔记;不听老师讲解,自己看书学习;只听老师讲解,从不记笔记,并分别赋值1、2、3、4。对被调查者分数重新编码,将学生成绩分为四个层次:0~59.9分,60~69.9分,70~79.9分,80~100分,分别赋值1、2、3、4。具体的研究问题是:记笔记方式与学习成绩变量类别之间是否有联系?如果有联系,联系有什么趋势?
在对调查数据进行分析和重新编码的基础上对行变量类别与列变量类别进行交叉汇总,如表1所示。(表1)
样本量为123人。总体上看,大多数回答情况是不停地记笔记,课后再复习和认真听老师讲解,偶尔记笔记,两项共计106人。70~80分的学生为54人。(表2)
表2显示对应分析最终汇总统计量,包括维度、单一值、惯量、卡方值、p值、惯量解释比例以及单一值稳定性等数据。卡方值19.507,p=0.021<0.05,表明学习方式与学习成绩之间有显著的依赖关系。第一项是维度,其缺省值是2。单一值是各维度对变量各个类别之间差异的解释量,代表每一维度的行分值与列分值的相关系数。数据0.322就是第一维度的行分值与列分值的相关系数。惯量即相应维度单一值的平方,它表示每个维度对各个变量类别之间差异的解释量。解释比例即每一维度惯量在总特征值中的比例。在表2中,第一维度的解释比例为65.2%,说明第一维度能够解释所有变量类别差异的65.2%,第二维度的解释比例为32.9%,能够解释所有变量类别差异的32.9%,而第三维度的解释比例为1.9%,仅能够解释所有变量类别差异的1.9%,因此可以认为用两个维度就可以解释行列变量之间所有的关系。这一指标可以帮助确定用于分析的维度数。总惯量19.507÷123=0.16,满足总惯量和χ2统计量的关系式。同时,χ2统计量的自由度9=(4-1)×(4-1),数值为0.021,说明行列变量之间存在显著的相关性,相应分析是有意义的。
对应分析还能用图形直观地反映行变量与列变量之间的关系,特别是当变量的类别数多时,图形既直观又具解释力,优势更加突出。本次分析的图形结果见图
1。(图1)
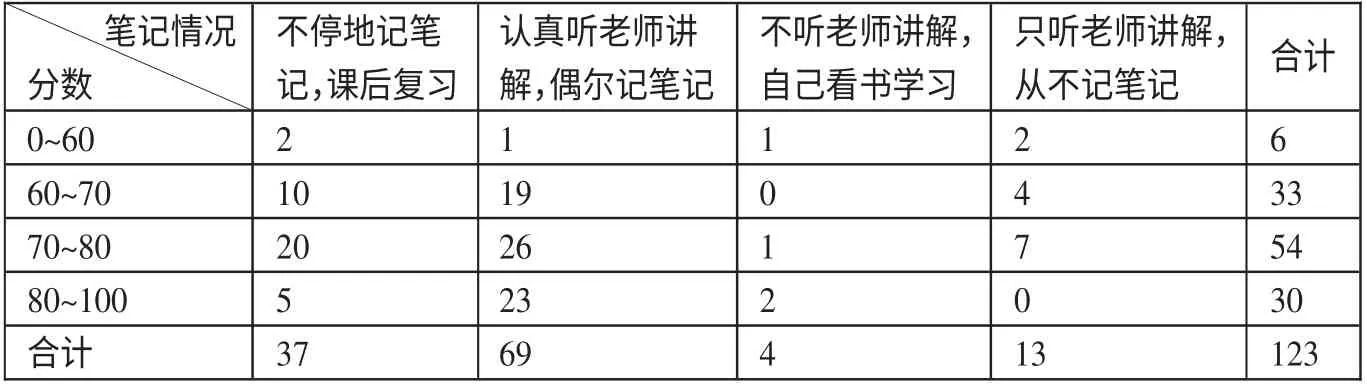
表1 记笔记方式与成绩的交叉汇总表

表2 显示对应分析最终汇总统计量
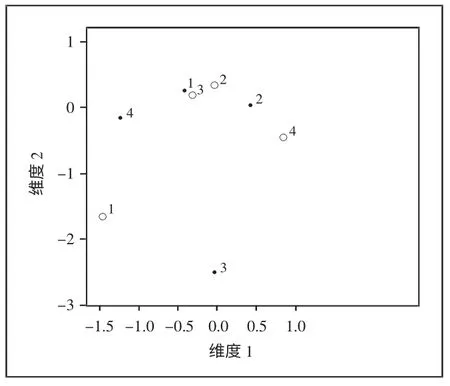
图1 相应分析的二维图
注:图中实心的圆点表示记笔记情况,空心的圆圈表示成绩。不停地记笔记,课后再复习=1;认真听老师讲解,偶尔记笔记=2;不听老师讲解,自己看书学习=3;只听老师讲解,从不记笔记=4。0~60分=1,60~70分=2,70~80分=3,80~100分=4。
图1可以同时达到两个目的:一是解释变量间的关系,二是帮助分析变量分类的合理性。在图1中,分值的距离表示变量间的差异,有相似分布的变量在距离上靠得近一些。如果分值是负数,说明这一单元格的观察频数低于期望频数。从图1可看出,70~80分与不停地记笔记,课后再复习联系紧密,80~100分与认真听老师讲课,偶尔记笔记联系紧密。整体而言,及格以上的学生更倾向于不停地记笔记,课后再复习或认真听老师讲课,偶尔记笔记。从图1还可看出,在变量的分类上,70~80分可以与60~70分合并为60~80分。而不及格的学生与其他人相差甚远,他们不听老师讲解,自己看书学习或只听老师讲解,从不记笔记。
综合以上分析,我们可以得出下列结论:学生学习成绩与上课记笔记方式有联系:学习成绩较好的学生倾向于认真听老师讲课,偶尔记笔记或不停地记笔记,课后再复习。而学习成绩差的学生则不听老师讲解,自己看书学习或只听老师讲解,从不记笔记。
一般的交叉表难以清晰地表达两个变量的本质关系。本文以对应分析法分析大学生记笔记方式与成绩间的二维对应关系,并能输出几何坐标图,形象地表达一般交叉表难以表达的变量不同分类间的关系。相似的分类变量才会在坐标图上彼此靠近,因而很容易形象地了解变量的哪些分类间彼此相似或彼此相关。因此,在分析学习方式对学习成绩的影响中学会对应分析方法不仅有利于提高学生学习成绩,也有助于推动这类研究向纵深发展。
[1]潘宝骏,陈征,刘少娟.8463例正常分娩新生儿体重、胎位与孕母年龄的对应分析[J].中国卫生统计,1999.3.
[2]汪顺玉.SPSS对应分析在外语学习需求分析中的运用[J].重庆邮电学院(社会科学版),2004.5.
[3]苏艺,许兆义,鄢贵权.对应分析方法在地下水环境系统分析中的应用[J].北方交通大学学报,2004.8.

