基于支持向量机的发电机匝间转子绕组短路故障诊断

朱志宇，耿 璜，瞿 盛

（江苏科技大学 电信学院，江苏 镇江 212000）

转子绕组匝间短路是发电机的一种常见电气故障，当转子绕组发生匝间短路时，将使转子电流增大，绕组温度升高，限制电机的无功功率。轻微的匝间短路故障机组仍可继续运行，但是一旦故障恶化会导致转子一点甚至两点接地等恶性故障的发生。

近年来，神经网络在复杂非线性系统的故障诊断领域中得到了广泛应用[1]，但由于这项技术缺乏坚实的理论基础，而且神经网络存在一些诸如收敛速度慢、局部极小点、过学习与欠学习以及需要大量的故障数据典型样本等不足，制约了人工神经网络在智能故障诊断中进一步应用和发展。

支持向量机（support vector machine，SVM）是在统计学理论基础上发展出的一种性能优良的模式分类方法，既有严格的理论基础，又能较好地解决小样本、非线性、高维数和局部极小点等实际问题[2]。

在此，将支持向量机方法应用于匝间转子绕组短路故障诊断，建立了基于支持向量机的多故障分类器，并与BP神经网络分类器进行比较。

1 支持向量机原理

统计学习理论是 （SLT）在V.VAPNIK在20世纪70年代末提出的一种有限样本统计理论，是针对小样本统计理论而建立的一套新的理论体系[3]。统计学习理论给出了结构风险最小化原理和VC维 （Vapnik-Chervonenkis Dimension）的概念，指出经验风险最小不能保证期望风险最小，提出为了最小化期望风险，必须同时最小化经验风险和VC维[3]。从线性可分模式的情况来看，它的主要思想就是建立一个超平面作为决策面，该决策面不但能够将所有训练样本正确分类，而且使训练样本中离分类面最近的点到分类面的距离最大。

设样本集 D={（xi，yi）|i=1，2，…n}，x∈Rdiy∈{+1，-1}则其超平面方程WT+b=0（其中w是权向量，b为偏置），其优化问题可描述为在满足

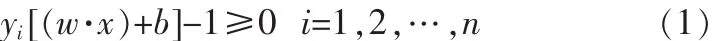
这个优化问题可以采用Langrange法，利用对偶原理将原问题转变为在满足

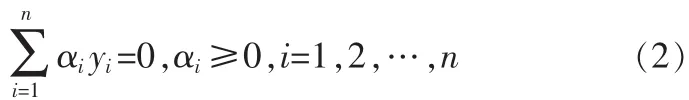
的约束条件下求解

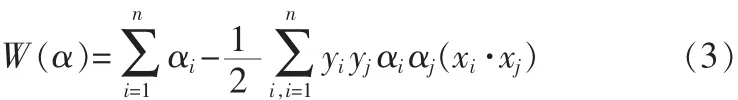
的最大值。

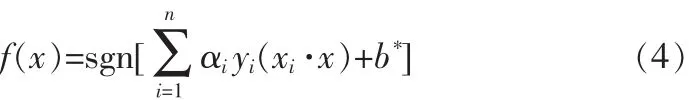
对于非线性不可分的情况下，可通过非线性变化将输入空间映射到某个高维空间，使其成为线性可分，并在高维空间中得到最优分类超平面，这种非线性映射函数也称为核函数。设存在一个非线性映射φ（*）：Rd→Rh将输入空间样本映射到高维空间，则核函数可表示为

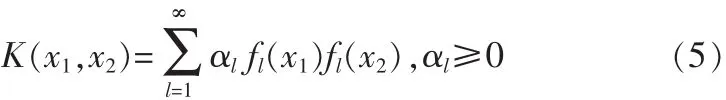
相对于线性可分模式此时的约束条件为：

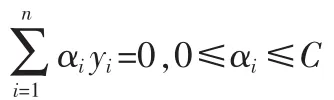
最优分类决策函数为：

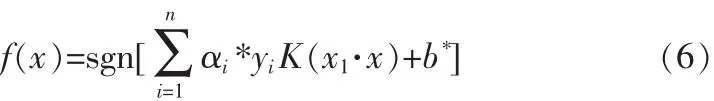
2 基于SVM的匝间转子绕组短路故障诊断

2.1 故障特征样本的提取

发电机在正常运行时感应电动势的信号可表示为e（t）=s（t）+w（t），式中 s（t）为主磁通产生的感应电动势，是基频分量；w（t）是转子漏磁通产生的感应电动势，属于高频分量，通过检测这部分高频分量可以判断转子是否发生发生匝间短路。小波包技术能将信号无冗余、无疏漏、正交地分解到独立的频带内，这些分解频带信号都具有一定的能量。本文用小波变换对信号进行预处理[4]，然后将信号分解到相互独立的频带内，然后对各频带的信号分别进行小波分解，系数重构，从而提取特征向量，作为故障诊断的特征值。

2.2 故障分类器的选择

支持向量机最初是针对二值分类问题提出的，而匝间短路的故障类别不止两类。

目前能实现支持向量机多分类的常用方法有两种：一种是“一对多”方法，即用一个分类器将一种类别的模式与剩下的所有类别的模式区分开，因此对于类问题需要构造个故障分类器。这种方式的缺点是对每个分类器的要求比较高。另一种是 “一对一”方法，即分别选取两个不同类别并构成一个SVM子分类器，分别构造k（k－1）个子分类器，在进行故障识别时，对这个分类器进行测试，并累计各类别的得分，选取得分最高者所对应的类别为测试数据的类别。这种方法的缺点是在故障模式较多的情况下需要构造的分类器过多，测试时需要对每个SVM都要进行比较，导致测试速度慢[5]。经综合考虑，文中选用“一对多”的方法建立分类器来匝间转子绕组进行短路故障识别。

2.3 训练与诊断步骤

假设有类故障，则用SVM进行故障诊断的步骤如下：1）训练阶段

Step1：利用小波分析得到匝间转子绕组短路故障特征信号，建立训练样本集{xi，yi}，yi∈[－1，1]。

Step2：选择合适的核函数 K（x，y），及有关参数，作为高维特征空间在低维输入空间的一个等效形式。

Step3：根据Kernel函数的要求，将输入样本正规化。

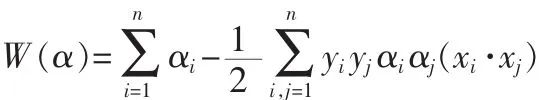
以求解出出拉格朗日系数α。

Step5：找出支持向量sv，求解分类超平面系数b*。

Step6：建立训练数据的最优决策超平面，训练结束。

2）诊断阶段

Step1：装入 SVM 学习阶段有关的数据（包括{xi，yi}，α，b，sv）。

Step3：利用指示函数，将 f（x′）归为[－1，1]，做出决策分类。

2.4 实验与分析

在实验过程中，以某隐极式32槽的转子为诊断对象，主要针对转子的3种运行状态：正常运行、10%匝间短路、20%匝间短路。通过探测线圈采集3种状态下的特征信号各40组。按照前述方法选择每种情况下的10组数据（其余30组为作为测试样本），对其进行三层db3小波分解，提取出故障特征向量作为训练样本的输入，将其中某种样本的输出置为1，其余的两种样本的输出置为－1。

SVM的参数对其性能有很大影响，目前还没有一个统一的方法来决定SVM参数的最佳取值，一般的选择方法是试凑法[6]，文中核函数选用d=3的多项式核函数，并在此基础上经过分析比较将约束常数C的值设为1 000，然后进行样本训练，求出最优分类决策函数。同理可以分别建立对应于3中运行状态的3个故障分类器SVM1～SVM3。在分类测试中，先提取出测试数据的故障特征向量x，然后将其输入故障分类器，若SVM1的判别式输出为1，即测试样本到H的距离为正数，则确认为正常状态；否则自动输入给分类器2，若SVM2的判别式输出为1，则确认为10%匝间短路；否则自动转入判别式3，若SVM3的判别式输出为1，则确认为20%匝间短路；否则出现其他故障类别。表1是对3种运行状态下各取3组数据进行分类的结果，从中可以看出支持向量机对匝间短路进行故障诊断是有效、可行的。

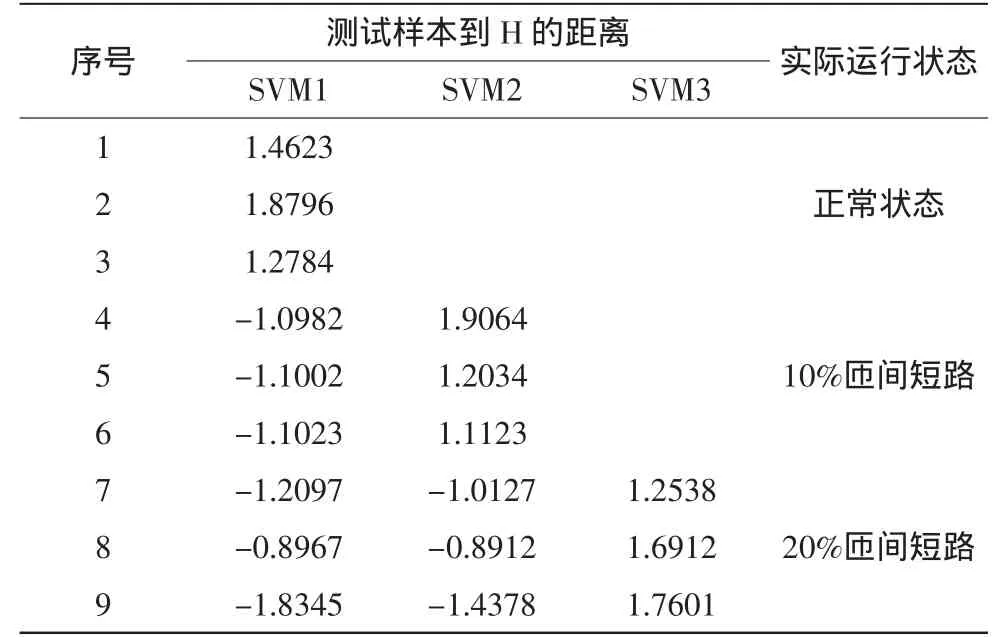
表1 对测试样本的分类结果Tab.1 Classification result of testing samples

下面将比较支持向量机和常用的人工神经网络的分类效果，根据特征向量的位数和匝间短路的故障状态数设计BP神经网络，该神经网络的输入层和输出层的节点数位6和4，隐层节点数选取为8，隐层和输出层的激活函数选用sigmoid型函数。设定最大训练步数为5000，误差指标分别为0.02、0.01、0.05，采用与支持向量机相同的训练样本和测试样本对该BP网络进行训练和测试。比较结果如表2所示，从中可以看出，在训练样本数量和质量相同的情况下，采用支持向量机进行故障诊断的正确率明显高于BP神经网络，而且BP神经网络不仅准确率不高，还出现了过学习的现象。同时也看到，核函数的不同对支持向量机的分类准确率也是有影响的，所以在实际应用应当选择合适的核函数及其参数。

表2 支持向量机与BP神经网络的分类比较结果Tab.2 Result of comparing SVM and BP neural network

3 结束语

文中提出的一种基于支持向量机的匝间转子绕组短路故障诊断方法，对其3种状态进行了故障分类，实验结果表明，与常用的BP神经网络相比，支持向量机具有更高的准确率，能更好的解决小样本情况下过学习的情况，在故障诊断中有较好的应用前景。

[1]黄泉水，江国和，肖建昆.基于AR模型和神经网络的柴油机故障诊断[J].振动、测试与诊断，2009，29（3）:362-365.HUANG Quan-shui，JIANG Guo-he，XIAO Jian-kun.Fault diagnosis of diesel engine based on AR model and neural network[J].Journal of Vibration， Measurement&Diagnosis，2009，29（3）:362-365.

[2]何学文，赵海鸣.支持向量机及其在机械故障诊断中的应用[J].中南大学学报，2005，36（1）:98.HE Xue-wen，ZHAO Hai-min.Support vector machine in the application of machine fault diagnosis[J].Journal of Central South University，2005，36（1）:98.

[3]Vladimir N.统计学习理论的本质[M].张学工，译.北京:清华大学出版社，2000.

[4]王计生，喻俊馨，黄惟公.小波包分析和支持向量机在刀具故障诊断中的应用[J].振动测试与诊断，2008，28（3）:273.WANG Ji-sheng，YU Jun-xin，HUANG Wei-gong.Fault diagnosis of tool based on wavelet packet analysis and support vector machine[J].Journal of Vibration，Measurement&Diagnosis，2008，28（3）:273.

[5]孙永奎，陈光，卒禹，等.支持向量机在模拟电路故障诊断中应用[J]．电子测量与仪器学报，2008，22（2）：72-75.SUN Yong-kui，CHEN Guang，ZU Yu，et al.Fault diagnosis of artificial circuit based on support vector machine[J].Journal of Electronic Measurement and Instrument，2008，22（2）：72-75.

[6]肖凡，郭阳明，马捷中.基于参数优化支持向量机的航空电子系统故障诊断[J].计算机测量与控制，2012，20（3）:564.XIAO Fan，GUO Yang-min，MA Jie-zhong.Fault diagnosis of avionics system based on parameter optimization support vector machine[J].Computer Measurement Control，2012，20（3）:564.