仿真试验条件下飞行器外部静态磁环境模拟

还迎春 林春生 余 杰

（海军工程大学兵器工程系 武汉 430033）

在进行磁干扰补偿模型系数求解时，一般要求飞机首先进行四航向机动学习飞行，用时几十min，然后将学习样本数据用于模型系数求解［1］．这种方法不适合在要求快速反应的飞行器上使用．根据飞行器载体磁干扰的产生机理，研究在实验室条件下对飞行器载体磁干扰补偿模型系数精确求解的方法，为飞行器磁干扰补偿模型求解提供一种不依赖于机动飞行学习的实用方法，省掉飞行器的学习飞行时间，对保证装备的快速反应能力有重要意义．本文在实验室条件下使用仿真方法，生成飞行器的外部静态地磁环境，作用于飞行器，用安装于飞行器内部的光泵磁强计和三轴磁通门磁强计同步采集飞行器背景磁场数据，据此求解出飞行器磁干扰补偿模型的剩磁和感磁参数．由于该方法可以模拟任意地点的地磁场数据，同时能模拟飞行器在地磁坐标中的任意方向．因此，该方法具有全球适应性，模型稳定性高，样本数据测量过程无需移动飞行器载体，模型求解速度快、效率高等优点．

1 三轴地磁矢量的模拟方法

根据Tolles－Lawson方程，飞行器背景总干扰磁场可表示成［2－3］

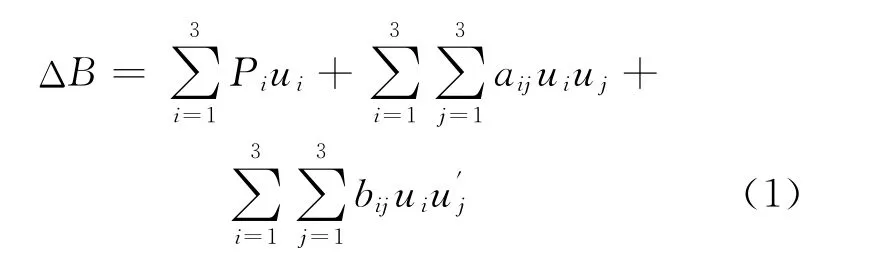
式 中：u1＝

Pi为剩磁参数；aij为感磁参数；bij为涡流磁场参数．

为了求解上式中的模型参数，需要模拟飞行器在地磁场运动时所经历的外部磁场环境，使飞行器在地磁环境磁化产生飞行器背景干扰磁场的数据样本，并由式（1）生成关于模型参数的回归方程组，进而解出模型参数．

首先讨论三轴地磁矢量的模拟方法，见图1，采用三轴正交放置的线圈，通过计算机控制线圈驱动电流来产生三轴磁场矢量［4－5］．由于三轴线圈存在安装误差，不是严格正交放置，因此产生的磁场矢量的3个分量，不仅与对应线圈的驱动电流有关，而且与其他两个线圈的驱动电流有关．为了描述磁场矢量与驱动电流的关系，对线圈的放置作如下限制：（1）z′轴线圈沿垂直方向放置，磁场向下为正；（2）x′轴线圈沿南北方向放置，磁场向北为正；（3）y′轴线圈沿东西方向放置，磁场向东为正．

图1 正交三轴线圈示意图

由于线圈安置的误差，线圈轴线x′，y′，z′不能构成正交坐标系，故建立直角坐标系xyz如图2所示：（1）坐标z轴与z′轴线圈的轴线重合，向下为正；（2）坐标y轴与z′轴线圈和y′轴线圈的轴线共面，y轴向东为正；（3）坐标x轴垂直于y轴和z轴．因而也垂直于y′轴线圈轴线和z′轴线圈轴线，x轴向北为正．

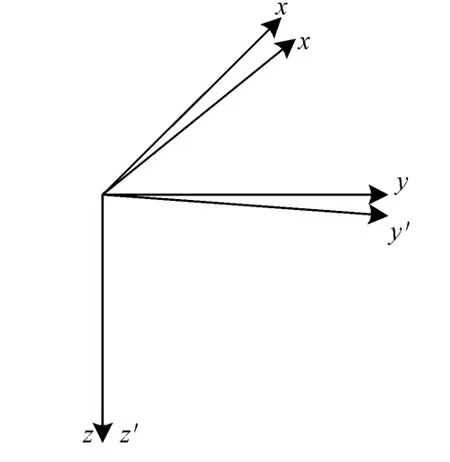
图2 计算坐标示意图

在上述计算坐标系中，磁场强度的三分量与各轴线圈驱动电流的关系如下．

称aij为三轴线圈的电磁系数．Hxo，Hyo，Hzo为本地地磁场在计算坐标系上的投影三分量．线圈电流系数和本地地磁场分量均可以预先精确求出．

为了精确模拟磁场矢量（Hx，Hy，Hz），对式（2）作线性变换如下．

式中：

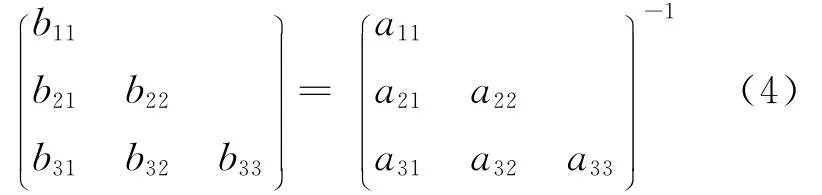
式（3）描述了线圈驱动电流 （I′x，I′y，I′z）与待模拟磁场（Hx，Hy，Hz）的对应关系．据此，可以根据所要模拟的磁场精确确定线圈驱动电流．

2 飞行器外部静态磁环境模拟

为了求解飞行器干扰磁场的模型参数，应使飞行器壳体在地磁场中受地球磁场磁化，通过测量磁化产生的磁干扰数值，建立模型参数的回归方程组，从而解出模型参数．从飞行器磁干扰模型的形式可以看出，建立回归方程组最简单的方法是不改变飞行地点，而改变飞行器相对于地磁场矢量的方向．

将飞行器安放在三轴线圈产生器的磁场均匀区中部，飞行器水平放置，头部朝北，飞行器载体坐标系与磁场线圈的计算坐标系相同．

在载体坐标系中，所模拟固定点地磁矢量为

其中：－900≤θ≤900，00≤φ≤3600．式中：H为地磁场总强度，θ为相关于载体坐标系的磁倾角，φ为磁偏角．固定H值，改变θ和φ值，可以模拟飞行器在不同飞行姿态下受地磁场磁化的结果．

为了使模型参数的求解结果稳定，θ，φ样本的选取应在其取值范围内均匀分布，但考虑到用于检测飞行器磁化状态的光泵磁强计存在测量盲区，与被测磁场矢量的夹角不能太小，也不能接近垂直．将光泵磁强计的光轴竖直取向，则要求，

式中：θi，φj任意组合，构成48个样本数据［θi，φj］，再由式（5）计算得到48组磁场矢量样本数据．

令：N ＝6 M ＝8；记：k＝ （i－1）N＋j

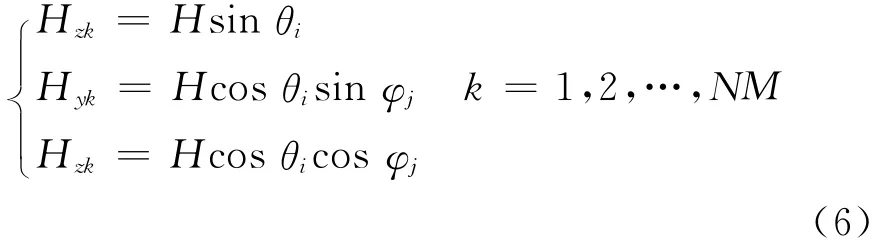
由式（6）的磁场样本数据，利用式（3）可获取相应的三轴线圈驱动电流如下：

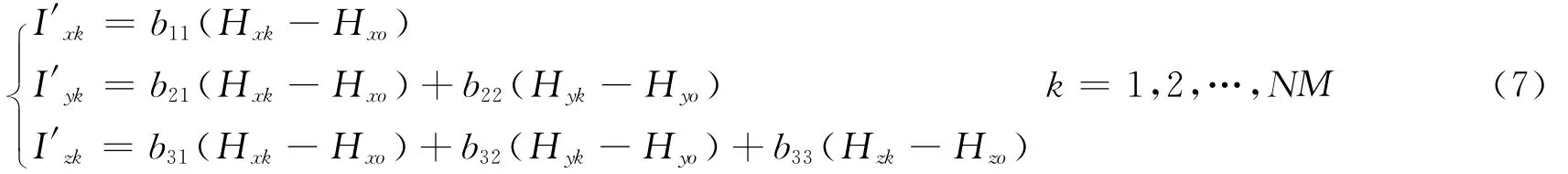
给三轴线圈加驱动电流 （I′xk，I′yk，I′zk），产生模拟磁场（Hxk，Hyk，Hzk）作用于飞行器壳体，产生飞行器在不同模拟姿态条件下的内部总磁场，使用光泵测出其大小．

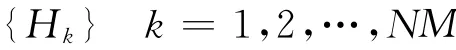
此时飞行器壳体的背景磁场可表示如下：

式中：Δhk为进行k次样本试验时的日变修正量，可使用另一台光泵磁强计在一定距离外的参考测量点测量得到．

3 剩磁参数和感磁参数求解

3．1 模型系数方程

进行磁化试验时，所加的磁场是静态磁场，所以，产生的飞行器背景磁场中只有剩磁和感磁两部分．因此有

式中：

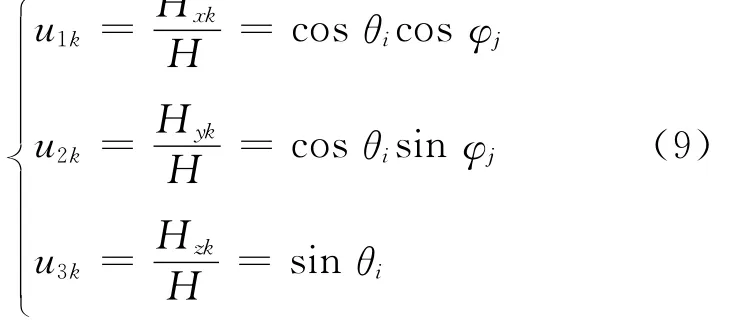
为地磁场方向余弦的样本值；pi，i＝1，2，3为模型的剩磁系数；aij＝aji，a33＝0，i，j＝1，2，3为模型感磁系数．模型式（8）中有8个独立变量．

在飞行器地磁导航应用领域，对磁场的测量精度要求不是很高，为1nT～10nT量级，而此时涡流磁场一般在1nT以下，此时忽略涡流磁场不会带来太大误差［7］．

3．2 模型定解条件

为了稳定求出模型的剩磁和感磁系数，必须有足够的测量样本数N×M，而且这些样本必须满足反映出地磁场从X，Y和Z3个方向对飞行器磁化的信息，从定解最低要求出发，至少应选择磁倾角θj的两个样本，和磁方位角φj的四个样本，构成8个样本数据，但为了提高解的稳定性，样本数可应选为独立变量数的5～10倍，从而求解感磁和剩磁参数．一般情况下式（8）构成超定方程，可以用线性回归方法求解．

4 仿真试验结果与分析

根据飞行器磁干扰补偿模型仿真试验求解的算法仿真思路，首先设定飞行器磁干扰补偿模型参数，用于模拟飞行器受地磁场磁化的规律，然后设定地磁场倾角和磁航向角，模拟飞行器的静态磁环境，再由模型生成飞行器在静态条件下的背景磁干扰数据，利用飞行器在静态条件下的背景磁干扰数据求解出飞行器磁干扰补偿模型的剩磁和感磁系数．

根据飞行器背景磁干扰的仿真数据样本，对飞行器磁干扰模型参数进行求解，参数求解的结果及与真值对比如表1所列．

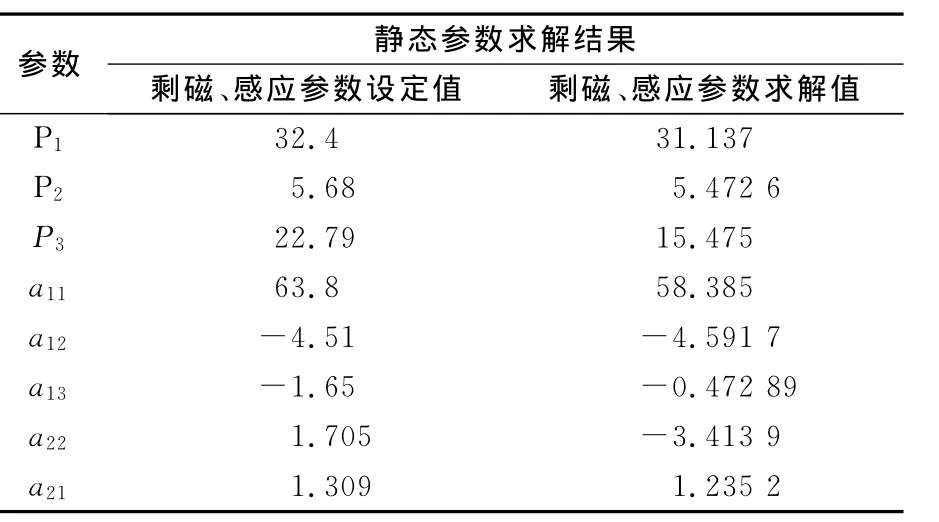
表1 模型参数求解结果

上述参数求解结果与参数设定值对比表明，算法的稳定性和精度良好，模型的偏差不超过10%．

5 结束语

为了能够满足飞行器的快速反应要求，本文在仿真试验条件下对飞行器外部静态磁环境进行模拟，通过计算机控制正交放置的三轴线圈驱动电流产生磁干扰数值，建立模型参数的回归方程组，从而解出飞行器磁干扰模型中的剩磁和感磁参数，仿真试验结果表明，飞行器外部静态磁场的模拟精度较高，模型的偏差不超过10%，剩磁和感磁参数的求解精度和稳定性良好，能够满足飞行器的快速反应要求．

［1］邓 鹏．谭 斌，林春生．飞行器外部磁场干扰补偿的预处理［J］．海军工程大学学报，2011，23（3）：58－61．

［2］谭 斌，林春生，张 宁，等．地磁场梯变对飞机磁场求解径度的影响分析［J］．武汉大学学报：信息科学版，2011，36（12）：1482－1485．

［3］谭 斌，林春生，还迎春．地磁场水平梯度对飞机磁场干扰补偿径度的影响［J］．海军工程大学学报，2012，24（6）：75－79．

［4］黎敏谦，陈菊秋，李 雪．三轴线圈磁体模拟产生舰船磁场的方法［J］．舰船电子工程，2011，31（1）：156－159．

［5］许 淼．三轴磁场模拟装置的设计［D］．上海：上海交通大学，2012．

［6］袁杨辉．地磁导航中地磁变化场的研究［D］．武汉：华中科技大学，2012．

［7］庞学亮，王 清．高速飞行器背景磁场模型分析与改进［J］．四川兵工学报，2010，31（5）：22－24．