智能积分器在船载大口径天线伺服系统中的应用

丁求启，陶 敏，张桂平

（中国卫星海上测控部 江苏 江阴 214431）

天线伺服系统是一个单输入单输出控制系统，所以目前国内绝大多数天线伺服系统的控制器均采用PID控制器。船载雷达天线伺服系统控制部分由3个环路组成：电流环、速度环及位置环，在每个环路中均采用PID控制器[1]。将功放、电流环和速度环设计成为调速系统一体机，作为伺服系统的一个集成单元，其中的电流环PID、速度环PID控制器的参数整定后，基本保持上保持不变。位置环的PI控制器的参数在伺服系统的不同工作方式和不同的跟踪带宽下分别整定，经整定后即是确定的，保存在计算机中。在实际使用中，伺服系统根据收到指令，选择相应的参数。校正参数的检验，通常采用阶跃响应和正弦信号的频率响应。但是伺服系统跟踪的目标可能是静止的也可能是机动的目标，而且机动目标的轨迹是未知的，所以采用统一、确定的PI算法不是非常恰当。现在随着精密测量雷达的测量精度的提高、作用距离的增加以及多目标测量的要求，更多地采用大口径的雷达天线，它们的转动惯量非常大，采用常规的线性PI算法，由于积分作用的影响，伺服系统的输出响应易产生较大的超调和振荡，造成对传动链较大的冲击，不利于雷达设备的安全[2]。所以，应该根据目标的运动特性、伺服系统的误差以及误差的变化趋势，采用智能型的PI算法，适时削弱积分作用，以减小雷达伺服系统在截获目标时的超调量和振荡次数；同时在伺服系统稳定跟踪目标后恢复或加强积分作用，以保证伺服系统的跟踪精度。

文中以新测量船天线伺服系统作为研究对象，将智能积分与传统的PID算法相结合应用到测量船伺服系统跟踪回路中，以达到提高伺服系统性能的目的。

1 PID算法简述

PID控制系统原理如图1所示。

图1 PID控制原理图Fig.1 Diagram of PID control

PID控制以其简单可靠、鲁棒性较强容易实现以及稳定无静差等优点而普遍应用于实际工业工程[3]。为了用计算机对其进行计算，把连续形式的微分方程转化为离散形式的差分方程。离散PID控制规律为：

式中：u（k）为采样时刻k时的输出值；

e（k）为采样时刻k时的偏差值；

u（k－1）为采样时刻 k－1 时的偏差值。

式（1）中的输出量为全量输出，它对应于电机每次应到达的绝对量，这就是PID控制规律的离散化形式。

按式（1）计算时，u（k）输出值与过去所有状态有关。计算机需记忆从初始状态开始的所有值，这将占用大量的内存和浪费大量的时间，甚至无法实现。在工程实践中一般采用增量式算法。

根据式（1），写出 k－1采样时刻的输出值

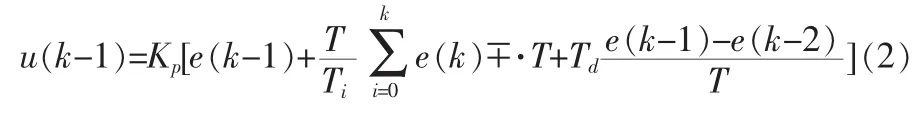
用式（1）减去式（2）得

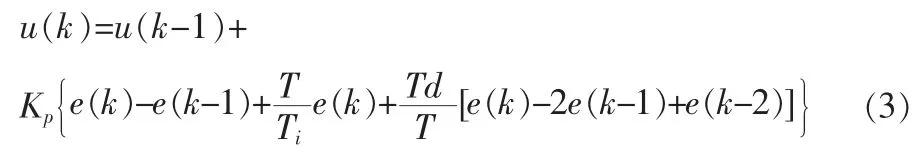
此式即为PID全量控制算式的递推形式，它在计算时刻的输出量 u（k）时，只需使用 k时刻的偏差 e（k），以及前两次的偏差值 e（k－1），e（k－2）和前一次的输出值 u（k－1），可节省内存空间和计算时间。

2 智能积分器

早在20世纪80年代，专家们就从常规PID控制中得到启发，将仿人智能应用到改进PID控制中，所产生的仿人智能控制算法有效地利用了积分的控制手段，按照人的思维，根据控制系统的动态变化进行计算机处理后，控制系统品质明显改善。与常规PID相比，仿人智能积分控制具有响应速度快、超调小，甚至没有超调等优点[4]。

这种积分器的数学模型为下式：

式中：ei（t）为积分器的输入信号；

e˙i（t）为积分器输入信号的变化率；

e0（t）为积分器的输出信号；

τ为积分器的时间常数；

tm为 ei（tm）=0 的时刻，m=0，1，2……；

tm+1 为e˙i（tm+1）=0 的时刻，m=0，1，2……。

式（4）表示：当控制系统的误差绝对值的变化率|ei|′≥0，即控制系统的误差朝着继续增大的方向发展时，我们让这个积分器真正起积分作用，以抑制误差继续增大；反之，当控制系统的误差绝对值的变化率|ei|′＜0，即控制系统的误差朝着继续减小的方向发展时，则让这个积分器变成保持器，保持e0（tm+1）等于常数，仅起一个放大器的作用；而当 e0（tm）=0 时，我们赋予这个积分器一个遗忘因子的职能，以消除过去的积分值，或信号的保持值，让控制系统保持在零误差状态。可见这种积分器一身具有3种功能：积分器、保持器（或称放大器）和遗忘因子的功能。它会根据控制系统的实时误差，以及误差的发展趋势，自动地确定积分器的控制功能。在阶跃信号输入下，它的实时控制功能如图2所示。

图2 智能积分器的实时控制功能Fig.2 Real-Time control curve of Intelligent Integrator

图中，C（t）为控制系统的输出；ei（t）为控制系统的误差信号，也是积分器的输入信号；在 Ai（i=1，2，3，…）时域内，该积分器完成式中保持器的功能；在 Bj（j=1，2，3，…）时域内，实现式中的积分器功能；在 t=tm（m=1，2，3，…）的时刻，ei（tm）=0 即完成式中的遗忘因子功能。

智能积分器不仅相位滞后比线性积分器超前23°～62.4°，利于增加伺服系统的相位裕度、提高伺服系统的稳定性；而且智能积分器幅值随误差信号级数阶次增加而衰减的特性，也使得伺服系统在将要产生振荡时，其系统增益自动降低，以抑制伺服系统的振荡、减小或消除伺服系统的超调。或者在相同的相位、幅值裕度条件下，伺服系统采用智能积分器，可以加快伺服系统的响应速度、提高伺服系统的跟踪带宽[5]。

3 船载雷达伺服系统的模型

新测量船伺服控制系统的基本原理是负反馈的闭环控制系统，基本的环路是位置控制，位置环内还含有速度环，速度环内还包含有电流环，控制对象是天线和传动机构，如图3所示。

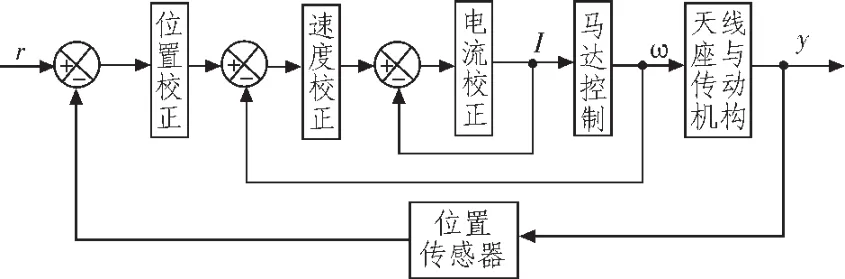
图3 伺服系统控制环路Fig.3 Diagram of servo control loop

它有3层反馈，从外环看，就具备有给定、反馈、比较、校正、执行结构等5个环节。至于内部的两层环路是为了达到一定的技术性能而设置的，可以把它们归入校正环节。设置电流环的目的是为了改造速度环控制对象特性，为速度环校正创造方便条件；设置速度环的目的是为位置环提供良好的控制对象，使之便于校正。位置环是由计算机完成闭环校正运算，它根据跟踪接收机、微光电视自动跟踪、数字引导、手动控制等位置回路不同工作方式，分别进行位置校正运算，并将运算结果送给速度回路[6]。

船载雷达伺服系统模型如图4所示。

图4 船载雷达伺服系统模型Fig.4 Mathematical model of the radar servo system of Ship-borne

船载测量雷达的波束范围很窄，而雷达接收机的线性范围就更窄。所以在一个小的误差范围内，通常将雷达伺服系统作为一个线性定常系统来考虑。所以F1定义了误差信号的线性范围，而F2则定义了位置环PI控制器输出的线性范围。

G1是位置环PI调节器模型；G2是速度环等效模型，其最大输入uimax=±10 V，电机轴最高输出转速ωmax=2 000 rpm，故速度环闭环增益K为：

G3是传动链的传递函数，因为天线最大转速为30°/s，所以传动链的速比为：

G4是传动链柔性造成的等效二阶振荡环节的传递函数，其模型为：

其中，ξ为阻尼系统；ωL为结构谐振频率，它与传动链的刚度KL和天线负载的转惯量动JL有关：

阻尼系数 ξ=0.1，结构谐振频率 ωL=20 rad/s≈3.18 Hz。 低的ξ和ωL对雷达伺服系统的动态性能有很大的影响。

伺服系统的主要技术指标为位置环带宽fB=1 Hz、加速度误差常数Ka=4，目前船载伺服系统位置环使用的校正环节G1（s）为：

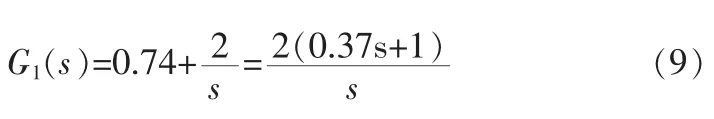
4 智能积分器的应用

式（4）所示的智能积分器具有3种功能：积分、保持和清零（遗忘因子），它根据误差和误差变化率的大小和符号在这3种功能之间自动切换；而如式（9）所示的线性积分只有在伺服系统的误差极性变化后，积分器的输出才能逐渐清零、进而反向积分。

对式（4）和式（9）所示的二种积分器构成的伺服系统分别进行仿真，其输入信号均为 θi（t）=2u（t），其中 u（t）是单位阶跃信号。比较图5和图6的动态品质，结果如表1所示。智能积分器由于在误差“归零”的过程中，采取保持器策略，“归零”速度不及普通积分器，所以其上升时间较长；因为保持器策略，在误差接近零时，智能积分器的输出较小，同时在误差过零时，具有“遗忘”功能，所以超调量由普通积分器的37%下降到4%，因而过渡过程时间也大大缩短。

图5 普通积分器单位阶跃响应曲线Fig.5 Unit step response curve of PID integrator

图6 智能积分器单位阶跃响应曲线Fig.6 Unit step response curve of intelligent integrator

表1 动态品质比较Tab.1 Dynamic quality between PID and intelligent integrator

船载雷达系统由于跟踪精度要求高、波束宽度窄，所以一般在搜索和截获目标时，需要目标的理论轨迹或其它设备引导，而且是在较远的距离上进行目标的搜索和截获，这时由于目标和雷达的相对位置关系，目标相对雷达天线方位、俯仰角的速度较小。所以式（4）的智能PI调节器，因其到达平衡位置时的超调量小，比较适用于伺服系统对目标的截获过程，尤其是对于船载大口径、大惯量的雷达天线。

5 结 论

文中通过对新测量船伺服控制系统的分析，建立了伺服系统的控制模型，并将智能积分器应用到位置控制环路中。仿真结果表明，智能积分器能够有效的减小超调量，加快调节速度，取得了较好的控制效果。

[1]瞿元新．航天测量船测控通信设备船摇稳定技术[M]．北京：国防工业出版社，2009．

[2]赵刚，朱伟．模型PID控制在伺服系统中的应用[J]．制作业自动化，2009，31（10）：180-182．ZHAO Gang，ZHU Wei.Application of fuzzy-PID control technology in servo system design[J].Manufacturing Automation，2009，31（10）:180-182.

[3]吴麒．控制系统的智能设计[M]．北京：机械工业出版社，2003．

[4]许春山，郭毓，曹广益．一种变参数PID控制器在浇注机器人伺服系统中的应用[J]．机器人，2001，23（7）：676－681．XU Chun-shan，GUO Yu，CAO Guang-yi.A kind of VAPID control used in the servo system of pouring robot[J].Robot，2001，23（7）:676－681.

[5]万其，邵兵，胡芳芳．雷达伺服系统中非线性控制技术研究[J]．现代雷达，2010，32（8）：71－73．WAN Ji，SHAO Bing，HU Fang-fang.A study on non-linear control technology in radar servo system[J].Modern Radar，2010，32（8）:71－73.

[6]傅成华，谭飞．一种新型智能积分器的设计与分析[J]．四川轻化工学院学报，2004，17（18）：28－32．FU Cheng-hua，TAN Fei.Design and analysis of a new intelligent integrator[J].Journal of Sichuan Institute of Light Industry and Chemical Technology，2004，17（18）:28－32.