各向异性对InAs/GaAs量子点应变分布的影响

汤乃云

(上海电力学院电子与信息工程学院，上海 200090)

半导体量子点的三维量子效应［1-4］，使电子运动的自由度降低，导致体系的有效状态密度和电子的能量发生显著变化，表现出一系列新颖的物理特性，如量子隧穿、库仑阻塞、非线性光学效应等［5-7］.由于InAs/GaAs量子点的晶格失配较大，使得应变效应在其S-K生长模式中起主导作用.同时，在量子点结构中的应变效应改变了电子能带结构，强烈影响着量子点光电器件的性能［8］.因此，了解这种应变场性质对于计算量子点内部电子能级、构造量子点器件是至关重要的［9，10］.

计算量子点内部应变场需要解决具有一定形状的量子点的三维弹性理论问题，其一般方法为有限元法和原子力学方法［11，12］，但这些数值方法都需要进行大量繁琐的计算;而格林函数法作为一种分析方法，可以快速地计算各种形状量子点的应变分布［13］，且非常适合作为计算量子点电子性质的输入部分.

1 格林函数方法

格林函数代表一个点源在一定的边界条件和初始条件下所产生的场.根据点源的场，利用叠加的方法就可以计算出任意源所产生的场.

引入格林张量Gln(r)代表作用在原点上的一个n方向的单位力引起坐标r在l方向上的位移，对于无限大、各向异性的弹性介质，格林张量元的解为:

式中:r——空间坐标，r=(x1，x2，x3)，当→∞时，Gln(r)→0;

λiklm——弹性模量的张量元.

为了求解方程(1)，对其进行傅里叶变换，得到线性方程:

单个量子点的广义位移可以由格林张量和量子点表面分布的应力的卷积来表达:

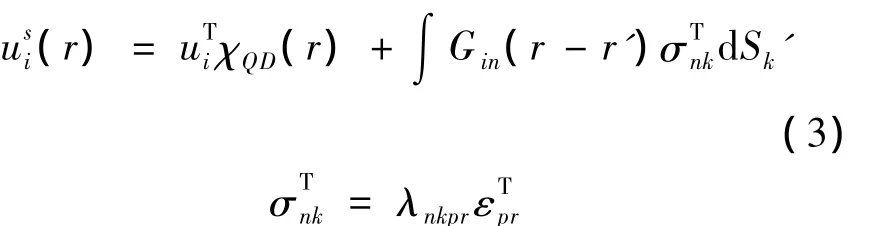
式中:χQD(r)——量子点的特征函数，在量子点内其值为1，在量子点外其值为0;

s——单个量子点.

由弹性力学定义，有:

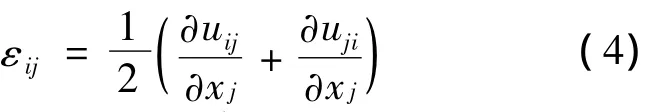
方程(3)的积分分布在整个量子点的表面，根据高斯理论和式(4)，可以得出单个量子点结构的应变张量为:

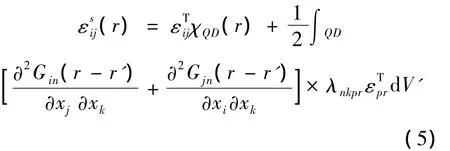
式(5)中的积分包含整个量子点，根据卷积理论，采用傅里叶变换，得到:

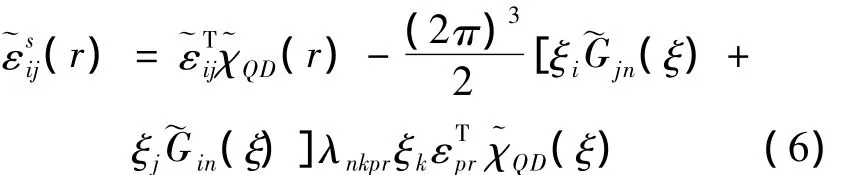
方程(6)给出了任意形状单个量子点的应变张量的傅里叶变换普遍表达式，量子点的不同形状在其中仅仅作为特征函数的傅里叶变换出现.

量子点阵列的应变场可以由单个量子点的应变场叠加得到:

式中:d1，d2，d3——x，y，z 方向量子点阵列的周期.

对于εij，必须满足周期性量子点阵列弹性能量的最低要求，也就是对于整个3D超晶格原胞，应变张量的平均值=0.根据式(7)得出，εij的傅里叶变换多项式系数为(2π)3/(d1d2d3)(ξn)，其中 ξn=(2π)(n1/d1，n2/d2，n3/d3).因此，量子点阵列的应变张量为:

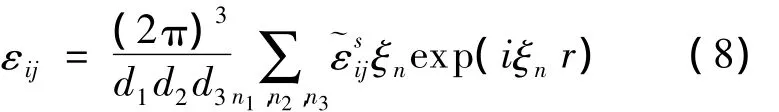
除了n1=n2=n3=0的情况外，对所有n1，n2，n3展开积分.对于立方对称的量子点，弹性模量具有3个独立分量:

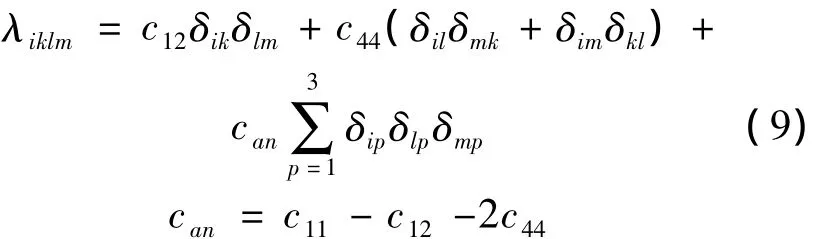
式中:c11，c12，c44——弹性模量;

can——描述张量中各向异性的部分.

如果各向同性，则can=0，且弹性模量适用于各向同性的Lame常数，此时c12=λ，c44=μ.

经过一系列变换后，对于立方对称的量子点，其应变张量的傅里叶变换形式为:

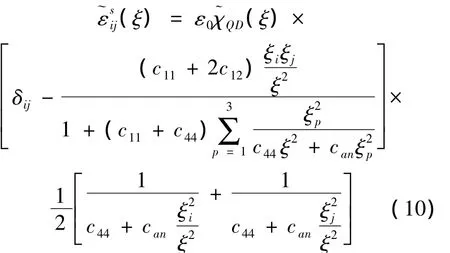
式(9)和式(10)给出了任意形状量子点的应变张量的傅里叶变换形式.量子点的形状在式(10)中只表现为量子点特征函数的傅里叶变换.对于量子点特征函数的傅里叶变换，可表示为:

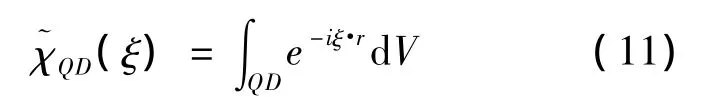
对于球形量子点:

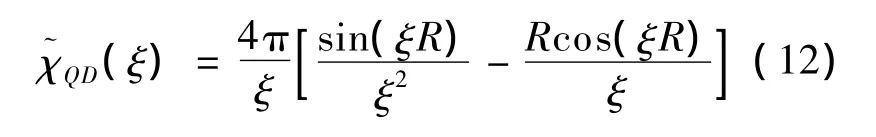
对于立方体量子点:

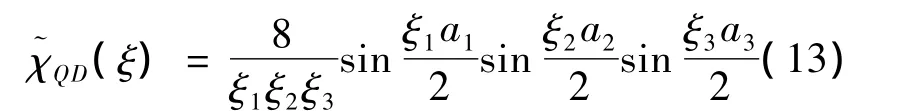
对于金字塔量子点:

式中:R——球的半径;

a1，a2，a3——立方体的边长;

Lx，Ly，h——金字塔的两个底边长和高度.

对于透镜型量子点:

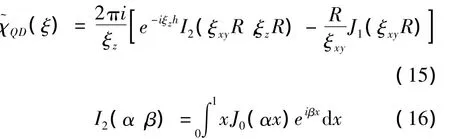
式中:R——透镜基底半底;

h——高度;

J1——贝塞尔函数.

2 影响量子点应变分布的因素

量子点中的应变分布由3个物理因素决定.一是量子点形状的各向异性.由于目前实现生长的InAs/GaAs量子点具有不同的形状和对称程度，这也决定了它们内部的应变不同，从而影响了其能带结构.二是量子点的弹性性质的各向异性.对于立方晶体，弹性各向异性的程度用弹性张量的各向异性部分can=c11-c12-2c44来描述.如果can=0，就简化为各向同性的近似;如果其大小与其他弹性模量近似，弹性性质就表现为强烈的各向异性.由于Ⅲ-Ⅴ族半导体化合物弹性张量的各向异性部分～c12～c44，因此其各向异性程度很强［14］.三是量子点的尺寸和体积.

由于流体静压应变ehh=εxx+εyy+εzz和单轴应变eb=εzz-(εxx+εyy)/2分别决定了量子点内电子能级和轻、重空穴能级及其相互分裂，因此在下面的计算中，主要关注这两个应变分量.在失配应变弛豫之前，所有材料都具有相同的晶格距离，因此计算InAs/GaAs量子点中的应变时，采用了GaAs材料的弹性常数:ε0=-0.067，c11=1.18 ×1011Pa，c12=5.4 ×1010Pa，c44=5.9 × 1010Pa.所有量子点的生长方向均为(001)方向，且各向同性介质can=0 Pa，各向异性介质can=-0.54×1011Pa.

2.1 量子点形状

图1为在弹性性质各向异性模型下球形(sphere)和立方体(cubic)量子点在(001)，(101)，(111)3个方向的应变.其中球形量子点的半径r=4 nm，立方体量子点的边长a=8 nm.

由图1可以看出，在不同形状的量子点内，其流体静压应变大小几乎相同，这说明量子点形状对流体静压应变的影响极少.由于这两种量子点在(101)和(111)方向的尺寸大小不同，因此流体静压应变由负值变为零的位置也不相同.而对于单轴应变，在(001)和(101)方向的量子点内，立方体量子点的单轴应变大于球形量子点，在量子点外，立方体量子点具有较小的单轴应变.在(111)方向，两种结构量子点的单轴应变均为零.

图1 球形和立方形量子点的流体静压应变ehh和单轴应变eb沿选定方向的变化曲线

2.2 弹性张量的各向异性

目前，量子点的形状主要有球形、立方形、透镜形及金字塔形.其中，透镜形和金字塔形量子点在实验生长时最为常见，且它们的结构对称度较低，其流体静压和单轴应变对形状的依赖则更为复杂.

根据各向同性和各向异性模型，图2给出了金字塔形量子点的流体静压应变和单轴应变在(001)，(101)，(111)3个方向的变化曲线.

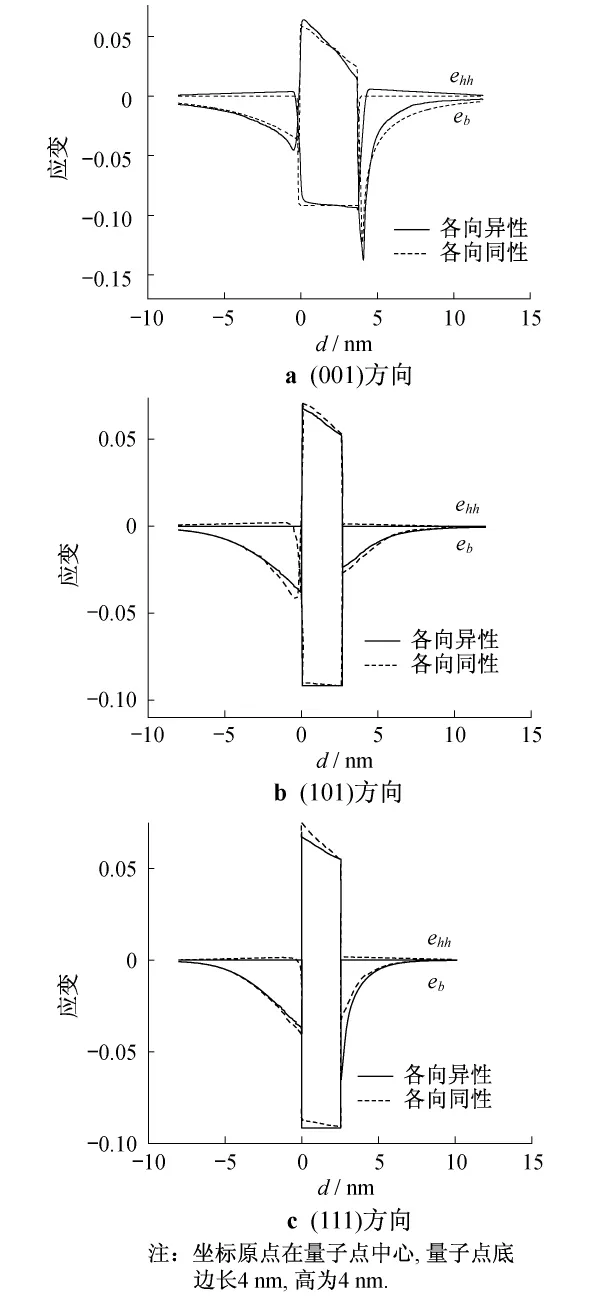
图2 金字塔形量子点的流体静压应变ehh和单轴压变eb沿选定方向的变化曲线

由图2a可以看出，由于金字塔量子点形状有个尖锐的顶角，因此其单轴应变在(001)方向呈陡峭变化，并且具有一个极小值.与此相似，在图2c中(111)方向量子点的界面处，可以看到单轴应变的尖锐变化，并处于极值.但由于(111)方向量子点界面的形状变化不如(001)方向明显，故该处应变变化不如图2a中的尖锐.由此可知，当量子点形状有陡峭变化(即具有尖点或边界)时，其单轴应变存在尖锐变化，并且处于极值状态.

由图2b中可以看出，对于各向同性模型，流体静压应变为常数，即在量子点内ehh=-0.092，在量子点外ehh=0.对于各向异性模型，ehh随空间变化，由量子点中心至量子点顶端逐渐变大，但变化量较小，仅增大了-0.006.因此，即使考虑了量子点弹性张量的空间各向异性，其流体静压应变受空间变化的影响也较小.

对于金字塔形量子点，其弹性性质的立方对称度大于量子点形状的对称度，因此应变分布中的各向异性主要由量子点形状的各向异性决定.由图2b可以看出，在量子点内外，弹性性质的各向同性和各向异性模型的结果都给出了相似的应变值.弹性性质的各向异性引起的流体静压应变和单轴应变的变化量均小于10%，弹性性质的各向异性对于量子点应变分布的影响较小.因此，在计算量子点能级时，完全可以采用弹性张量的各向同性模型.

2.3 量子点的尺寸和体积

保持Q值一定，在弹性张量的各向异性模型下，图3给出了金字塔形量子点的流体静压应变和单轴应变沿(001)方向随体积变化的曲线.

图3 金字塔形量子点流体静压应变和单轴应变沿(001)方向随体积变化的曲线

由图3可以看出，当量子点高度分别为2 nm，4 nm，6 nm时，量子点的流体静压应变没有变化，仅单轴应变在量子点尖顶处存在微小变化.因此，当Q不变时，量子点体积的变化对其应变分布几乎没有影响.此结论对于弹性张量的各向异性模型同样成立.

在保持量子点高度h=4 nm不变时，图4给出了金字塔形量子点在不同的Q值下沿(001)方向的应变分布曲线.

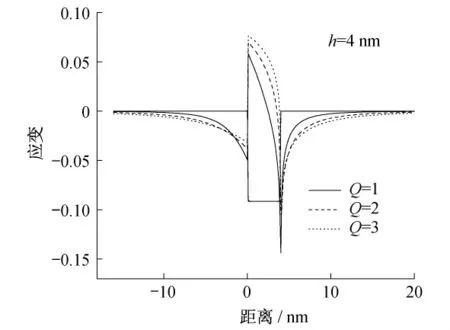
图4 在不同Q值下金字塔形量子点流体静压应变和单轴应变沿(001)方向的变化曲线

由图4可知，量子点的流体静压应变在不同的Q值下均为常数，而单轴应变受Q值影响较大.当Q=1时，单轴应变在其2/3高度处变为负值，这说明该点处εzz=εxx=εyy，量子点中存在纯粹的流体静压应变.由于单轴应变符号的改变，量子点的重空穴能级开始低于其轻空穴能级.对于较大的Q值，这种转变的发生更靠近量子点的顶点处.当Q=2时，位于距顶点约1/10处.当Q=3时，约位于顶点处.同时，单轴应变的最大值随Q值的增大而增大，而最小值随Q值的增大而减小.

另外，由图4可以看出，当 Q值增大时，在InAs量子点周围的GaAs势垒中，其单轴应变非零区域增加，即量子点高度越低(量子点越平坦)，应变对GaAs势垒的影响越大.

相对于量子点体积保持不变时应变基本不变的情况，量子点的高度变化对应变的影响来源于GaAs基底(或势垒)对不同形状(即高度)量子点的影响.为了进一步了解量子点高度变化对应变的影响，图5给出了量子点应变分量εxx和εzz沿(001)方向的变化曲线.

在靠近量子点基底处，InAs材料平行于生长平面内的晶格常数被GaAs基底压缩，垂直于生长平面内的晶格常数被拉伸，由图5可以看出，对于不同的Q值，量子点靠近基底处的εxx为负值，εzz为正值.在靠近量子点顶点处，InAs材料平行于生长平面内的晶格常数被GaAs势垒拉伸，垂直于生长平面内的晶格常数被压缩.同时，Q值不同的量子点因其形状不同，在顶点处垂直方向受压缩程度不同.Q值较大的量子点由于其形状较为平坦，在向顶点靠近时，其晶格受势垒材料的压缩不明显，因此z方向的晶格常数仍大于未应变时的数值，εzz变为负值的趋势较为缓慢;在量子点内大部分区域，εzz为正值并与εxx的符号相反，单轴应变eb=εzz-(εxx+εyy)/2为正值;Q值越大，量子点内部单轴应变为正值的区域就越大，其符号由正变负的区域就越靠近量子点的顶点.

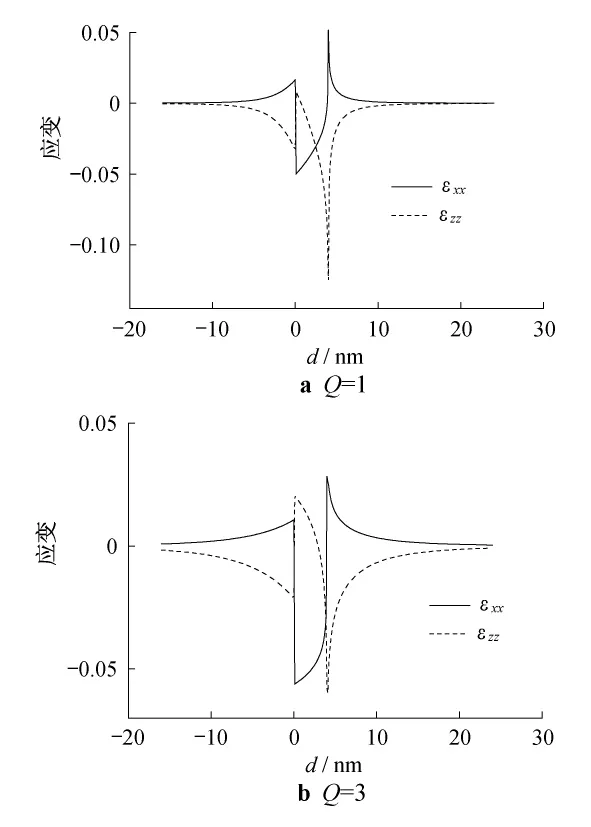
图5 量子点应变平行分量εxx和垂直分量εzz沿(001)方向的变化曲线

3 结语

相比于弹性模量的立方对称度，实验生长的量子点的形状具有更低的对称度.本文采用格林函数方法计算了自组织生长(S-K)的量子点内部的应变分布.结果表明，弹性模量的各向同性和各向异性模型都给出了非常相近的应变.因此，对于形状对称度较低的量子点，其应变分布主要是由形状的各向异性决定，而不是由弹性张量的各向异性决定.

量子点的不同形状对其流体静压应变的影响较为微弱，而对单轴应变的影响则比较复杂.当量子点保持Q值不变，仅体积发生变化时，量子点内部的应变几乎不受影响，而量子点内应变分布对其三维尺寸的相对变化较为敏感.

［1］ ARAKAI Y，SAKAKI H.Multidimensional quantum well laser and temperature dependence of its threshold current［J］.Applied Physics Letter，1982，40(11):939-941.

［2］ ASADA M，MIYAMOTO Y，SUEMATSU Y.Gain and the threshold of 3-dimensional quantum-box lasers［J］.IEEE J Quantum Electron，1986，22(9):1 915-1 921.

［3］ PANK D，TOWL E，KENNERLY S.Normal-incidence intersubband(In，Ga)As/GaAsquantum dotinfrared photodetectors［J］.Applied Physics Letter，1998(14):1 937-1 939.

［4］ MAIMON S，FINKMAN E，BAHIR G，et al.Intersublevel transitions in InAs/GaAs quantum dots infrared photodetectors［J］.Applied Physics Letter，1998(14):2 003-2 005.

［5］ GEERLINGS L J，ANDEREGG V F，HOLWEG P A M，et al.Frequency-locked turnstile device for single electrons［J］.Physical Reviwe Letters，1990，64(76):2 691-2 694.

［6］ REITZENSTEIN S，HEINDEL T，KISTNER C，et al.Forchel Low threshold electrically pumped quantum dot-micropillar lasers［J］.Applied Physics Letter，2008(6):1 104-1 107.

［7］ MIZRAHI U，REGELMANDV，GERSHONID，etal.Quantum dots:a source of multicolor photons with tunable statistics and correlated polarizations［J］.Phys Stat Solidi(b)，2003(2):297-300.

［8］ GRUNDMANN M，STIER O，BIMBERG D.InAs/GaAs pyramidal quantum dots:strain distribution，optical phonons，and electronic structure［J］.Physics Review B，1995，52(16):11 969-11 981.

［9］ O’REILLY E P.Valence band engineering in strained-layer structures［J］.Semicond Science Technology，1989，4(3):121-137.

［10］ O’REILLY E P，ADAMS A.Band-structure engineering in strained semiconductor lasers［J］.IEEE J Quantum Electron R，1994，30(2):366-379.

［11］ BENABBAS T，FRANCOIS P，ANDROUSI Y，et al.Stress relaxation in highly strained InAs/GaAs structures as studiedby finite element analysis and transmission electron microscopy［J］.Journal of Applied Physics，1996(5):2 763-2 767.

［12］ JOYCE P B，RU E C Le，KRZYZEWSKI T J，et al.Optical properties of bilayer InAs/GaAs quantum dot structures:Influence of strain and surface morphology［J］.Physical Review B，2002，66(7):5 316-5 323.

［13］ ANDREEV A D，DOWNES J R，FAUX D A，et al.Strain distributions in quantum dots of arbitrary shape［J］.Journal of Applied Physics，1999(1):297-305.

［14］ KRIJN M P C M.Heterojunction band offsets and effective masses in III-V quaternary alloys［J］.Semicond Science Technology，1991，6(1):27-31.