XK2535数控龙门铣床滑枕动态特性研究

陈水胜，徐 旭，华中平，戴 晨

（1湖北工业大学机械工程学院，湖北 武汉430068；2武汉国威重型机械制造有限公司，湖北 武汉430223）

滑枕是龙门铣床中的重要部件，机床采用主轴滑枕结构主要目的在于增强机床的动刚度，适应大型零件的强力切削［1］.其内部包含主轴、轴承、垂直铣头等重要部件与主轴箱配合的是溜板，溜板内安装有进给丝杠.进给丝杠与固定在滑枕上的螺母座连接，通过丝杠的转动来带动滑枕的伸出与回缩.所以滑枕的静刚度与动刚度影响着机床的精度与稳定性，为了使机床具有高刚度、振动小、变形小、噪声低、良好的抵抗受迫振动和自激振动能力的动态性能，有必要在加工滑枕之前对其进行分析，了解其变形情况和振动情况［2］.

1 滑枕的静态分析

1.1 滑枕模型的建立

首先采用SOLIDWORKS对滑枕进行实体建模，滑枕横截面尺寸为600mm×600mm，长度3 525mm，内部为不规则的空间几何模型，材料为QT600－3，滑枕总重量为2 700kg，材料弹性模量为1.6E11Pa，泊松比为0.29.忽略温度对滑枕变形的影响，为避免网格划分时网格尺寸相差很大而影响计算结果，简化了结构中的一些小圆角和小倒角，由于主轴对滑枕有一定力的作用，把主轴对滑枕作用力等效成均布力加载在轴承座上.

该机床可以进行铣、镗、钻、铰加工，本文以铣削加工为例，采用端铣刀逆铣，该机床主电机功率为90kW，主轴转速范围为5～1 200r／min，主轴扭矩8 000N·m，刀具材料为硬质合金，刀具主偏角为60°，前角为5°，工件材料为灰铸铁，强度极限为250 MPa，铣削深度ap＝7mm，进给量fz＝0.28mm／z，铣削速度vc＝110m／min.由铣削力的经验公式

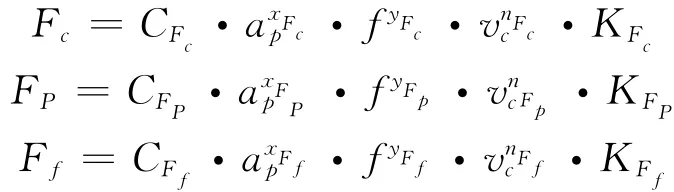
式中Fc、Fp、Ff分别为主切削力、背向力、进给力；CFc、CFp、CFf为公式中的系数，根据加工条件由实验确定；xF、yF、nF表示各因素对切削力的影响因素系数；KFc、KFp、KFf为不同加工条件对各切削分力的影响系数.

由以上公式解得主切削力Fc＝48 227N，背向力Fp＝19 290N，进给力Ff＝14 468N.此外滑枕还受到上部主轴箱的重力及螺栓的预紧力作用，则螺栓预紧力

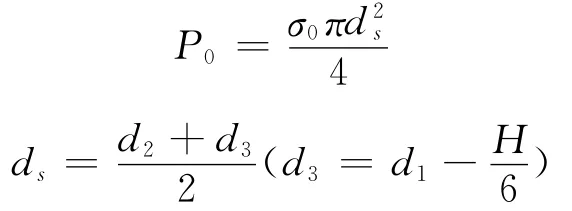
式中ds为螺纹部分危险剖面的计算直径；d2为螺纹中径，H 为螺纹公称高度；σ0＝ （0.5～0.7）σs，σs为螺栓材料屈服极限.

由此计算得到螺栓预紧力为P0＝1 410N.主轴箱与滑枕之间有八个螺栓连接，则总预紧力为11 280N.

1.2 结果分析

本文以滑枕伸出长度最大的工况为分析对象，对其进行静力分析，滑枕最长伸出距离为1 750 mm，并在距顶部为1 770mm的滑枕背部进行全约束.对模型进行自由网格划分（图1），有限元模型和分析结果见图2、图3.

从图2可以看出滑枕的应力分布不均匀，应力范围在6 449Pa～4.92MPa，且在滑枕背部螺母座处应力集中出现，这是因为滑枕背部有一个10mm的凸台，在凸台边缘出现应力集中，所以此处应适当加工一个圆角.由图2可以看出，滑枕总变形在0～46.5μm之间，最大变形出现在滑枕下部，是因为此处连接铣头等刀具，滑枕在此处受很大的切削力，以Y方向的径向力为最大，最大变形为30.6μm，从分析看出滑枕整体的静刚度很好，最大应力远小于材料的许用应力，说明滑枕还有很大的优化空间，可以适当的减小壁厚以节省用料，降低成本.

2 滑枕的动态分析

2.1 理论分析

在结构动力学问题中固有频率和主振型是动力学问题分析的基础.模态分析用于确定设计中的结构或机器部件的振动特性，即固有频率和主振型.主振型指的是该振动系统以此阶固有频率振动时各自由度之间振幅值的比例关系和一定的相位关系［3］.

由于滑枕里面安装有铣轴、镗杆等重要机构，滑枕的抗振性对轴与轴承之间的旋转精度有很大影响，如果滑枕的动态性能不好，很容易引起主轴与滑枕的共振，这样会严重影响机床的加工精度，所以有必要对滑枕进行模态分析，分析其固有频率和振型.

一般情况下，多个自由度系统的振动微分方程用矩阵表示为以下形式［3］：

式中：［M］为系统质量矩阵；［C］为系统阻尼矩阵；［K］为系统刚度矩阵；｛x｝为系统个点位移响应；｛F｝为为系统各点的激励向量.

分析无阻尼的系统的频率和振型问题就是模态分析，其微分方程的解是耦合的，互相耦合的N自由度系统方程经正交变化成为模态坐标下相互独立的N自由度系统的方程组，解耦后的第i个方程为：

式中：Ki为模态刚度；Mi为模态质量；Ci为模态阻尼；φi为模态振型.

从上式中可知，采用模态坐标后N自由度系统的响应相当于在N个模态坐标下单自由度系统的响应之和.采用归一化方法使模态质量归一，记模态质量归一化振型为Φ，即：

2.2 有限元动态分析

根据上述理论方程及数学模型，在滑枕伸出最长时，利用SOLIDWORKS对滑枕进行建模，然后导入ANSYS，除去一些不必要的圆角和倒角，忽略温度的影响，按自由网格对其进行网格划分，在滑枕伸出最长时对滑枕背部螺母座处进行全约束，对模型提取了九阶模态（表1），其中六阶模态见图4至图9.

结构的振动可以表达为各阶固有振型的线性组合，其中低阶固有振型比高阶对结构的振动影响较大，越是低阶影响越大，低阶振型对结构的动态特性起决定作用［4］.

由表1可看出，第一阶模态为49.049Hz，基本能满足中速要求，第二阶模态为67.651Hz，前两阶模态差别不大，但是三阶出现局部振型，说明滑枕下部壁厚相对较小，动刚度偏小，抗振性能降低，对机床高速加工产生不利影响.滑枕第七阶351.70 Hz、第八阶390.11Hz、第九阶422.74Hz，这几阶频率很接近，这主要是因为滑枕结构相对复杂，固有频率相对密集，因为复杂结构影响质量分布，使方程（［］K－ω2［］M）｛｝A＝0中质量矩阵［］M受到了影响，进而求解结果受到了影响，求出的固有频率比较接近.

表1 滑枕伸出最长时各阶固有频率和振型分析

当滑枕内的主轴旋转时产生的激振频率接近于滑枕的固有频率时将会产生共振，严重影响机床的动态精度.该铣床电机功率90kW，主轴转速范围在5～1 200r／min，由公式

计算可得，主轴激振频率范围为0.083～20Hz，远远低于滑枕的固有频率（计算表明：滑枕的固有频率范围在49.049～422.74Hz），可有效避免产生共振.

依以上分析，以不减小机床加工范围为前提，在原设计参数的基础上，提出如下改进措施：1）增大滑枕与溜板的接触面积，增加约束；2）滑枕内部X轴方向的加强筋由七个增加到十个；3）将滑枕两侧滑槽高度由65mm增加到70mm.当然，在实际生产中尽可能减少滑枕的悬伸长度，对于稳定加工质量也是有利的.

3 结论

1）用SOLIDWORKS对滑枕进行建模，再导入ANSYS系统分析计算，并对网格局部修正，提高了计算精度.

2）通过对滑枕的静力学分析，得出滑枕最大应力为4.92MPa，远远低于灰铸铁的强度极限，其静态安全系数高，这表明滑枕结构设计趋于保守，可进一步优化机构.

3）通过对滑枕进行模态分析，根据滑枕的前九阶固有频率和振型，分析了滑枕在各频率下的动态性能，得出的结论是：滑枕振动频率远高于主轴激振频率范围，但第一、二阶频率与后几阶频率差别很大.为此，针对原设计提出了几种改进措施对滑枕进行结构优化，通过具体实施及工程测试，机床的动态性能大大提高，满足高速、大功率切削的加工要求.

［1］ 程 渤，殷国富.龙门加工中心主轴滑枕结构有限元分析技术研究［J］.组合机床与自动化加工技术，2011，6（6）：12－13.

［2］ 向家伟，王 荣，徐晋勇，等.大型龙门铣床主轴滑枕结构有限元分析［J］.制造技术与机床，2009（9）：47－50.

［3］ 刘习军，贾启芬.工程振动理论与测试技术［M］.第四版.北京：高等教育出版社，2004：96－102.

［4］ 张 珂.陶瓷轴承电主轴的模态分析及其动态性能实验［J］.沈阳建筑大学学报：自然科学版，2008，24（3）：490－493.