基于禁忌粒子群优化的FCM聚类方法

陈晓霞，廖家平，赵熙临，谌金豆

（湖北工业大学电气与电子工程学院，湖北 武汉430068）

模糊C－均值是基于目标函数的无监督动态聚类方法，通过模糊理论对重要数据分析和建模，建立了样本属性的不确定性描述，比较客观地反映现实世界.该算法计算简单，具有比较直观的几何意义，成功地应用于模式识别、数据分析等领域.然而基于传统目标函数的FCM，采用迭代的爬山技术寻找最优解，本质上是一种局部搜索算法，存在一个致命问题：对初始值敏感，容易陷入局部极小值.随着群体智能方法的发展，将具有全局搜索能力的群智能算法和具有局部搜索能力的FCM相结合成为研究热点.文献［1］利用遗传算法对初始聚类中心进行优化并执行FCM算法，提高了收敛速度并改善了分类效果，增强了算法的鲁棒性；文献［2］提出了蚁群算法确定FCM模型初始聚类中心的方法，优化聚类效果；文献［3］提出了利用粒子群算法（PSO）全局寻优FCM最优初始聚类中心.这些方法能有效克服FCM算法固有的缺陷，但同时也带来新的问题.遗传算法和蚁群算法本身存在大量参数和复杂的操作，计算开销较大，对算法收敛速度有极大影响，特别是对大样本数据聚类时，聚类效果的改进不及收敛速度影响大，对整体算法没有很大优势.PSO算法简单，参数少，计算方便，求解快，但有容易早熟导致陷入局部最优解的问题.粒子群规模的选择和初始粒子的随机性也会影响其优化结果，因此保持粒子的多样性是必要的.将禁忌搜索引进粒子群算法，通过对粒子群算法的输出进行局部及邻域搜索，可以实现真正意义上的全局寻优.该混合优化算法既保留了PSO算法的并行处理能力，同时也充分利用了禁忌搜索算法的局部搜索能力，针对FCM模型全局最优初始聚类中心的确定及对FCM聚类准确性有极好的效果.

1 模糊C－均值算法（FCM）

模糊C均值算法是聚类分析中的一种基本划分方法，常采用误差平方和准则函数作为聚类准则，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而决定样本点的类属以达到自动对数据样本进行分类的目的.考虑一有限数据集X＝｛x1，x2，…，xn｝，是一组有n个m 维向量组成的样本集合.利用FCM聚类算法将它们分为C个子集，每个子集又可称为类，C为2到n之间的整数.对于每类，可用两个参数来描述它：一个是用于表示每个样本隶属于该类的概率uik，另一个是该类的中心点

对于FCM算法的整体过程，可用隶属度矩阵U＝ ｛uik，1≤i≤C，1≤k≤n｝来表示每一样本对各类的隶属程度；V ＝ ｛v1，v2，…，vc｝为所有类聚类中心集合.其目标函数采用的是类内加权平方和的极小值，可以表示为：

其中dik用来表示每类中样本与该类中心的距离，采用的是欧式距离表达方式.参数m是算法中隶属度矩阵模糊化指数权重，关于m的最优值的选取仍缺乏相关的理论指导，实验经验表明，［1.5，2.5］是参数m可实现FCM模糊聚类的有效区间［8］.根据FCM原理可知其过程是一个按其梯度下降的迭代过程.每次迭代都可以获得对应的uik和vi.其对应的结果如下：

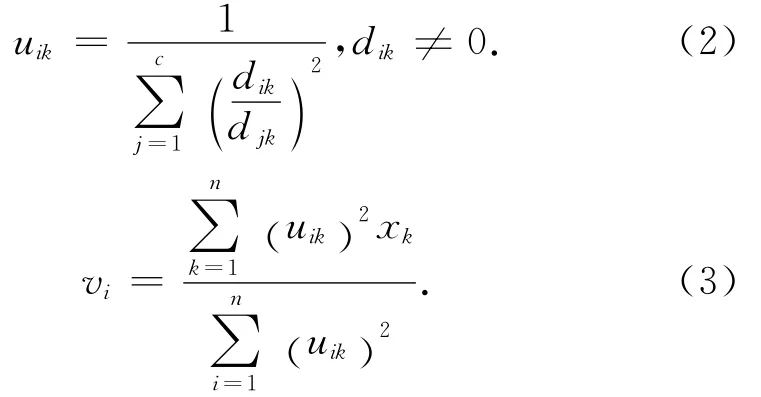
从FCM工作原理可知，该算法是敏感于初始值的.当初始值选择在某个目标函数极小点附近时，算法容易陷入该极小点所表现的聚类结果而陷入局部最优.针对该算法敏感于初始值的问题，将一些具有全局寻优能力的群体智能算法与之相结合成为研究的热点.

2 基于禁忌粒子群优化后的FCM算法

2.1 粒子群优化算法（PSO）

PSO算法是一种进化计算技术，由Eberhart博士和Kennedy博士于1995年提出.该算法是受到飞鸟集活动规律的启发，利用群体智能建立的一个简化模型.在该模型中，每个优化问题的可行解都是一个粒子Si，所有的粒子都有被优化的函数决定的适应值f（Si），每个粒子还有一个速度Vi决定他们的方向和距离，粒子们就追随当前的最优粒子在解空间进行搜索.粒子群算法具有记忆功能，只有全局最优解或局部最优解向其他粒子传递信息是个单向的信息流动，整个搜索更新过程是跟随当前最优解的过程，因此该算法较其他智能算法更快收敛最优解.它具有简单、容易实现、无须多参数调整等优点.目前广泛应用于函数优化、模糊系统控制以及其他遗传算法应用领域.该算法基本思路是：初始化一群随机解，也即是粒子.然后通过迭代找到最优解.在每次迭代过程中，粒子通过跟踪两个“极值”来更新自己，第一个是粒子本身所找到的最优解，这个解叫个体极值pBest，另一个是整个种群中找到的最优解，这个极值是全局极值gBest.经过数次迭代，直至满足停止迭代条件为止，最终得到的gBest就是要找的解.

关于PSO优化算法应考虑粒子编码、自适应函数的选择和粒子更新策略三方面内容.PSO采用的是实数编码形式，粒子的长度由优化问题决定；适应度函数的选择一般都是待优化问题的函数表达形式，在解决FCM优化问题上，一般都是将FCM的目标函数作为适应度函数，表达式如下：

标准的粒子更新策略表示如下

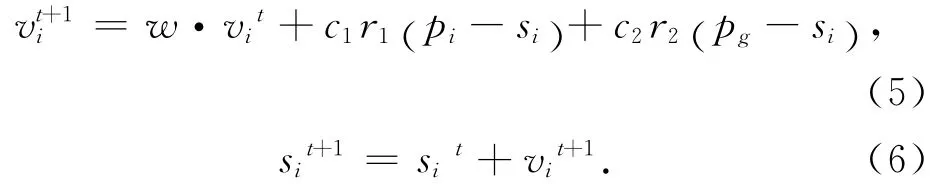
其中，参数c1和c2学习因子，r1和r2是在（0，1）区间的随机数，参数w是惯性权值，其大小决定了算法的全局搜寻能力.不同的参数选择对应的不同策略，其优化结果不同.

2.2 禁忌搜索算法

禁忌搜索算法（TS）的思想由美国工程院士科罗拉多1986年提出，是一种亚启发式搜索算法，是对局部领域搜索的扩张.禁忌算法通过引入一个灵活的存储结构和相对应的禁忌准则来避免循环搜索，同时通过藐视准则来赦免一些被禁忌的优良状态，以保证多样化的有效搜索，最终实现全局优化.TS算法在组合优化、机器学习和神经网络等领域取得很大成功.近年来，TS算法在函数全局优化方面有较多研究.

禁忌搜索算法的基本思路：TS算法从一个初始解X出发，这个初始解可以从其他启发式算法获得，也可以在可行解集合中任选.确定完初始解后，定义其对应的邻域S（x），在邻域中移动已改进当前解，从而获得新的解X′，然后从X′开始，重复搜索.在搜索过程中，要构建一定禁忌长度T的循环记忆表禁忌表，以保证算法避免循环和局部最优.同时也要遵循相应的“特赦准则”对搜索过程中最优候选解进行解禁，保证算法的顺利进行.禁忌表是个循环表，在搜索过程中仍然有可能陷入循环，因此必须给定算法停止准则以结束算法.

对于禁忌搜索算法的研究，应该把握以下几个关键点：

1）初始解的选择.TS算法必须有一个初始解，这个初始解对算法本身性能有影响.从可行解中获得初始解有一定随机性，当前更多的是将另一种启发式算法的输出作为初始解以优化算法性能；

2）禁忌长度T的选择.禁忌表长度T在很大程度上影响着搜素速度和解的质量.过大会增加计算量且易陷入局部最优；过小容易陷入循环搜索，整个搜索将围绕着相同的几个解徘徊；

3）应该遵循特赦准则.特赦准则对搜索过程中的最佳候选解进行解禁，以保证算法继续进行，是实现全局优化的关键步骤；

4）设置一个合理算法终止准则.

2.3 禁忌粒子群混合优化算法

禁忌粒子群优化算法是以粒子群算法为主体，以禁忌算法为个体在邻域中移动寻优.PSO算法输出解作为TS算法的初始解，利用TS算法在解空间搜索到更好的解，其结果相当于对粒子群的输出做更新.该混合算法既克服了PSO算法局部搜索能力较弱和存在早熟收敛的问题，又利用了禁忌搜索较强的“爬山”能力，加快了混合算法的收敛速度，提高了收敛解的有效性，实现两者优势互补.该混合算法在求解FCM最优初始中心步骤如下：

1）输入待聚类的样本数据，并设置PSO算法和TS算法中所需设置的参数，初始化粒子，t＝0；

2）计算每个粒子的适应度值，即对每个粒子Xi，根据FCM 的目标函数求出f（Ui，Xi），并找出个体极值pBest和全局极值gBest；

3）根据粒子更新策略式（5）和式（6）对每个粒子的速度和位置进行更新.

4）t＝t＋1；

5）迭代过程中若解无改进，则继续下一步，否则转为步骤2；

6）根据当前解的邻域函数产生一定数目的邻域解，进行搜索，从中选取适应度最高的若干候选解；

7）对每个候选解是否满足特赦准则进行判断，如果满足，则用满足特赦准则的最佳候选解替代当前解，并用其对应的禁忌对象替代最早进入禁忌表的禁忌对象，同时用该候选解替代TS算法的历史最优解，转入步骤6；如果不满足，则继续以下步骤；

8）判断候选解对应各对象的禁忌属性，选择候选解集中非禁忌对象对应的最佳状态替代当前解，用与之对应的禁忌对象替代最早进入禁忌表的禁忌对象元素；

9）判断是否满足终止判据条件，若为否，转为步骤2，若满足，停止迭代，输出FCM的最优初始中心.

3 实验性能测试及结果分析

为了验证禁忌粒子群优化算法提高FCM聚类收敛速度及准确率的有效性，采用VC＋＋编程对UCI数据集Iris数据集和Wine数据集进行仿真实验，将本文TSPOS＿FCM、文献［3］的PSO＿FCM 和FCM算法进行比较.Iris数据集是由150个4维向量样本组成，共分为三个种类，每个种类有50个样本；Wine数据集由178个13维向量样本组成，分为三个种类，各类样本数目分别为59、71和48.这两个数据集常用来检验聚类算法的性能.设置FCM聚类数目c＝3，模糊指标m＝2，粒子群规模N＝50，c1＝2，c2＝2，vmax＝2，vmin＝－2，最大迭代次数tmax＝100，惯性权重w＝0.729 8，最优解改变量阈值e＝1e－4，TS局部搜索半径SR＝0.3，邻域解和候选解均取8个，禁忌表长为6，记忆长度为100，局部最优解长度取4，终止判据是最大迭代次数为100或最佳值保留次数为20.表1为3个算法对2个测试数据集的实验结果，分别对3种算法做10次实验，其中FCM算法是取10实验所得最好的结果.

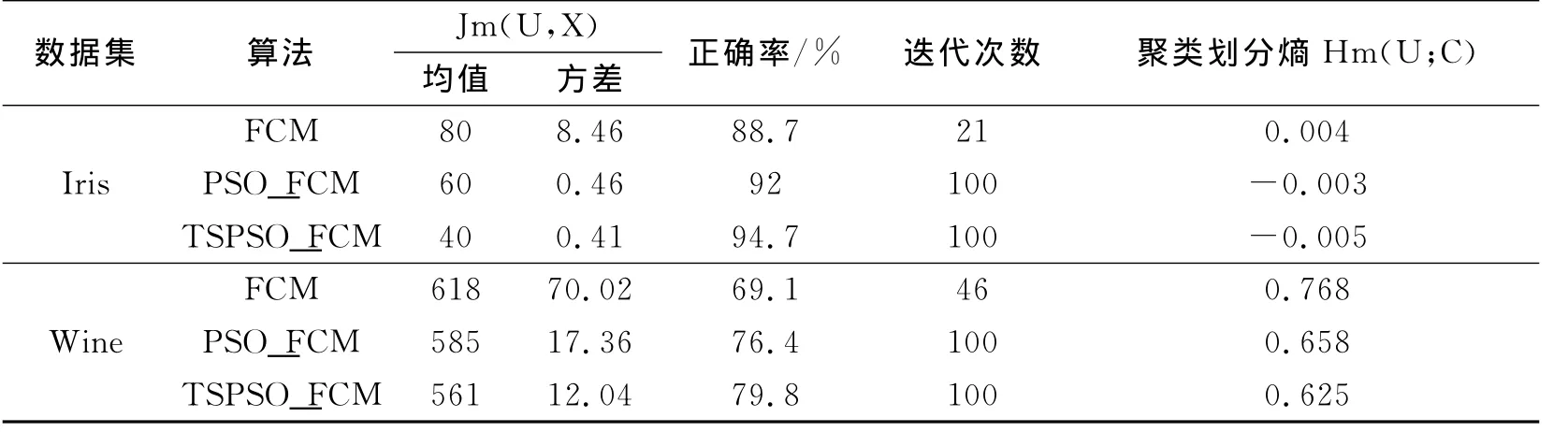
表1 各种FCM聚类算法性能比较

从表1中可以看出，TSPOS＿FCM在所有的指标上优于其他算法，其中传统的FCM算法由于采用了梯度算子，函数值下降非常迅速，容易陷入局部最小值，这是使用梯度算子很难避免的结果.而目标函数的方差较大，说明FCM的输出解不稳定，对初始聚类中心敏感.而PSO＿FCM算法中聚类正确率较高，最优解对应目标函数的方差较小，说明算法的全局搜索能力较好，算法输出最优解较为稳定.TSPSO＿FCM将禁忌算法和粒子群算法结合起来，克服了PSO后期易陷入局部最优和过于早熟问题，通过禁忌算法增加力粒子搜索空间，增加了粒子的多样性，有助于全局最优解的搜索，从评价指标上可以看出其聚类准确率是最高的，同时最优解对应方差最小，说明其最优解是最稳定的.

其中聚类划分熵Hm（U，C）是一种基于香农信息的聚类有效性函数，其表达式如下：

其值越小表示隶属度矩阵中元素接近1或0的个数越多，类别间发生混叠现象少，聚类准确率高.

4 结束语

综上所述，FCM算法存在对初始值敏感，易陷入局部极小值的缺陷，结合PSO算法能有效解决这个问题，考虑到PSO算法有可能出现早熟收敛的情况，本文引入禁忌算法增大PSO算法的搜索范围，增加粒子的多样性，同时，通过禁忌表禁忌一些局部最优解，防止陷入循环中，有效地在保证优化效果的基础上缩短了全局最优解的时间，提高了整体算法的收敛速度和聚类结果的正确率.

［1］ Chen W，Lu T.J.An improved genetic FCM clustering algorithm［C］／／2010 2ndInternational Conference on Future Computer and Communication.China，2010（1）：45－47.

［2］ 关 勤，邓赵红.改进的FCM算法［J］.计算机工程与应用，2011，47（10）：27－31.

［3］ 陈寿文，李明东.一种混合均值聚类算法的实现［J］.计算机工程与应用，2010，46（18）：132－134.

［4］ 况 夯，罗 军.基于遗传FCM算法的文本聚类［J］.计算机应用，2009，29（2）：558－561.

［5］ 赵小强，张守明.基于人工蜂群的模糊聚类算法［J］.兰州理工大学学报，2010，36（5）：79－83.

［6］ 江克勤，施培蓓.优化初始中心的模糊C均值算法［J］.合肥工业大学学报（自然科学版），2009，32（5）：762－765.

［7］ Wang Z.B.The study of an improved FCM clustering algorithm ［C］／／2010 2ndInternational Conference on Signal Processing Systems.China，2010，（2）：95－100.

［8］ 朱 林，王士同，邓赵红.改进模糊划分的FCM聚类算法的一般化研究［J］.计算机研究与发展，2009，46（5）：814－822.

［9］ 温重伟，李荣钧.改进的粒子群优化模糊C均值聚类算法［J］.计算机应用研究，2010，27（7）：2 520－2 522.

［10］朱文婕，吴 楠.一个改进的模糊聚类有效性指标［J］.计算机工程与应用，2011，47（5）：206－209.

［11］韩 琳，贺兴时.基于免疫粒子群优化的模糊C均值聚类算法［J］.西安工程科技学院学报，2007，3（21）：355－361.

［12］唐 俊.PSO算法原理及应用［J］.计算机技术和发展.2010，2（20）：213－216.

［13］张玉芳，薛青松，熊忠阳.基于禁忌搜索的动态粒子群算法［J］.计算机工程与应用.2008，44（24）：56－58.