流体力学在水轮机管路设计中的应用

孙 旺，曲 扬

（1.水力发电设备国家重点实验室，哈尔滨 150040；2.哈尔滨电机厂有限责任公司，哈尔滨 150040）

前言

流体力学，是研究流体的力学运动规律及其应用的学科。主要研究在各种力的作用下，流体本身的状态，以及流体和固体壁面、流体和流体间、流体与其他运动形态之间的相互作用的力学分支。在农业、工业、航天、军事及工程中具有重要的应用价值。本文主要谈一些流体力学在水轮机管路设计中的几点应用，在水轮机设计中，充分应用流体力学这门基础学科。

1 流体力学在管路压降中的应用（沿程损失和局部损失）

《流体力学》教材中，对于沿程损失[2]及局部损失[2]的定义及计算方法做了比较详细的阐述，通过雷诺数Re判别流态（层流、湍流等）后，应用相应经典公式，不难计算某段管路的水头损失。其中，较长管路以沿程损失为主，较短管路以局部损失为主。除流态外，沿程损失决定于管路长度、管路粗糙度等，局部损失决定于弯头、三通、滤水器、冷却器等外购件压力降及数量等。

我们可根据计算的水头损失（沿程损失和局部损失）、管路进出口高程差及管路出口流速及压强情况，判定管路进口所需压强。在水轮发电机组中，管路水头损失计算有很多重要应用。如，鉴于水轮机主轴密封润滑水的压力要求，通过计算确定主轴密封供水管路设置增压泵、减压阀情况。如，鉴于水轮机水导轴承进、出油管流量要求，进行油泵选型等。发电机上下导、推力头等也涉及管路水头损失计算。因此，管路水头损失计算是水轮发电机组设计中，非常重要的一环，对泵、阀等外购件的选型具有指导性意义。

另外，我们采用测管路静压的试验方法取得管路水头损失的真实数据。流体机械计算中常用能量守恒公式：

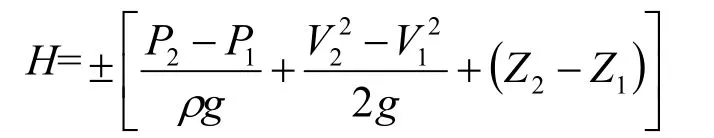
式中：下标1表示进口断面，下标2表示出口断面。在管路水头损失计算中，若按管路等径考虑，由于管路进、出口流量不变，管路内径不变，因此V2=V1。那么管路水头损失公式为：

管路水头损失的数值可由管路进出口高程及静压计算得出。值得注意的是，考虑管路进出口可能存在流态不稳等情况，管路进出口静压的测量位置应距管路进、出口有一定距离。

2 流体力学在排水管路中的应用（圆柱形外管嘴出流）

在水轮机管路设计中，部分电站的蜗壳排水管或尾水排水管需引至无压排水廊道如渗漏集水井等，如图1所示。这种情况下，我们需要计算管路出口流速，以便预期管路的振动及噪声，并采取相应的解决措施。

在不计管路沿程损失的前提下，引入圆柱形外管嘴出流流速经验公式：

若管路设计中，蜗壳排水管直接排至尾水管层的渗漏排水廊道，则h值根据机组设计不同取值会有不同，一般会在十几米以上，这样管路内水的流速会超过10m/s，远大于管路通常规定的2～5m/s。可考虑在管路中增加节流孔板或减压阀以减低管流速度。具体计算中，还可考虑管路沿程损失对降低管流速度的影响，但该影响相对较小。

如苏丹上阿特巴拉电站，厂房设计要求水轮机蜗壳排水管直接引至尾水管层渗漏排水廊道，该段排水管路的高程差h≈20m，若整个管路段不设节流装置，该管路的出流速度将达到17m/s，管路将产生强烈震动和噪音。

水轮机设计中，绝大多数机组中蜗壳排水管引至尾水肘管入口附近，如图2所示。该方案排水管路高程差比较小，管路出流速度也比较小，因此我们通常不必考虑管路振动和噪音问题。

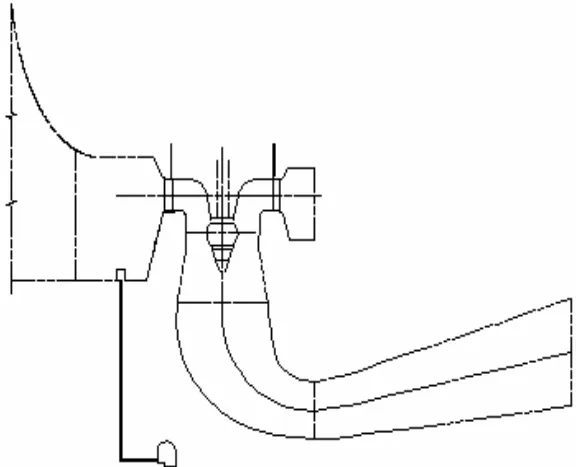
图1

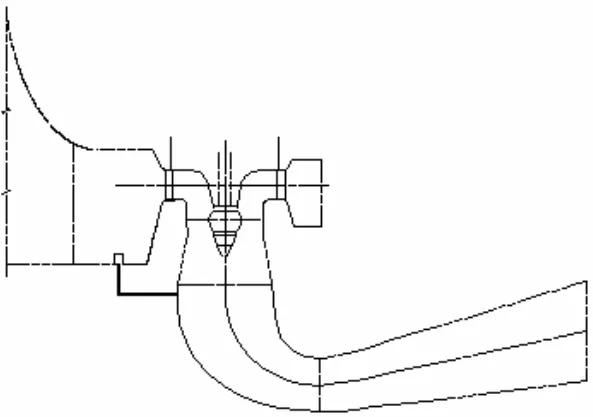
图2

3 流体力学在测量管路中的应用

3.1 管路高程差引起的测量误差及校正方法

水轮机流道压力测量中，蜗壳、尾水管等位置的测点通常通过测量管路统一引至蜗壳层或尾水锥管廊道层接压力表，这样在测点和压力表安装位置就形成高程差。当机组不同或测量位置不同，该高程差也会有差异，但通常该高程差范围在几米至十几米不等。

上述提到的测点与压力表之间的管路高程差内充满静态水，因此高程差引起的压强差为P=ρgh。若测点实际压强P1，压力表显示压强为P2，当压力表安装位置高于测点位置，则P2=P1－ρgh；当压力表安装位置低于测点位置，则P2=P1+ρgh；

其中ρ为水的密度1000kg/m3，g为当地重力加速度，h为压力表安装位置与测点位置的高程差。

对于三峡、溪洛渡、向家坝等大型机组从尾水肘管出口测点引至尾水管进人廊道处接压力表，通常高程差会有十米以上，那么该压力表的读数则小于测点真实压强至少0.1MPa，而水轮机尾水位压强一般为0.1～0.2MPa，因此由高程差引起的测压值偏差非常大，对正确评估水轮机的运行情况非常不利。比较典型、极端的情况是，当尾水管引出测量管路的压力表安装位置高于水轮机尾水位时，压力表将无读数。

水轮机中通常也用测量管路分别引蜗壳进口和尾水肘管出口处两测点的压强差作为水轮机净水头，该净水头的测量误差也在几米至十几米水头。

因此该误差影响甚大，值得我们重视并修正。

通过计算压强偏差值P=ρgh，我们建议以下几种修正方法：

（1）在压力表读数的基础上，二次校正、增加或减少压强值P=ρgh。

（2）在电站设计初期，计算压力表安装位置及测点位置的高程差。通过预定压力表的方式，将压强偏差值P=ρgh在压力表出厂前的调零阶段找正。

如压力表安装位置高于流道测点10m，那么我们预定的压力表无压力的归零点为0.1MPa。值得注意的是，此方法压力表编号需一一对应。

（3）由压力表生产商提供归零可调试压力表，压力表安装时由电站人员根据计算的压强偏差值P=ρgh对压力表进行读数校正。

3.2 全压测头介绍

圆柱绕流[2]和能量守恒[3]在水轮机测压管路中的应用。

图3为全压测头，主要用于测量蜗壳进口和肘管扩散段出口的全压值，全压测头测量的上述两位置的压差值就是水轮机净水头或水泵水轮机的净扬程。目前该全压测头在公伯峡、长河坝、观音岩等多个电站的设计中广泛应用。

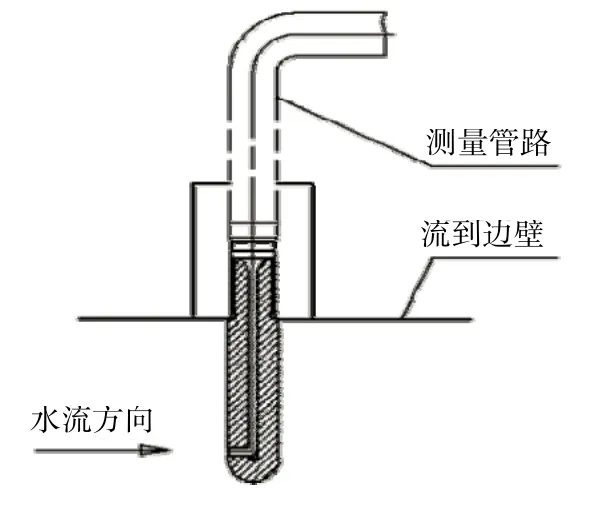
图3

下面我们用流体力学的一些原理，验证其应用的合理性。

在机组正常运行,流道比较稳定的情况下，测压头及测压管路中的水可以看作是静止不动的，因此全压测头可看成是一个圆柱，此问题为圆柱绕流问题，按流体力学中圆柱绕流进行计算。

图4中，圆柱面上任一点的压强，由伯努利方程[1]得：

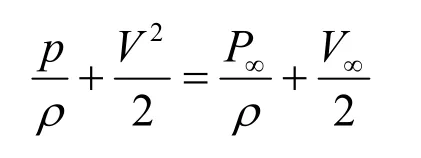
图4

同时，我们通过能量守恒来验证全压测头测量的压力为“水头”值。

流体机械计算中常引用的能量守恒公式：

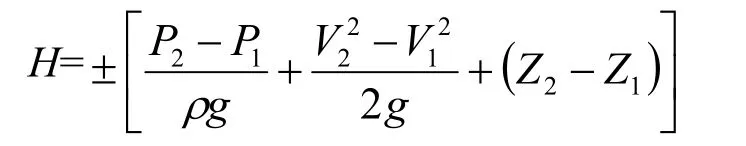
P1、V1表示无穷远处质点的压强和速度值；Z1表示无穷远处质点的高程；

P2、V2表示A点处质点的压强和速度值；Z2表示A点处质点的高程；

则流线上质点自无穷远点到A点，上式中：Z1=Z2，V2=0；

上述由能量守恒得出的结论与圆柱绕流得出的A压强值是相同的，因此我们得出结论：此全压测头测得的压力为全压水头（静压+动压=全压）。

另外，我们流体力学中的流态分析，确定全压测头深入流道的合理尺寸。

首先，我们根据水轮机流道选择模型，流体力学中管路的水力计算提供了很好的模型。一般流道计算中，我们应用雷诺数Re作为层流、湍流流态判别的依据，即Re＜2320时，管中是层流；Re＞2320时，管中是湍流；计算雷诺数时，对于非圆形断面的管道，常以当量直径de进行计算[2]。

雷诺数 Re=V×d/υ。

其中：V为流道中水流速度；d为流道的当量直径；υ为流体运动粘度系数。水轮机流道计算中：V通常为1.5～5m/s，d通常大于1m，常温下水的运动粘度系数υ=1.01× 10-6m2/s。

代入上式计算Re，则Re＞＞2320，由此得证，水轮机流道内流态为湍流。

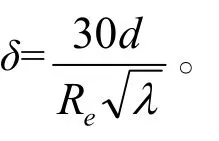
其中：λ为沿程阻力系数。

将水轮机流道参数带入上述公式中，即可得到流道内层流区的厚度δ，其厚度通常不超过几分之一毫米。因此全压测头测点处水流速度可认为是流道内的平均流速和最大流速，满足测量要求。

3.3 静压测头介绍

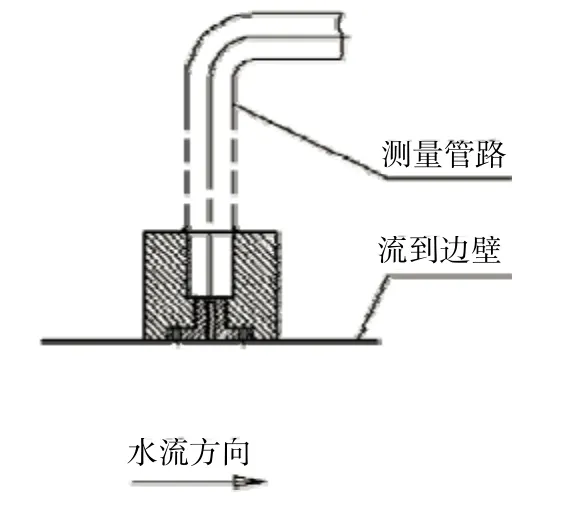
图5

静压测头测孔表面与流道表面光滑过渡，无论流道内流态为层流还是湍流其流道边壁都处在层流区，边壁处流体速度为零且测孔方向与流道内流体速度方向垂直。因此静压测头所测水压与流体速度无关，所测压力为该点流道的静压力值，满足测量要求。

同时，皮托管测流速的方法也验证了全压测头和静压测头的测量理论。

[1] 张克危,等.流体机械原理[M].北京:机械工业出版社,2000.

[2] 罗惕乾,等.流体力学[M].北京:机械工业出版社,2003.

[3] 哈尔滨大电机研究所.水轮机设计手册[M].北京:机械工业出版社,1976.