1100MW核电四极发电机并联环与主引线连接结构温度分布计算

魏燕飞，王庭山，周一工，胡建波，咸哲龙，梁旭彪

（1.上海电气电站设备有限公司发电机厂，上海 200240；2.上海电气电站设备有限公司，上海 201100）

前言

大型汽轮发电机各部件的温升对机组的运行性能有很大影响，同时也是限制发电机容量增加的一个重要原因。因此，在设计过程中对发电机各主要部件的温度分布进行计算，进而指导并调整相关设计，使运行温度能够在绝缘材料和金属材料所允许的温度限度之内，这对于保证发电机的安全可靠运行具有重要意义[1]。1100MW级核电发电机的并联环与主引线通过软连接线进行电连接，在目前设计的冷却方式和冷却参数下，连接结构的温度分布如何，将是本文计算分析的主要内容之一；另外，由于四极发电机的相带引出头较多，并联环的排布较为复杂，发电机三相6个引出线中有2个引出线采用了双倍电流环(以下简称双流环)连接结构，即并联环连接到双流环上，双流环再通过软连接线与主引线连接。双流环结构的应用使得电连接结构在电流分布上不再具有对称性，因此本文计算分析的另一重要内容是双流环与并联环之间的连接以及双流环与主引线之间的连接结构的温度分布。

对于发电机中的一些电连接部分的设计，工程设计人员通常采用估算电流密度大小的方式来确定其设计安全状况，这种方法往往根据经验给出定性的判断，但不能给出结构件中定量的温度分布情况[2]。电连接部分的温度分布与结构、冷却方式、冷却参数、连接状况等因素有很大关系，本文在充分考虑了冷却方式及参数、散热条件、连接接触的影响等因素后，应用通用有限元计算软件ANSYS作为分析计算工具，采用顺序式“电—热”耦合计算方法对百万千瓦级核电发电机软连接线结构的温度分布进行了计算，计算结果可为百万千瓦级核电发电机软连接线的具体方案设计以及双流环连接结构的设计提供一定的计算参考。

1 模型分析

1.1 物理模型的建立

在三相绕组的6个主引线电连接结构中，有4个是通过软连接结构将并联环与主引线连接起来的，图1为这种连接结构的物理模型。图1（a）所示，并联环接头两端分别与一相中的两个并联支路相连接，通过8片软连接线将并联环接头与主引线接头连接起来，主引线接头再与主引线通过焊接的方式进行连接；对应地，电流从并联环接头两端分别流入，每端的大小为I/2，通过软连接线从主引线流出，从电连接的角度来说电流分布具有对称性。连接结构通过冷却水进行冷却，如图1（b）所示，箭头线表示冷却水流的方向，并联环侧的水支路1通过一端的并联环流入到并联环接头，再流出到另一端的并联环中，主引线侧的水支路2从主引线接头的两端分别流入，最后汇流到主引线中对主引线进行冷却。

图1 并联环与主引线连接结构模型

另外2个主引线电连接结构中采用了双流环设计，并联环通过连接铜板与双流环连接，双流环再通过软连接线结构连接到主引线上，连接结构分别如图2、图3所示。电流从并联环接头两端分别流入，每端的大小同样为I/2，通过连接铜板引入到双流环中，双流环中的电流为I；再通过8片软连接线结构的连接，最后从主引线流出。此时由于双流环结构的应用，图2和图3所示连接结构中的电流分布不再具有对称性。连接结构也分别通水进行冷却，如图2（b）、图3（b）所示，箭头线表示冷却水流的方向，并联环侧的水支路通过一端的并联环流入到并联环接头，再流出到另一端的并联环中；双流环侧的水路由靠近主引线的一端注入，最后从靠近并联环接头的另一端流出；主引线侧的水支路从主引线接头的两端分别流入，最后汇流到主引线中对主引线进行冷却。

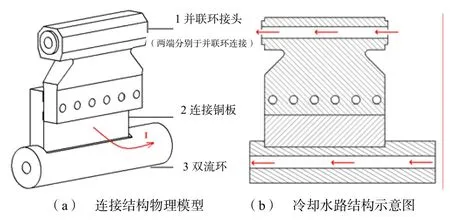
图2 并联环与双流环连接结构模型

图3 双流环与主引线连接结构模型

1.2 模型建立中的等效假定

3种模型分别如图1～3所示，计算中，软连接线和连接铜板的模型和参数在以下几个方面进行了简化和等效处理：（1）在有限元软件ANSYS中，多股铜绞线绕制的软连接线是很难建立精确模型的，因此图1以及图3中的软连接线是根据软连接线的有效导电截面积建立的等效铜排，导电截面积为480mm2，铜排的宽度保持为52mm，模型厚度约为9.2mm；（2）考虑到软连接线绞绕的影响，计算模型中铜排的长度加长了10%，即总长度为220mm；（3）软连接线中，为了减少运行过程中铜绞线间的摩擦和振动影响，要在铜绞线间填涂一定量的氟脂，这将会影响铜股线间的热量传递，使其导热性能下降。因此，在计算模型中将铜排的导热系数设定为各向异性，其中沿软连接线的连接方向设定为λy=380，其他两个方向的导热系数设定为λx=λz=200；（4）图1和图3所示软连接线与接头之间、图2并联环接头与双流环连接铜板之间均采用螺栓紧固的固定方式，接触面不是完全理想的面接触，而是若干部位的局部接触，使得总的接触面积减少了，导致局部电流密度增大（也即产生了接触电阻），损耗增加；同时，由于接触面积的减少也使得软连接线与接头之间的热传导性能变差。因此，在计算模型中，假定所有螺栓紧固的结构之间接触面积减小到整个接触面积的30%，如图4所示，在螺栓锁紧部位由于压力较大，假定接触面积主要集中在其附近。

1.3 有限元分析中的载荷参数和边界条件

根据上述物理等效模型，首先计算出50Hz稳态运行情况下连接结构的电流分布情况，进一步计算出各点的时间平均焦耳热(W)；在此基础上将电磁有限元模型转化为热分析模型，并将已计算出的焦耳热结果作为热载荷导入热分析模型中，结合冷却水的散热参数最终计算出各连接结构中的温度场分布情况。

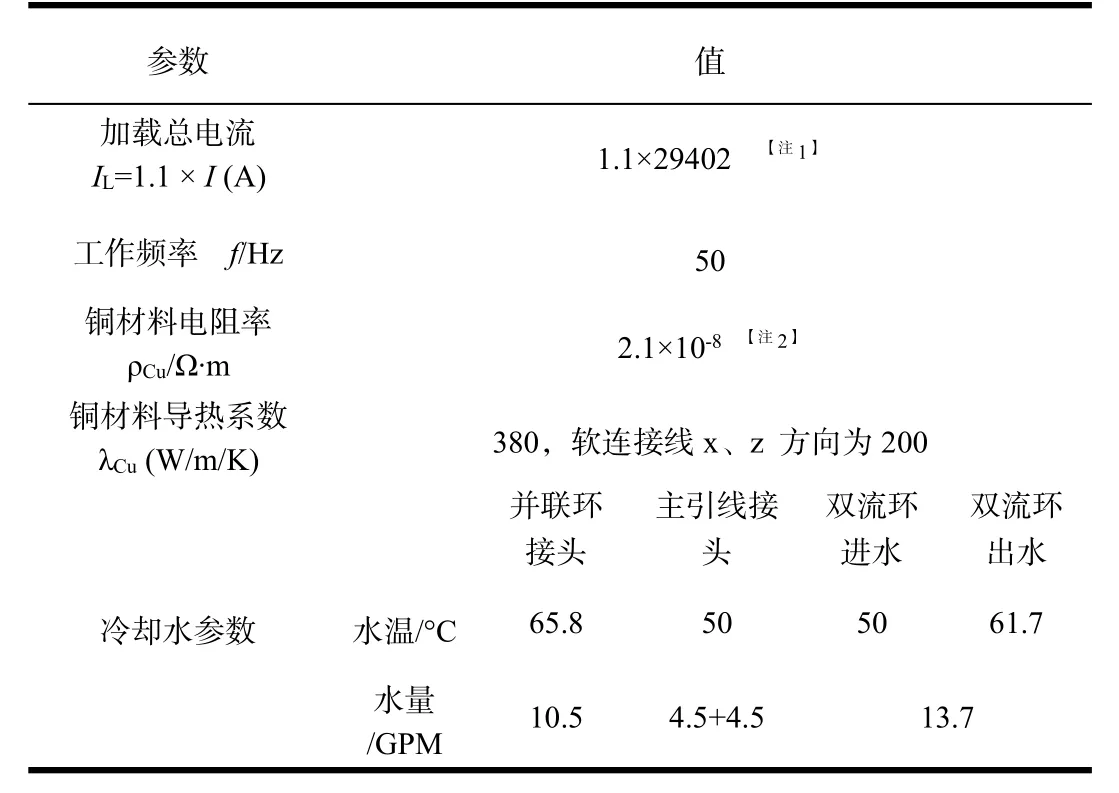
表1 电磁及温度计算参数

表1给出了计算过程中部件上承载的电载荷以及各材料参数，电磁计算中的电流载荷IL为额定电流的1.1倍，考虑了均流系数及电压波动的影响，对于有双流环的连接结构由于电流分布已经不再对称均匀，此处系数改为1.05，仅考虑电压波动的影响。冷却水的参数根据计算水温查询相关手册得到，主引线接头进水温度50°C，水流量每端为4.5GPM，汇流到主引线中的总水流量为9GPM，并联环接头水温取并联环水路中出水水温65.8°C，水流量10.5GPM，双流环中的进水水温为50°C，出水水温为61.7°C，水流量为13.7GPM。

图4 软连接铜排的端部及连接铜板接触模型

电磁计算模型要在图1～3的物理模型基础上外加自由空间模型，并在整个自由空间的外表面施加磁力线平行边界，在主引线截面上施加集中电流载荷IL，并耦合此截面上所有节点的电压自由度(认为是等位面)，指定并联环接头两端连接面上的节点电压为0，进行频率为50Hz的谐波场分析；对于温度场的ANSYS计算模型，在电磁计算ANSYS模型的基础上，删除所有气体单元，删除模型中所有节点上的自由度和载荷，并将电磁分析单元SOLID97更改为温度场分析单元SOLID70（两种单元结构相同，对实体模型不需要重新划分单元），再将电磁计算中得到的热载荷结果加载到温度场分析模型中，按照冷却水条件在通水部位设定边界条件，最后设定稳态分析进行求解即可。

2 计算结果

2.1 并联环与主引线连接结构计算结果

图5给出了连接结构的电流密度分布结果，其中图5（a）为结构的电流密度实部解，图5（b）为结构的电流密度虚部解。可以看出，由于涡流效应，结构中的电流密度分布不均匀，8片软连接线上的电流密度分布也存在差异。

连接结构的电流密度分布求解完成后，ANSYS将自动根据电流密度分布结果求解导电部件中的焦耳热密度分布，再结合水冷却参数即可计算得到连接结构的温度分布情况，结果如图6所示。可以看出，在当前设计的结构和冷却条件下，软连接线上的最高温度约为 95.5°C。

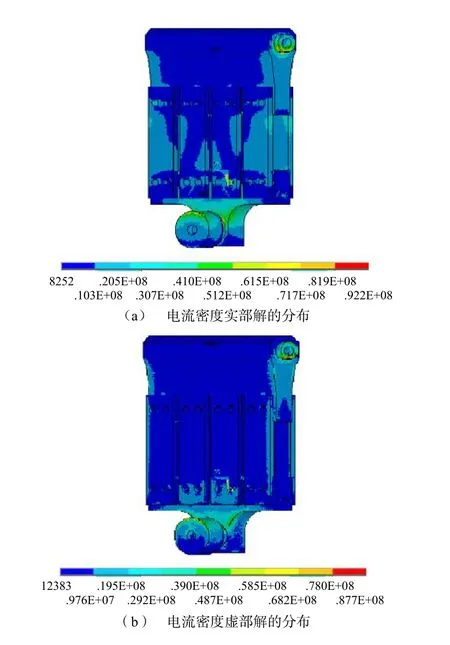
图5 并联环与主引线连接结构电流密度分布结果

图6 并联环与主引线连接结构温度分布结果

计算结果显示，当前设计结构软连接线上的最高温度达95.5°C。若能将软连接线的有效导电面积加大，可适当降低其中的电流密度，软连接线上的温度状况也会有所改善。因此，在结构允许的条件下，将软连接线的横截面有效导电面积提高到570mm2，计算模型中软连接铜排的厚度从9.2mm改为10.9mm，其他条件不变。计算结果如图7所示，可以看出，适当加大软连接线的横截面导电面积后，软连接上的最高温度约为91°C，有所改善。

图7 软连接线调整后连接结构温度分布结果

2.2 并联环与双流环连接结构计算结果

图8（a）为并联环与双流环连接结构的温度分布结果。可以看出，由于双流环结构的不对称性，电流流向遵循“最短路径”原则，电流密度分布以及温度分布很不均匀，靠近内侧的温度高，最高温度约达124°C。

为了适当降低连接结构上的热点温度，将并联环接头以及连接铜板沿双流环方向加宽50mm，从而加大电流流向的“路径”距离。图8（b）为调整后连接结构的温度分布结果，可以看出，最高温度降低到约115°C，结构的适当调整可有效改善结构上的热点温度。

2.3 双流环与主引线连接结构计算结果

图9（a）为双流环与主引线连接结构的温度分布结果，软连接线的有效截面面积为480mm2。同样，由于双流环结构的不对称性，电流密度分布以及温度分布很不均匀，靠近内侧的软连接线上的电流密度大，温度最高，最高温度约达125°C。

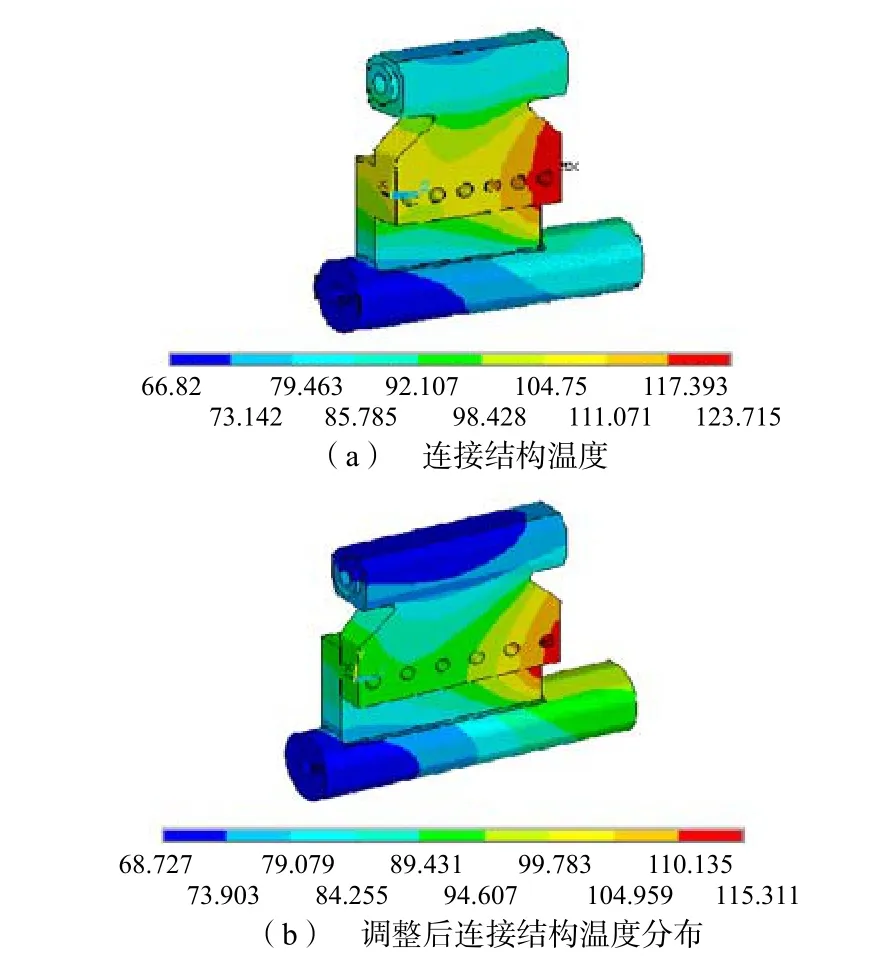
图8 并联环与双流环连接结构温度分布结果

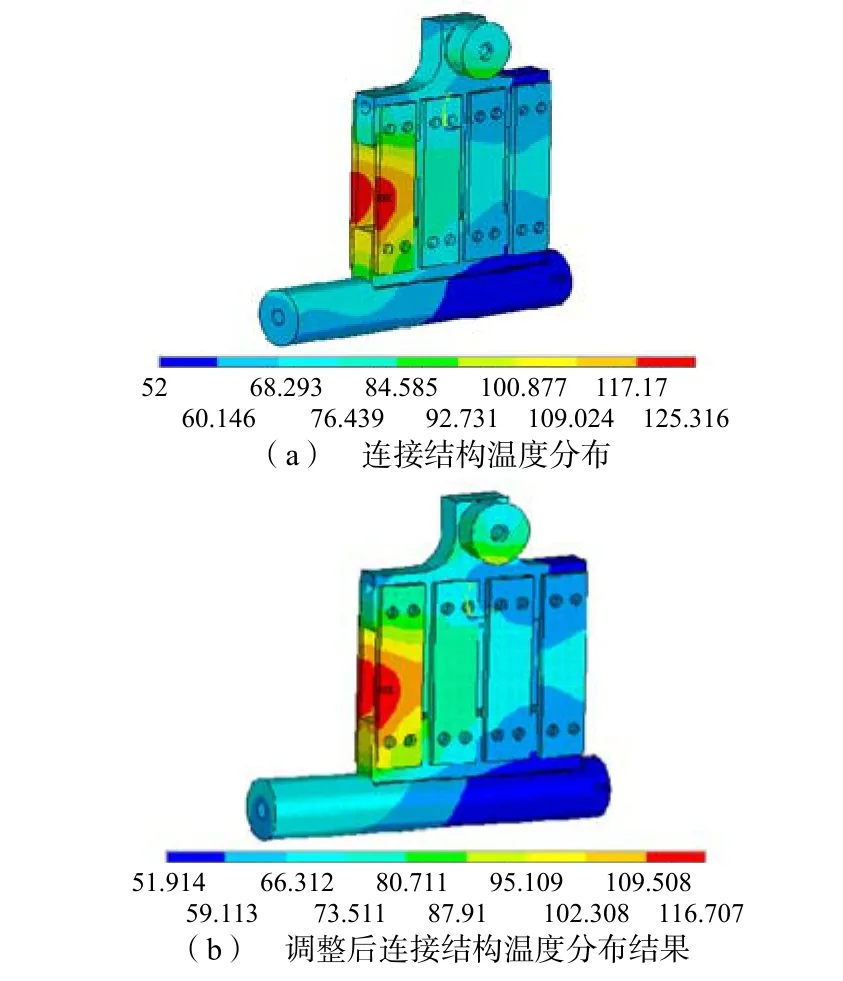
图9 双流环与主引线连接结构温度分布结果

与模型1计算相同，将软连接线的横截面有效导电面积提高到570mm2，即软连接铜排的厚度从9.2mm改为10.9mm，计算结果如图9（b）所示，可以看出，加大软连接线的横截面导电面积后，软连接上的最高温度约为116.7°C，有效改善了软连接线上的热点温度。

3 分析与结论

本文基于有限元软件ANSYS，对百万千瓦级核电发电机并联环与主引线间的连接结构上的温度分布进行了计算分析，计算模型充分考虑了实际运行中影响连接结构温度分布的各种因素（如填充氟脂的影响、接触部位的影响、电流波动的影响等），计算结果表明，双流环与主引线间的连接结构中最高温度约为125°C，适当加大软连接线的导电截面积为570mm2后(即软连接线加厚)，可有效改善其温度分布状况，最高温度约为116.7°C。对于并联环与双流环的连接结构中，在设计允许的条件下，沿双流环方向适当加宽并联环接头以及连接铜板，也可有效改善连接结构上的热点温度，在本文中，加宽50mm后最高温度从124°C降到115°C。

另外，对计算模型的合理性和计算结果的有效性还需作如下几点说明：

（1）实际使用中的软连接线是多股铜线绞绕而成的，受涡流效应的影响较小，其中的电流密度是比较均匀的；计算模型中将其等效为铜排，涡流效应使铜排中的电流密度不均匀(图5所示)，损耗较实际情况有所增加。

（2）实际运行中软连接线与接头之间虽然不是完全理想的面接触，但贴合还是比较紧密的，之间的空气隙非常小；计算模型中为了能够有效剖分并适当减少计算单元，此处的空气隙很大(1.5mm)，如图4所示。因此，计算模型中此处的导热效果要比实际情况差一些。

（3）实际运行中虽然软连接线部位包有绝缘，导热性能较差，但外面的冷氢还是能够带走部分热量；而计算模型中假定此处是绝热的。

因此，发电机在实际运行中其连接结构上的热点温度比计算温度还要低一些。综合以上的分析，本文所给出的计算结果是合理有效的，能够满足并指导实际工程设计。

[1] Wei Yanfei,Qi Le,Wang Tingshan.Temperature Calculation on Phase Lead Connecting Structures of 1100MW Generator Stator Parallel Rings[J].Advanced Materials Research,2012,(433-440),7131-7137.

[2] 汪耕,李希明.大型汽轮发电机设计、制造与运行[M].上海:上海科学技术出版社,2000.