掌子面推进过程围岩应力及裂隙发育规律

刘立鹏，汪小刚，贾志欣，段庆伟，贾龙

(1.中国水利水电科学研究院 岩土工程研究所，北京，100048；2.中国地质科学研究院 岩溶地质研究所，广西 桂林，541004)

岩体不仅是一种单纯的地质材料，同时亦处于复杂的应力环境中。地下巷道工程开挖，掌子面逐渐推进，初始平衡地应力场遭到人为扰动，产生应力重分布，而这一过程包含应力大小及方向的同时变化过程。传统岩石(体)力学理论中，将无较大结构面岩体视为均质、各向同性体，并基于平面应变假设，利用弹塑性力学计算得到洞室开挖后洞壁围岩应力分布特征，进而在这一基础上提出支护等方案[1−3]。然而实际工程中，无论采用钻爆法抑或 TBM 技术施工，距掌子面一定范围内围岩应力量值及方向皆随掌子面推进而逐步动态变化。此外，围岩裂隙发育不仅与应力大小有关，同时生成方向亦随着主应力方向变化而变化[4−6]。国内外学者认识到应力变化对围岩稳定的影响，并对其进行了研究分析[7−9]，但一般未考虑掌子面推进这一工程实际情况[10−12]，且已有研究中未充分考虑主应力方向变化对裂隙发育的影响。锦屏二级水电站施工排水洞开挖建设中，围岩由于开挖诱生较多平行洞壁次生裂隙，同时伴随有围岩片帮等等级较高岩爆灾害现象，威胁施工人员人身安全的同时，对工程建设进度造成了极大的影响。本文作者利用数值模拟软件，结合室内岩石试验，对其一典型洞段(SK11+000)掌子面推进过程中围岩应力大小、方向及裂隙发育角度变化等情况进行详尽研究分析，以加深对洞壁围岩应力动态变化特征及围岩裂隙化认知，可对地下洞室工程围岩支护措施及支护时机的选择提供借鉴。

1 围岩应力解析解及裂隙优势发育方位角

1.1 围岩应力解析解

假设地下一定埋深岩体垂直应力为PV，水平应力为PH且均匀分布，侧压系数K=PH/PV(如图1所示)。圆形洞室开挖后洞壁围岩径向应力σr、切向应力σθ及剪应力τrθ分别为[1]

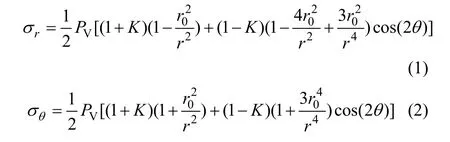
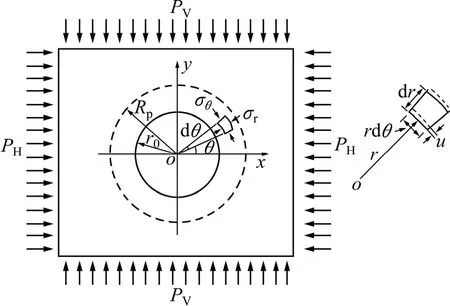
图1 围岩应力计算简图[1]Fig.1 Relationship between σ1 and σ3[1]

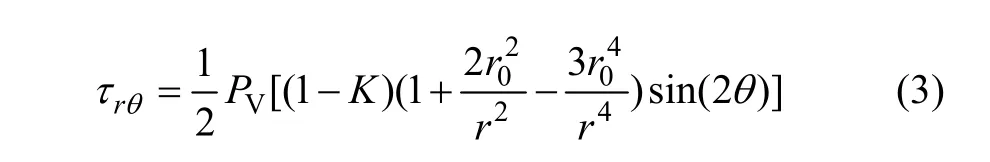
式中：r0为洞室半径；r为径向距离；θ为水平轴夹角。

则围岩中任意一点(r，θ)处的最大主应力σ1和最小主应力σ3分别为：

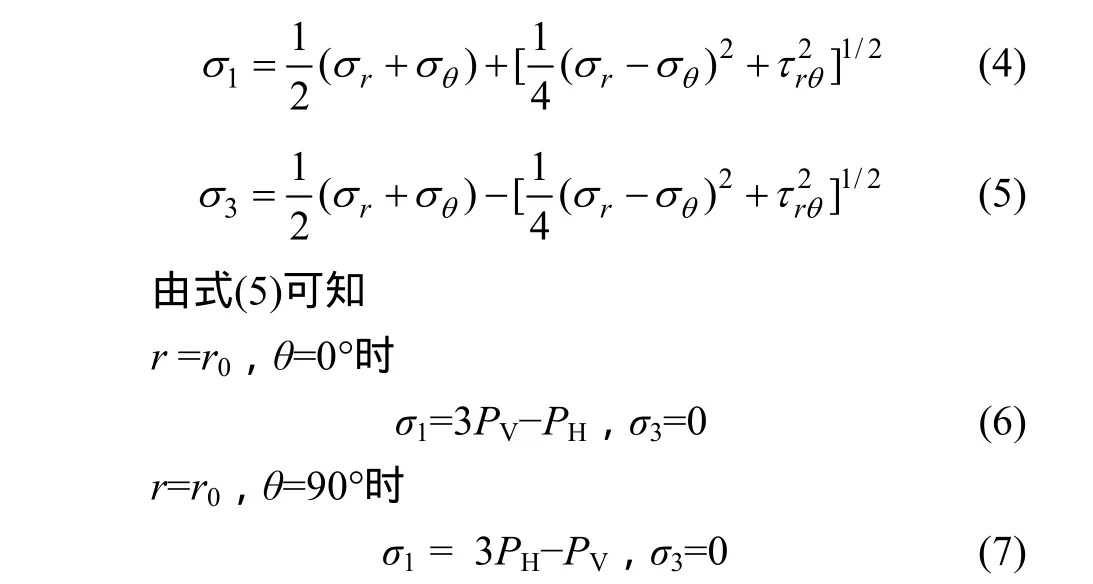
上述洞壁围岩应力重分布结果以平面应变为前提假设，利用弹性力学所得解析解，其中未考虑施工动态过程对围岩应力重分布的影响(量值及方向)，无法定量分析施工掌子面推进过程对围岩应力变化的影响，具有一定局限性，但由于简单适用性，在工程设计及稳定性计算中一直被采用[1]。

1.2 裂隙优势发育方位角

由于成岩、构造运动及其他外部营力的作用，岩体中一般具有一定的宏观和微观裂隙。外部营力改变，裂隙周边特别是端部，产生应力集中现象，进而在缝端开始破坏。从应力作用角度考虑，影响裂隙生成、扩展及融合的主要因素有以下 2点：(1) 主应力差量值(如图2所示)；(2) 主应力作用方向(如图3所示)。裂纹生成、扩展及贯通并最终导致整个岩体单元破坏。

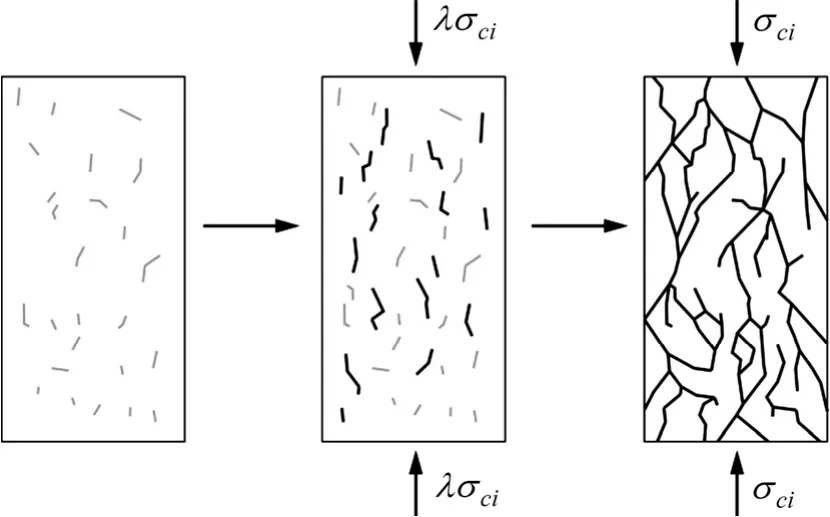
图2 主应力对裂隙发育的影响Fig.2 Influence of principal stress on development of crack

图3 主应力作用方向对裂隙发育的影响[8]Fig.3 Influence of principal stress orientation on development of crack[8]

假设岩石中含有大量的方向杂乱的细微裂隙，其中有一系列如图4所示，它们的长轴方向与最大主应力σ1夹角为β。由Griffith强度理论可知：岩石内部已有裂隙中最优发育方向随所处应力状态不同而不同[13]：

当σ1+3σ3＞0时，优势裂隙方位角

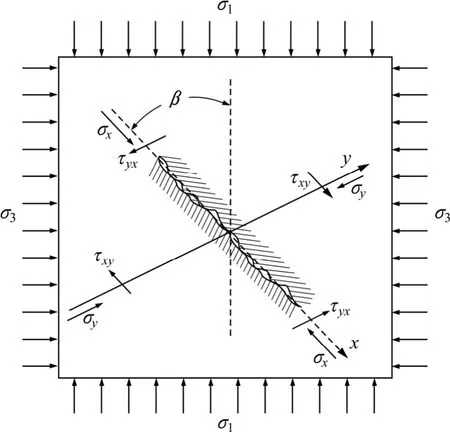
图4 细微裂隙受力示意图Fig.4 Diagram of stress on fracture

当σ1+3σ3＜0时，优势裂隙方位角

由式(8)和(9)可知不同应力情况优先破裂裂隙方位不同：

(1) 一般受力状态下，岩石中的细微裂隙优势发育方位角为 0°～45°；

(2) 单轴压缩状态，岩石中的细微裂隙优势发育方位角为30°；

(3) 单轴受拉状态，岩石中的细微裂隙优势发育方位角为0°；

(4) 静水压力状态，岩石中的细微裂隙优势发育方位角为45°。

即无论所处何种应力状态下，岩体次生裂隙的产生、扩展和贯通基本沿最大主应力方向发生，或与最大主应力方向成一较小夹角[14−16]。同时岩体破坏时，主裂纹的扩展方向除与裂纹的力学性质有关外，还受已有微裂隙分布、空隙等的影响[15]，而对地下洞室开挖主应力量值及方向变化特征的详尽研究将进步深化对裂隙产生、扩展及贯通的认知。

2 围岩应力及裂隙发育变化特征

锦屏二级水电站位于四川省凉山州境内的雅砻江锦屏大河弯处雅砻江干流上，地处青藏高原向四川盆地过渡的地貌斜坡地带。锦屏二级水电站为一低闸、长隧洞、高水头、大流量的引水式电站。电站建成后，将供电川渝并参与西电东送，是雅砻江上水头最高，装机规模最大的一座水电站。电站主要有4条引水隧洞、2条辅助洞、1条施工排水洞及地下主厂房组成，施工排水洞长16.7 km，圆形，洞径7.2 m[17]。施工排水洞开挖过程中，由于开挖卸荷及围岩应力重调整作用，在侧壁浅部位围岩中生成小角度进平行洞壁张拉裂隙(见图5)，较深部位生成具有一定弧度的剪切裂隙(见图6)，同时发生等级不一的应变型岩爆灾害[17]。

以锦屏二级水电站施工排水洞SK11+000桩号段信息为基础建立三维数值分析计算模型，利用FLAC3D研究掌子面推进过程中洞壁围岩应力变化特征，并自应力角度解释围岩裂隙化原因。洞室三维模型如图7所示。图7中：洞轴方向为z轴，竖直方向为y轴，水平垂直洞轴方向为x轴。围岩力学参数及初始地应力如表1所示，初始应力场以自重应力作用为主[18−19]。为监测围岩应力变化特征，垂直洞轴设置一监测平面，侧壁及洞顶方向各设置8个监测点，监测点布置如图8所示。

图5 侧壁浅部小角度张拉裂隙Fig.5 Tension fractures with small angle in sidewall rockmass

图6 具有一定弧度的破坏面Fig.6 Failure surface with definite angle

图7 数值分析模型Fig.7 Model of numerical simulation

表1 围岩力学参数及初始地应力Table 1 Parameters of rock mass and in-situ stress

图8 监测点布置示意图Fig.8 Position of monitor points

监测点与洞壁间的距离如表2所示。

表2 监测点与洞壁距离Table 2 Distance form monitor points to rock wall

对施工排水洞进行全断面一次性开挖，而随掌子面与监测面距离不同，开挖进尺略有变化。

2.1 应力变化规律

掌子面推进过程侧壁及洞顶主应力变化及最大主应力方向如图9和10所示，其中侧壁最大主应力方向为y−z面投影相对y轴的位置，而洞顶则为x−y面相对x轴位置，掌子面穿过监测面后L标识为负。

由图9和10可知：掌子面开挖接近至距离监测面约1倍洞径(D，其中D=7.2 m)时，洞顶及侧壁最大主应力、中主应力及最小主应力皆开始出现增大趋势，并一直保持至掌子面与监测面重合时，但洞壁不同部位，应力增加值不同。掌子面开挖穿过监测面后，洞顶及侧壁中主应力σ2及最小主应力σ3则发生猛烈降低，表现出明显卸荷特征。而洞壁不同部位最大主应力表现不同变化特征，如侧壁最大主应力σ1继续增高(垂直初始应力场最大主应力方向)，围岩应力逐步变大，最终趋于与弹性解析解相等(约2D处)，而洞顶则急剧降低，并最终保持为平面应变解析解附近变化(32 MPa)，即施工排水洞开挖，应力重分布具有一定的影响范围。

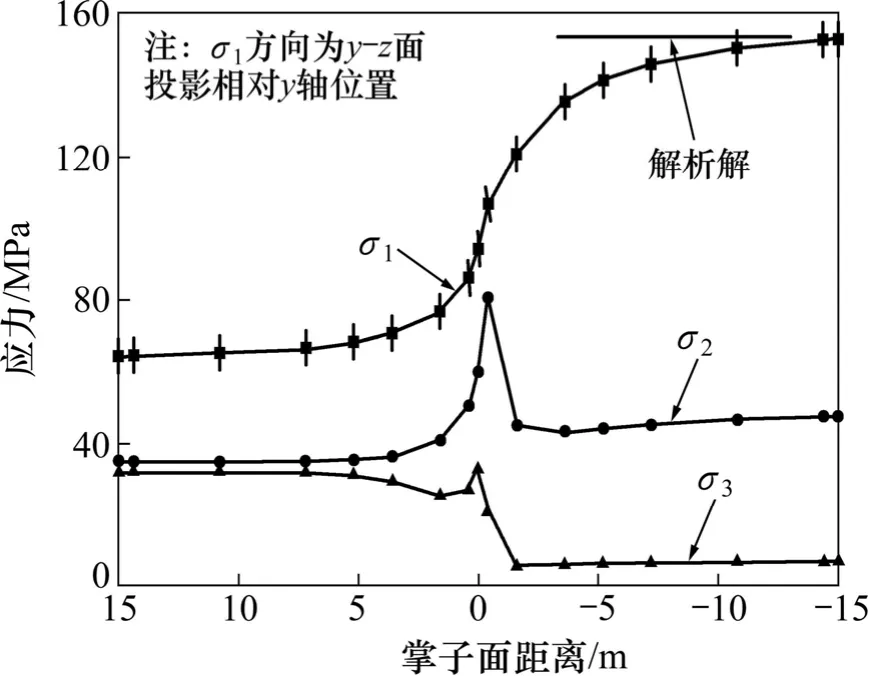
图9 侧壁围岩主应力变化(H1监测点)Fig.9 Principal stress in tunnel sidewall rock mass while tunnel face advancing(H1 point)

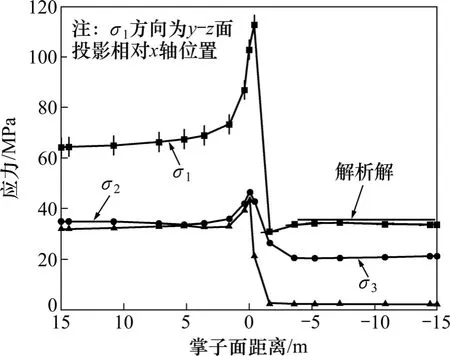
图10 洞顶围岩主应力变化(V1监测点)Fig.10 Principal stress in tunnel roof rock mass while tunnel face advancing(V1 point)

侧壁围岩及洞顶围岩最大主应力方向变化趋势不同，侧壁在掌子面接近及穿过监测面较小范围内最大主应力相对y轴仅发生较小偏转，而洞顶最大主应力σ1方向在掌子面未穿过监测面时基本保持初始应力状态方向，变化较为平稳，穿越监测面后则立即发展至与x轴平行状态，洞顶围岩中主应力方向发生较大变化。

2.2 应力差变化规律

洞壁围岩裂隙生成及屈服同时与围岩主应力差相关[20−22]，Mohr理论、Mohr-Coulomb准则、最大剪应力准则、Lundborg理论等及室内外试验皆表明：剪应力对岩体破坏具有控制作用，而这一量值变化可用主应力差值进行反映。掌子面推进过程中洞顶及洞壁主应力差变化如图11所示。

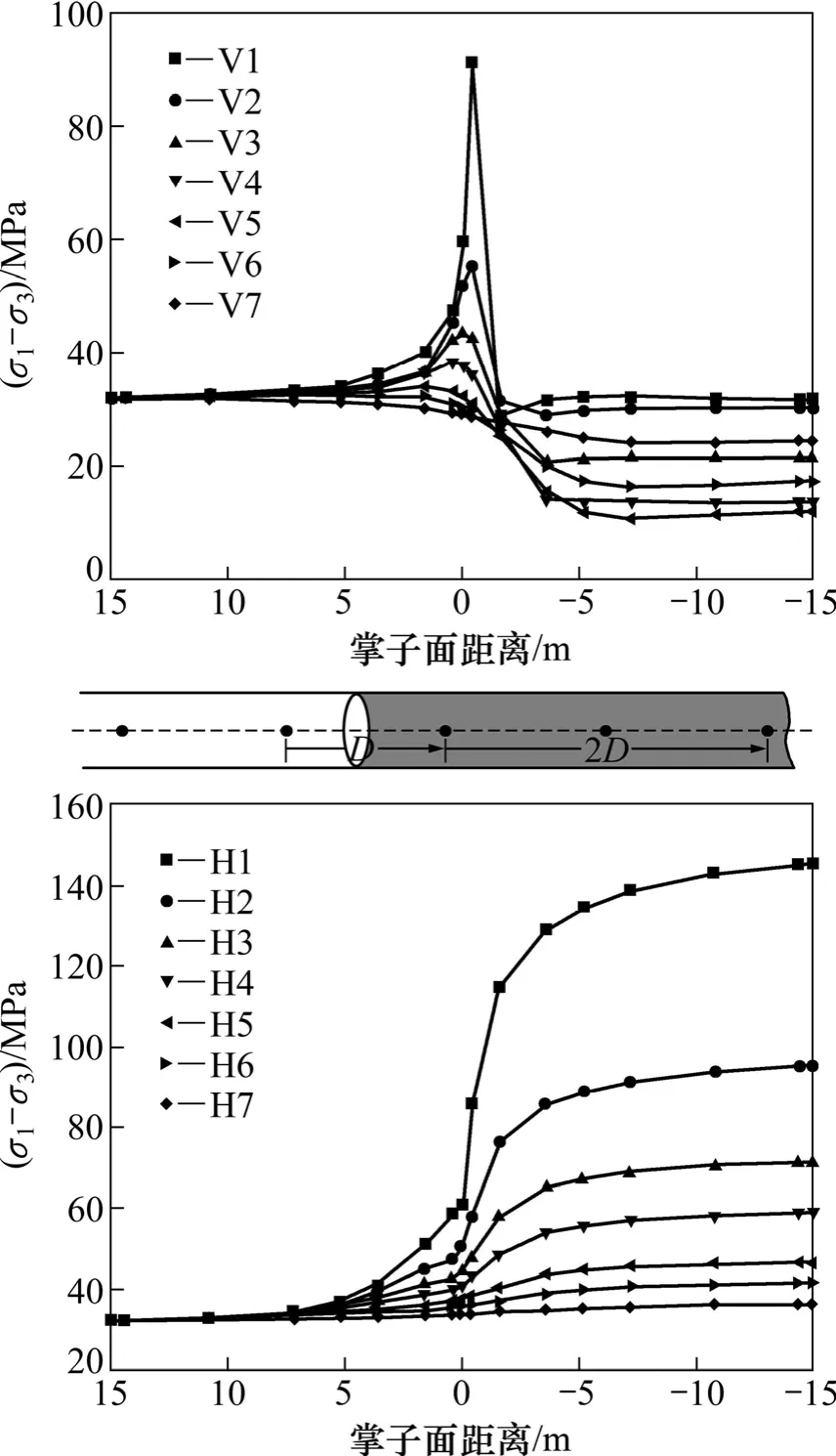
图11 洞壁围岩主应力差变化Fig.11 Differential stress in wall rock while tunnel face advancing

由图11可知：掌子面推进动态过程中，侧壁及洞顶主应力差发生不同变化。掌子面开挖至监测面时，侧壁及洞顶主应力差皆为增加过程，即剪应力增加。穿过监测面后，侧壁量值表现为继续增加。洞顶部位，开挖掌子面穿过监测面后，主应力差则为急剧降低过程。监测点与洞壁之间距离增加，应力差逐渐减小，并最终趋于初始应力场主应力差。掌子面推进过程中洞顶及侧壁浅表部围岩主应力差对比如图12所示。

由图12可知：在掌子面达到监测面时，主应力差皆保持90 MPa附近，而穿过监测面后洞顶与侧壁的主应力差相差较大，对应相同围岩强度(启裂强度)，则在掌子面穿过监测面后续过程中，洞顶及侧壁表现出不同的裂隙发育及屈服破坏特征，洞壁不同部位岩体分别对应不同的稳定状态。

图12 侧壁及洞顶主应力差变化Fig.12 Deviatoric stress in wall rock while tunnel face advancing

2.3 主应力方位变化规律

对H1和V1监测点掌子面推进过程中主应力方位变化进行监测，具体特征如图13和14所示，其中：

(1) 水平面为x−z面，倾向为与x轴正方向夹角，其中x正方向为0°方向，顺时针旋转为正；

(2) 主应力倾角为主应力与投影面x−z面之间的夹角。

图13 掌子面推进侧壁最大主应力方向变化(H1)Fig.13 Maximum principal stress dip and trend in tunnel sidewall rockmass while tunnel face advancing(H1 point)

由图13可知：掌子面推进过程中，侧壁最大主应力倾角变化不大，基本保持 85°～90°，仅在掌子面与监测面之间距离为−0.25D～0.25D内发生较小变化，并最终趋于竖直状态。掌子面开挖至监测面0.25D范围时，侧壁最大主应力倾向发生变化，经历距监测面−0.25D～0.25D范围内的不稳定变化后，逐渐向x轴方向靠拢，最终与x轴保持平行(水平垂直洞轴方向)。

图 14所示为掌子面推进洞顶最大主应力方向变化特征(V1)。由图14可知：随着掌子面逐渐推进，监测面处洞顶围岩最大主应力倾角逐渐减小，并在穿过监测面约0.25D距离后，倾角变化至0°，即与水平面保持平行。掌子面未穿过监测面时，倾向基本保持不变，而在穿过0.25D距离后突降至0°，即与x轴保持平行，进而洞顶围岩最大主应力平行水平面同时垂直洞室轴线。

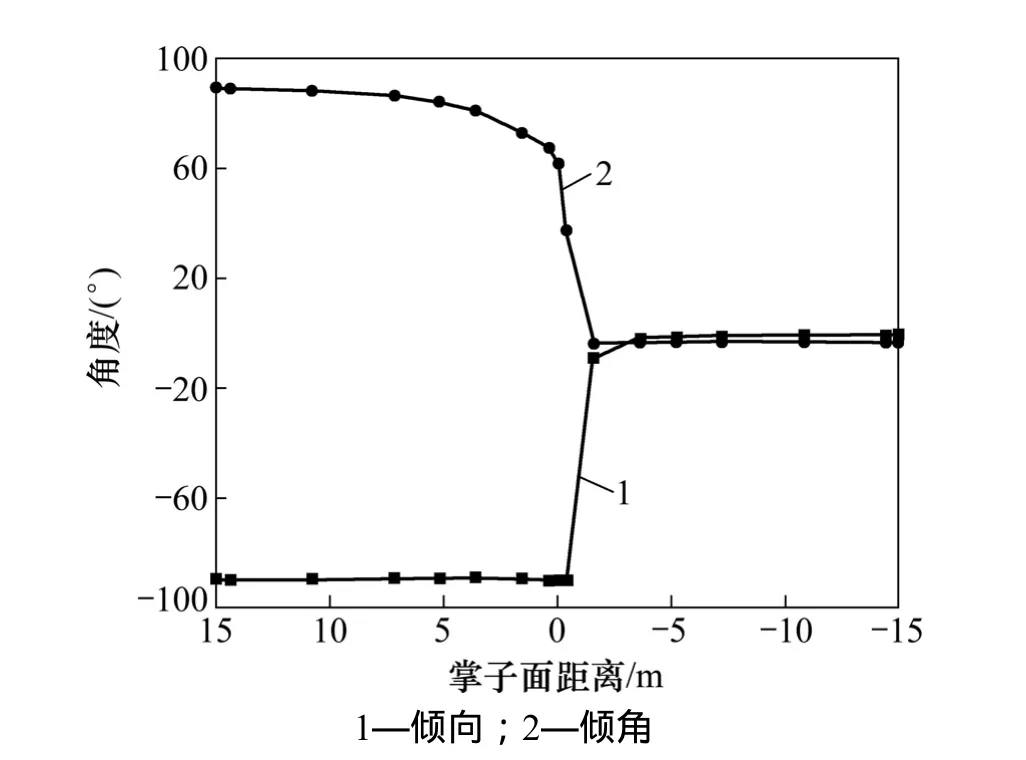
图14 掌子面推进洞顶最大主应力方向变化(V1)Fig.14 Maximum principal stress dip and trend angles in tunnel roof rockmass while tunnel face advancing(V1 point)

2.4 裂隙优势发育角度规律

由式(8)和(9)可知：不同应力组合下，裂隙优势发育角度不同，此处，不考虑最大主应力方向的变化，掌子面推进过程中，洞壁侧壁、洞顶围岩裂隙优势发育角度如图15和16所示。

由图15可知：裂隙优势发育角β随掌子面与监测面距离的减小而逐渐减小。岩体单元与洞壁距离不同，β变化幅度不同，一般随着岩体单元与开挖洞壁间距离的增大而逐渐增大，及接近水平洞壁范围，生成小角度与洞壁近平行裂隙(图5)，而随着深度的增加，则逐渐变为具有一定弧度裂隙(图6)。同时，由图15可知：裂隙角度变化基本发生在与掌子面一倍洞径(D)范围内，并在一定深度基本保持原裂隙优势方位角不变，即开挖对这一范围外岩体应力分布及裂隙扩展角度变化等基本无影响。

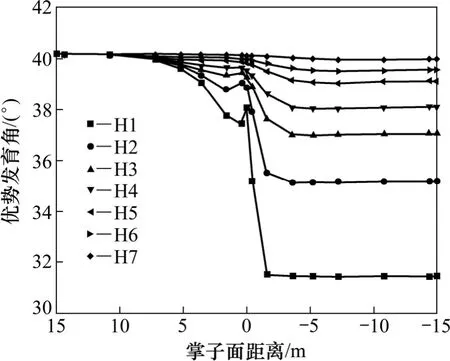
图15 掌子面推进侧壁围岩裂隙优势发育角Fig.15 Angle more favorable to break in tunnel sidewall rockmass while tunnel face advancing

图16 掌子面推进洞顶围岩裂隙优势发育角Fig.16 Angle more favorable to break in tunnel roof rockmass while tunnel face advancing

由图16可知：洞顶岩体单元与洞壁距离不同，掌子面推进过程中，岩体裂隙优势发育角β变化特征不同。掌子面接近监测面过程中，洞顶不同深度岩体中β分别表现出增加及降低特征。掌子面穿过监测面后，洞顶浅表部围岩β表现突然降低特征，而较深部位岩体中β则表现明显增加特征，这表明对于洞顶不同部位围岩，开挖应力扰动方式不同，微裂隙起始扩展位置不同，扰动范围相较侧壁不同。

当掌子面距离监测面一倍洞径(D)时，由于应力组合发生变化，侧壁岩体裂隙优势发育角度β相应发生变化。掌子面距离监测面距离不同，侧壁及洞顶岩体β不同。掌子面穿过监测点一倍洞径后，基本保持某一特定值不变，所形成裂隙一般具有相近产状。由于所表征裂隙优势发育角度为与最大主应力之间角度的角度，及裂隙优势发育角度同时随最大主应力角度变化而变化，进而侧壁围岩中生成环洞壁近平行裂隙，而随着深度的增加生成具有一定弧度裂隙。

3 结论

(1) 掌子面开挖至距离监测面约一倍洞径时，洞壁主应力及主应力差开始出现增大趋势，并一直保持至掌子面与监测面重合时，但不同部位增加幅度不同。掌子面穿过监测面后，洞顶及侧壁中主应力及最小主应力发生猛烈降低，表现出明显的卸荷特征，而洞壁不同部位围岩最大主应力表现不同变化特征，侧壁最大主应力及差应力继续增高，洞顶急剧降低，主应力最终于约两倍洞径处达到解析解。监测点与洞壁之间距离增加，应力差逐渐减小，并最终趋于初始应力场主应力差，即施工排水洞开挖，应力重分布具有一定的影响范围。

(2) 掌子面推进过程中侧壁及洞顶最大主应力方向变化特征不同。整个开挖过程中，侧壁最大主应力倾角变化不大，一般保持 90°左右，仅在 0.25D距离范围内发生较小变化，倾向则在掌子面到达监测面附近时发生较大的变化，穿过监测面后则逐渐发展至水平垂直洞轴方向。洞顶最大主应力倾向与倾角主要在掌子面接近监测面0.25D距离时开始变化，当掌子面穿过监测面0.25D距离后，最大主应力基本保持竖直垂直洞轴方向。

(3) 掌子面接近监测面一倍洞径范围内，洞壁围岩微裂隙优势发育角β开始变化，侧壁与洞顶表现不同特征。掌子面穿过监测面后，侧壁围岩β一般减小，而洞顶岩体单元β既有减小又有增大变化，洞室开挖对洞壁不同部位围岩应力具有不同的重分布作用。

(4) 初始应力场一般为自重应力与构造应力联合作用的结果，对于不同工程地质环境，分别以自重应力或构造应力作用为主，并与洞轴呈不同角度相交出现。此外，地质构造(褶皱、断层等)对局部应力场分布亦具有较明显影响。文中基于锦屏二级水电站施工排水洞 SK11+000桩号段自重应力为主的应力场环境，研究分析了掌子面推进过程中围岩应力及裂隙演化规律。由于实际工程所处地质环境及开挖洞形等基本情况不同，围岩应力动态发展及裂隙发育规律将具有一定变化。

[1] 徐志英.岩石力学[M].3版.北京: 中国水利水电科学出版社,1993: 110−112.XU Zhiyin, Rock mechanics[M].3rd ed.Beijing: China Water Power Press, 1993: 110−112.

[2] Hoek E, Brown E T.Underground excavations in rock[M].London: The Institution of Mining and Metallurgy, 1980: 76−79.

[3] Hoek, E, Kaiser P K, Bawden W F.Support of underground excavations in hard rock[M].Rotterdam: A.A.Balkema, 1995:81−87.

[4] Read R S.20 years of excavation response at AECL’s Underground Research Laboratory[J].International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1251−1275.

[5] Potyondy O D, Cundall P A.A bonded-particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences,2004, 41(8): 1329−1364.

[6] Cho N, Martin C D, Sego D C.A clumped particle model for rock[J].International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 997−1010.

[7] 刘立鹏, 姚磊华, 王成虎, 等.地应力对脆性岩体洞群稳定性的影响[J].中南大学学报: 自然科学版, 2010, 41(2): 709−714.LIU Lipeng, YAO Leihua, WANG Chenghu, et al.Influence of in-situ stress on stability of underground openings in hard rock[J].Journal of Central South University: Science and Technology, 2010, 41(2): 709−714.

[8] Eberhard T.Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face[J].International Journal of Rock Mechanics and Mining Sciences, 2001, 38(4):499−518.

[9] Moriyaa H, Fujita T, Niitsuma H, et al.Analysis of fracture propagation behavior using hydraulically induced acoustic emissions in the Bernburg salt mine, Germany[J].International Journal of Rock Mechanics and Mining Sciences, 2006, 43(1):49−57.

[10] 杨为民, 李术才, 陈卫忠, 等．琅琊山抽水蓄能电站地下厂房洞室开挖与支护数值模拟[J].岩石力学与工程学报, 2004,23(增 2): 4966−4970.YANG Weimin, LI Shucai, CHEN Weizhong, et al.Numerical simulation of excavation and support for underground power-house of Langyashan pumped-storage power station[J].Chinese Journal of Rock Mechanics and Engineering, 2004,23(Sup.2): 4966−4970.

[11] 张农, 许兴亮, 李桂臣.巷道围岩裂隙演化规律及渗流灾害控制[J].岩石力学与工程学报, 2009, 28(2): 330−335.ZHANG Nong, XU Xingliang, LI Guichen.Fissure-evolving laws of surrounding rock mass of roadwang and control of seepage disasters[J].Chinese Journal of Rock Mechanics and Engineering, 2009, 28(2): 330−335.

[12] 杨天鸿, 赵兴东, 冷雪峰, 等.地下开挖引起围岩破坏及其渗透性演化过程仿真[J].岩石力学与工程学报, 2003, 28(增刊1):2386−2389.YANG Tianhong, ZHAO Xingdong, LENG Xuefeng, et al.Numerical simulation on failure process of overburden rock strata and permeability evolution caused by mining excavation[J].Chinese Journal of Rock Mechanics and Engineering, 2003,28(Sup.1): 2386−2389.

[13] Griffith A A.Theory of rupture[C]//Proceedings of the First Congress of Applied Mechanics.Delft, 1924: 55−63.

[14] 葛修润, 任建喜, 蒲毅彬, 等.岩石细观损伤扩展规律的 CT实时试验[J].中国科学: E辑, 2000, 30(2): 104−111.GE Xiurun, REN Jianxi, PU Yibin, et al.Research on crack developing rules by using real-time scanning CT test[J].Science in China: Series E, 2000, 30(2): 104−111.

[15] 陈蕴生, 李宁, 韩信, 等.非贯通裂隙介质裂隙扩展规律的CT试验研究[J].岩石力学与工程学报, 2005, 24(15):2665−2670.CHEN Yunsheng, LI Ning, HAN Xin, et al.Research on crack developing process in non-interpenetrated crack media by using CT[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(15): 2665−2670.

[16] 刘冬梅, 蔡美峰, 周玉斌, 等.岩石裂纹扩展过程的动态监测研究[J].岩石力学与工程学报, 2006, 25(3): 467−472.LIU Dongmei, CAI Meifeng, ZHOU Yubin, et al.Dynamic monitoring on developing process of rock cracks[J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3):467−472.

[17] 刘立鹏, 汪小刚, 贾志欣, 等.锦屏二级水电站施工排水洞岩爆机理及特征分析[J].中南大学学报: 自然科学版, 2011,42(10): 3150−3156.LIU Lipeng, WANG Xiaogang, JIA Zhixin, et al.Analysis of mechanism and characteristic of rockburst in drainage-hole of Jinping II hydropower station[J].Journal of Central South University: Science and Technology, 2011, 42(10): 3150−3156.

[18] 陈秀铜, 李璐.锦屏二级水电站引水隧洞区域三维初始地应力场反演回归分析[J].水文地质工程地质, 2007(6): 55−64.CHEN Xiutong, LI Lu.Inverse analysis of initial field stress for Jinping-2 hydropower station tunnel area[J].Hydrogeology &Engineering Geology, 2007(6): 55−64.

[19] 刘立鹏.锦屏二级水电站施工排水洞岩爆问题研究[D].北京:中国地质大学(北京)工程技术学院, 2011: 41−44.LIU Lipeng.Study on rockburst of drainage tunnel in Jinping II hydropower station[D]. Beijing: China University of Geoscience(Beijing).School of Engineering and Technology,2011: 41−44.

[20] Carter B J.Size and stress gradient effect on fracture around cavities[J].Rock Mechanics and Rock Engineering, 1992, 23(3):167−186.

[21] Martin C D.Seventeenth Canadian Geotechnical Colloquium:The effect of cohesion loss and stress path on brittle rock strength[J].Canadian Geotechnical Journal, 1997, 34(5):698−725.

[22] Germanovish L N, Dyshin A V.Fracture mechanisms and instability of openings in compression[J].International Journal of Rock Mechanics and Mining Sciences, 2000, 37(1/2):263−284.