用摩擦角概念理解自锁问题

胡双根 刘 燕

(新余市第四中学 江西 新余 338031)

2012年全国理科综合能力测试卷第24题是一道与生活现象紧密结合的问题.从我省阅卷统计来看，第二问得分不足3分，得分之低，令人叹息.

【原题】拖把是由拖杆和拖把头构成的擦地工具(图1).设拖把头的质量为m，拖杆质量可忽略,拖把头与地板之间的动摩擦因数为常数μ，重力加速度为g.某同学用该拖把在水平地板上拖地时，沿拖杆方向推拖把，拖杆与竖直方向的夹角为θ.

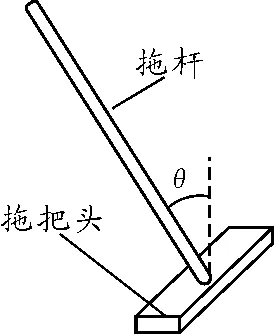
图1

(1)若拖把头在地板上匀速移动，求推拖把的力的大小.

(2)设能使该拖把在地板上从静止刚好开始运动的水平推力与此时地板对拖把的正压力的比值为λ.已知存在一临界角θ0，若θ≤θ0，则不管沿拖杆方向的推力多大，都不可能使拖把从静止开始运动.求这一临界角的正切tanθ0.

解析：(1)设该同学沿拖杆方向用大小为F的力推拖把.将推拖把的力沿竖直和水平方向分解，由平衡条件有

Fcosθ+mg=N

(1)

Fsinθ=f

(2)

式中N和f分别为地板对拖把的正压力和摩擦力.由摩擦定律有

f=μN

(3)

联立式(1)～(3)得

(4)

(2)若不管沿拖杆方向用多大的力都不能使拖把从静止开始运动，应有

Fsinθ≤λN

(5)

这时，式(1)仍满足.联立式(1)、(5)得

(6)

现考察使式(6)成立的θ角的取值范围.注意到式(6)右边总是大于零，且当F无限大时极限为零，有

sinθ-λcosθ≤0

(7)

使式(7)成立的θ角满足θ≤θ0，这里θ0是题中所定义的临界角，即当θ≤θ0时，不管沿拖杆方向用多大的力都推不动拖把.临界角的正切为tanθ0=λ.

学生丢分的原因有：

(1)部分学生不清楚这是一个静力学平衡问题；

(2)绝大多数学生能列出式(5)、(6)，却想不到F可以取无穷大的极限；

(3)题中定义的临界角θ0的物理意义不清晰.

针对上述问题，笔者从摩擦角概念来分析本题的几何意义，可以使以上问题迎刃而解.

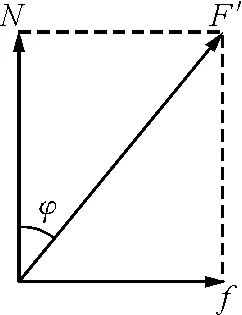
图2

设某物体在另一个物体表面运动时，受到的正压力为N，摩擦力为f，其合力为F′，它们的矢量关系如图2所示.则有

把φ称为滑动摩擦角.由于最大静摩擦力通常认为等于滑动摩擦力，所以，最大静摩擦角等于滑动摩擦角，简称摩擦角.当N和F′夹角小于摩擦角φ时，则f为静摩擦力，物体间保持相对静止.

在滑动摩擦条件下，由于μ为定值，故φ一定为定值.在保持相对滑动条件下，当外界条件变化时，引起N,f变化，但只会引起F′的大小变化，不会改变合力F′的方向.

图3

置于水平面上的物体质量为m，物体与水平面间的动摩擦因数为μ，现用一与竖直方向成θ角的斜向下的力F推物体，如图3所示，φ为摩擦角，当θ≤φ时，无论推力F多大物体仍处于静止状态，这是一种自锁现象.因此，本题第(2)问是一个自锁问题.

由摩擦角的观点解释这一自锁现象，将物体所受的支持力N和摩擦力f合成一个力F′，可以等效认为物体受G，F，F′三个力作用.很明显，当θ≤φ时，不管推力F多大，物体不可能获得水平方向的加速度，这时,物体间的摩擦力总为静摩擦力，保持相对静止，物体将始终处于静止状态，即产生自锁现象.当θ>φ时，只要推力F足够大，物体可以获得水平方向的加速度，使物体运动起来.

由上述分析可知，题中定义的临界角θ0实际上就是摩擦角，所以，有

tanθ0=λ

摩擦角除了可灵活解决静力学平衡的难点问题，还可以在摩擦力做功、弯道技术、破冰船船体设计等方面得到应用，限于篇幅，本文不再赘述.

参考文献

1 程稼夫.中学奥林匹克竞赛物理教程.力学篇.摩擦角及应用.北京：中学科学技术出版社，2010.264