特高压直流输电塔风振响应参与模态分析

段松涛， 吴海洋， 包永忠， 舒爱强

(1.电力规划设计总院， 北京 100120; 2.中南电力设计院， 湖北 武汉 430071)

输电塔具有轻质、高柔、小阻尼的特点，被视为典型的风敏感性结构。基于准定常理论，对格构式塔架顺风向风振响应的计算方法已有较为充分的研究[1～5]。《架空送电线路杆塔结构设计技术规定》[6]中采用杆塔风荷载调整系数来考虑脉动风的动力作用，也就是通常所说的风振系数，并且规定当塔高超过60 m时，按照GB 50009-2001《建筑结构荷载规范》[7]采用分段风振系数，然而输电塔在横担处质量和外形均有突变，并且一阶振型并非线性，故《建筑结构荷载规范》所给风振系数计算表达式并不适用于输电塔这种特殊结构。文献[8]按照《建筑结构荷载规范》类似的方法，基于随机振动理论推导了适用于一阶振型为主的输电塔风振系数计算方法。值得注意的是，无论是《建筑结构荷载规范》中给出的高层建筑或高耸结构风振系数计算方法，还是文献[8]中给出的输电塔风振系数计算方法，都是假定结构振动能量主要集中在一阶振型，故其风振系数计算公式可通过一阶振动恢复力计算得到，通常的输电塔都满足该条件，故可按照此方法计算其风振系数。然而，随着电压等级的不断提高，输电塔横担长度逐渐增加，特别是±800 kV特高压直流输电塔的横担长度有的已超过20 m。随着输电塔横担长度的增加，其扭转频率逐渐降低，风振计算时扭转耦合效应不容忽视。本文将运用随机振动和结构动力学方法，基于准定常理论，考虑扭转耦合效应，计算±800 kV特高压直流输电塔风振响应，分析输电塔风振响应与参与计算模态的关系，并对特高压直流输电塔风荷载作用下的构件设计提出建议。

1 脉动风荷载谱的确定

根据准稳定假定，由顺风向紊流谱直接得到顺风向脉动风荷载谱(不考虑气动导纳的影响)。通常，风速谱采用Davenport谱，其表达式为[9,10]

(1)

格构式塔架在高度z处单位高度上的风荷载可由下式表示：

(2)

式中：ρ为空气密度；CD为阻力系数；B(z)为z高度处的截面宽度；R(z)为z高度处单位高度实际面积与轮廓面积的比值。

(3)

(4)

z高度处荷载谱密度函数为：

(5)

式中：Sv(n)为z高度处风速谱，可以采用Davenport谱。参考文献[9],脉动风荷载可以分解为：

Pd(z,t)=wf(x)f(t)

(6)

式中：wf(x)为表述空间位置的确定性函数；f(t)为表述脉动风随机性的随机函数。因此脉动风荷载谱可表达为：

(7)

(8)

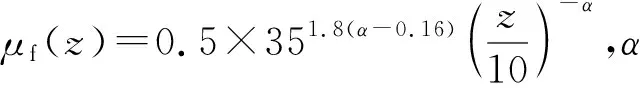
2 相干函数的确定

强风观测表明，各点风速、风向并不是完全同步的，甚至可能是完全无关的，因此表述脉动风需要考虑空间相关性，包括侧向左右相关和竖向上下相关，将输电塔架划分为若干段，各段的风荷载谱相干函数为[10]：

(9)

3 风振响应计算

根据随机振动理论，输电塔架第l阶广义脉动风荷载谱密度可以表达为：

R(zi,zj,n)A(zi)A(zj)φl(zi)φl(zj)

(11)

式中：SP(zi,n)、SP(zj,n)分别为i、j段的风压谱密度；A(zi)、A(zj)分别为i、j段的挡风面积；φl(zi)、φl(zj)分别i、j段的l阶振型响应系数。将(8)式和(9)式代入(11)式可得到：

(12)

因此，考虑前m阶振型的输电塔风振响应可由下式计算得到：

σR(zi)=

(13)

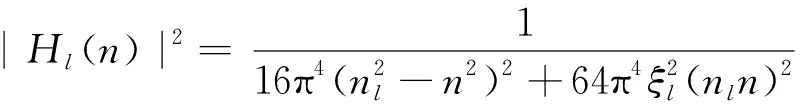
4 工程实例

某±800 kV特高压直流输电塔架全高63.5 m，50年一遇大风10 m高度处平均风速为28 m/s。按照上述方法步骤，编制程序，计算该输电塔架在来流风速垂直于线路方向时该方向的风振系数。本文采用有限元计算该输电塔的自振频率。如图1所示为该输电塔架的前4阶振型，第5振型频率为4.96 Hz。我国规范[7]规定，基频大于 4 Hz 的结构可不考虑脉动风压引起的结构振动，故第5阶及以上的振型贡献可不考虑。

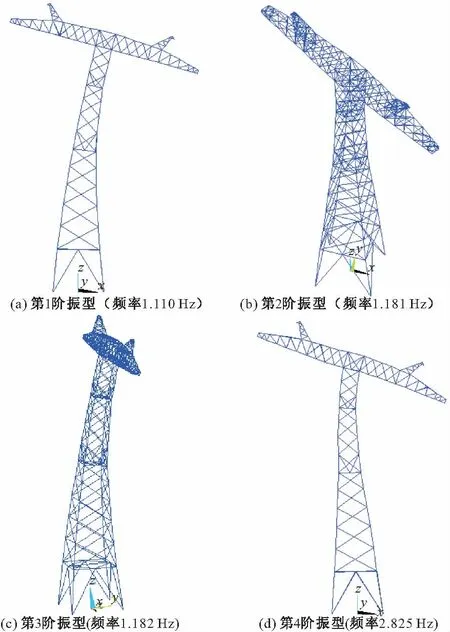
图1 振型

从图1可见，该特高压直流输电塔的第1阶振型表现为垂直于线路方向的平动，第2阶振型表现为扭转振动，第3阶振型表现为顺线路方向的平动，第4阶振型表现为垂直于线路方向的高阶平动，由于垂直于线路方向与顺线路方向的平动振型独立不相关，而垂直于线路方向与扭转向的振型是耦合的，故当计算垂直于线路方向的风振响应时只需考虑第1阶、第3阶和第4阶振型，即垂直于线路方向的1、2阶平动和扭转振型。按照荷载规范，取峰值因子μ=2.2，计算得到输电塔位移风振响应如图2所示，图中z表示各段重心高度，H表示输电塔总高度，曲线最高点为横担部分，紧接着自上往下为塔身顶部到塔腿的各塔身分段。通过比较图2(a)和(b)可见，当仅考虑第1阶平动振型时，横担位移风振响应与塔身顶部相同，当同时考虑第1阶平动振型和扭转振型时，横担位移风振响应将增大47%，可见扭转振型对横担位移风振响应的贡献不可忽略。通过比较图2(b)和(c)可以发现，两条曲线基本相同，说明第2阶平动振型贡献非常小，计算输电塔风振响应时仅需考虑第1阶平动和扭转振型。

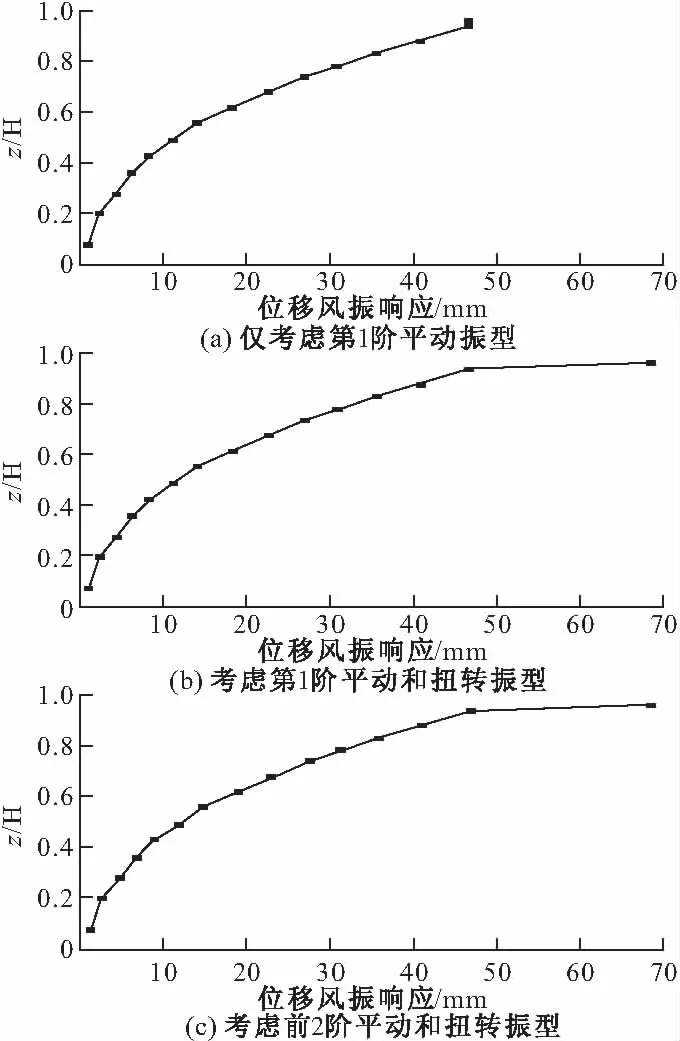
图2 位移风振响应沿高度变化

为了更加直观地表现各阶振型对输电塔风振响应的贡献，将塔顶位移风振响应和横担位移风振响应随计算模态数量的变化表示如图3所示，图中纵坐标表示考虑不同模态数计算得到的位移风振响应，横坐标模态数1表示仅考虑第1阶平动振型，模态数2表示同时考虑第1阶平动和扭转振型，模态数3表示同时考虑前2阶平动和扭转振型。从图3可见，随着计算模态数的增加，位移风振响应逐渐增大并趋于稳定，其中，对于塔身顶部位移风振响应，当考虑第1阶平动振型时即已趋于稳定，而对于横担位移风振响应，当考虑第1阶平动振型和扭转振型时才趋于稳定。因此，计算类似特高压直流输电塔风振响应时，仅考虑一阶平动振型是不够的，扭转振型不容忽略，否则计算结果偏小，偏差接近50%，这种情况下，仅考虑一阶振型的风振系数计算方法将使结果偏于危险。

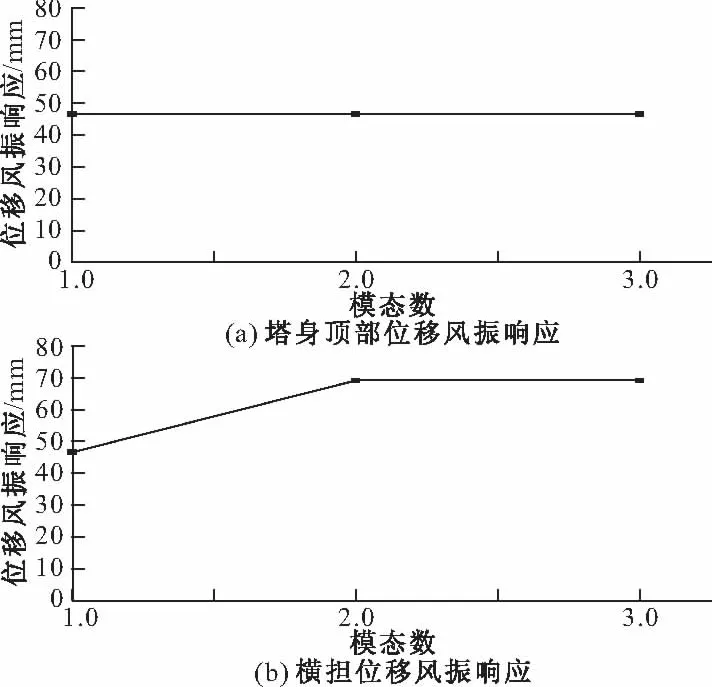
图3 风振响应随计算模态数的变化

传统的高层建筑和高耸结构的风振系数都是根据一阶振型的振动恢复力计算得到，当结构振动以一阶振型为主时，将一阶振动恢复力作为等效静力风荷载，并据此计算风振系数的方法是完全可行的，然而当结构风振响应计算需要考虑多阶振型贡献时(比如特高压直流输电塔)，就无法确定采用哪一阶振型的振动恢复力作为等效风荷载，此时通过理论方法计算得到准确的内力风振系数是不可能的，只能得到准确的位移风振系数，然而输电塔设计往往都是以构件内力作为主要控制条件，位移一般都不控制。因此，由于特高压直流输电塔的扭转振型对风振响应的贡献较大，仅考虑一阶振型是不够的，从而导致其风振系数的计算非常困难，目前还没有准确的理论方法。

目前输电线路杆塔的结构设计都是通过对荷载进行组合，然后按照组合荷载计算构件内力，最后根据构件内力进行构件设计。我国《建筑结构荷载规范》所指的荷载组合实际是指荷载效应组合，一般情况下对于线性结构，荷载组合与荷载效应组合是等效的，对于非线性结构，两种组合就会产生不同的结果，此时应该严格按照荷载规范的规定进行荷载效应组合。本文建议由目前铁塔设计采用的荷载组合改为荷载效应组合，原因主要有两点：(1)随着结构计算的不断精细化，考虑塔线耦合可能成为趋势，而塔线耦合体系为非线性结构体系，此结构体系构件设计必须采用荷载效应组合；(2)前文已经阐述过，随着横担长度的增加，扭转振型贡献逐渐增大，此时风振系数的计算非常困难，尤其是无法得到准确的内力风振系数，但是风振响应，即风荷载作用下的构件内力是可以通过随机振动理论计算能得到的，此内力即构件的动力风荷载效应，因此，如果采用荷载效应组合，就可以避免求风振系数，为输电塔风荷载工况下的构件计算开辟一条新的、简便且直接的途径。

5 结 论

随着特高压输电塔的横担长度逐渐增加，扭转振动频率逐渐降低，接近于第1阶平动频率，导致扭转模态贡献显著，故扭转模态不容忽略，否则将导致位移风振响应结果偏小近50%。根据计算结果，对特高压直流输电塔风荷载作用下的构件设计提出如下建议：(1)特高压直流输电杆塔的风振响应计算必须考虑扭转振型的贡献，否则结果偏小；(2)建议铁塔设计由目前采用的荷载组合改为荷载效应组合，从而可以避免陷入计算风振系数的困境。

[1] Holmes J D. Along-wind responses of lattice tower: Part I─Derivation of expressions for gust response factors [J]. Engineering Structures, 1994，16(4): 287-292.

[2] Holmes J D. Along-wind response of lattice towers—II. Aerodynamic damping and deflections[J]. Engineering Structures, 1996, 18(7): 483-488.

[3] Holmes J D. Along wind response of lattice towers—III. Effective load distributions[J]. Engineering Structures, 1996, 18(7): 489-494.

[4] Juhásová E. Quasi-static versus dynamic space wind response of slender structures[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69: 757-766.

[5] Yasui H, Marukawa H , Momomura Y, et al. Analytic study on wind-induced vibration of power transmission towers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(1): 431-441.

[6] DL/T 5154-2002，架空送电线路杆塔结构设计技术规定 [S].

[7] GB 50009-2001，建筑结构荷载规范 [S].

[8] 吴海洋, 王开明, 冯云巍. 基于准稳定理论输电塔风振系数计算方法[J]. 电力建设，2009,30(6):36-38.

[9] Davenport A G. The spectrum of horizontal gustiness near the ground in high winds [J]. Quarterly Journal of the Royal Meteorological Society, 1961, 87(372): 194-211.

[10] 张相庭, 结构风压和风振计算[M]. 上海:同济大学出版社, 1985.