大体积混凝土温度应力场变化分析

谭广柱， 刘书贤， 张 弛,3， 麻凤海

(1．辽宁工程技术大学 产业开发处， 辽宁 阜新 123000；2．辽宁工程技术大学 土木工程学院， 辽宁 阜新 123000；3．本溪钢铁集团建设有限责任公司， 辽宁 本溪 117000；4．大连大学 建筑工程学院， 辽宁 大连 116622；)

大体积混凝土的温度裂缝主要是由水泥水化热造成的，为了提高大体积混凝土结构的施工质量，必须控制大体积混凝土施工和养护过程中由于水泥水化放热所产生的温度变化和温度应力。由于大体积混凝土结构体系自身的复杂性和所处环境的多样性，大体积混凝土的开裂问题必须考虑其养护过程中温度应力的影响[1～11]。

对于大体积混凝土温度应力场的研究分析，美国主要是利用有限元时间过程的分析方法，日本则主要是利用约束系数矩阵法；在法国和英国ABAQUS、ANSYS等有限元分析软件则应用比较广泛。美国的威尔逊教授[2]是最早利用有限元时间过程分析法来分析混凝土温度场的；日本的专家学者[3～4]不仅考虑了混凝土徐变应力场的计算，而且对温度应力场也进行了深入研究；我国朱伯芳院士[5～6]编制了我国第一个用于计算混凝土温度徐变应力的有限元程序，并将其应用于三门峡重力坝温度应力分析中；刘光廷[7]等将断裂力学的研究成果融入功能强大的仿真程序中，应用“人工短缝”成功地解决了溪柄碾压混凝土薄拱坝两岸的温度拉应力问题。

为了更进一步的分析研究在养护过程中大体积混凝土裂缝控制方法，本文基于大体积混凝土四维温度场与温度应力场理论，通过现场实测，利用有限元模拟分析具体工程的大体积混凝土四维温度场，分析数值模拟结果与现场实测结果的温度场变化趋势及吻合度，以验证数值模拟结果的可靠性和准确性，为大体积混凝土工程施工方案制定提供理论依据。

1 大体积混凝土四维温度场理论

1.1 基本概念

“四维温度场”理论是指在三维空间(x,y,z)的基础上考虑时间一维t的温度场，此时为不稳定的三维瞬态温度场：

T=T(x,y,z,t)

(1)

等温面是指在某一时刻，温度场内具有相同的温度值各点所构成的一个曲面；温度梯度是指在温度场内的某点的最大升温速率的单位矢量，可表示为：

(2)

根据热传导定律，热流密度和温度梯度之间的函数关系可表示为：

(3)

(4)

式中，λ为导热系数，kJ/(m·h·℃)。

1.2 数学模型

考虑到现场施工中的大体积混凝土工程的实际边界条件的影响因素较多，需要依据实际工程的详细情况来确定边界条件。基于四维温度场理论的大体积混凝土的数学力学模型为：

(5)

本文需要对某综合楼大体积混凝土基础的温度场在空间域和时间域中的实际分布进行分析研究，参考文献[5～10]“四维温度场”理论中的实际计算模型的相关知识，建立该大体积混凝土基础四维温度场的理论计算模型如下：

(6)

1.3 控制大体积混凝土温度裂缝的方法

大体积混凝土的温度裂缝在施工养护过程中分为升温过程和降温过程：

大体积混凝土处于升温阶段时：

(7)

大体积混凝土处于降温阶段：

(8)

定义温度应力：

σ(t)=σw(t)+σN(t)

(9)

其中：σw(t)为外界约束条件下，大体积混凝土整体变形所产生的应力，σw(t)的产生主要是由于在外界约束存在的条件下，大体积混凝土结构内部由水化放热所导致的最高温度Tmax降至周围环境温度Th(t)产生的收缩应力所引起的；σN(t)为内部约束条件下，大体积混凝土表面质点与内部质点所产生的应力，应力σN(t)是在内部约束条件下，由大体积混凝土结构的中心与其表面温度之差 ΔT(t)产生的变形不协调所产生的。

温度差值ΔT为：

ΔT(t)=[Tj+T(t)-Ts(t)-Td(t)]max

-Th(t)|t=t0

(10)

式中，t0为大体积混凝土结构内部温度降至环周围境温度时的时间；Td(t)为大体积混凝土非收缩应力所产生的收缩当量温度；Th(t)为大体积混凝土结构所处的环境温度值；

要控制大体积混凝土结构的温度裂缝，需要满足以下条件：

Rf(t)>σN(t)+σz(t)+σs(t)+σ0(t)

-σX(t)

(11)

其中，Rf(t)为大体积混凝土结构在养护过程处于t龄期时的抗拉强度；σz(t)为外界约束条件下，大体积混凝土结构降温产生的应力；σ0(t)为其它环境因素约束所产生的应力；σX(t)为混凝土结构由于徐变所产生的应力。

2 工程实例

2.1 工程概况及计算模型

某圆形基础，外部直径35 m，内部直径10 m，厚度4 m，属于典型的大体积混凝土，板面标高为-5.7 m，板底标高为-7.7 m，设置二条后浇式膨胀加强带，后浇式膨胀加强带宽度为2 m，将底板分成三块。底板后浇式膨胀加强带以外混凝土为补偿收缩混凝土，强度等级为C30，抗渗等级P6；后浇式膨胀加强带混凝土强度等级为C35，抗渗等级为P6，并掺加膨胀剂，在地下室外墙浇筑前完成，分析模型如图1所示。

图1 有限元分析模型

在有限元分析计算过程中，考虑到能量守恒原理，需要利用数值分析软件ANSYS热分析来完成，选取具有三个方向的热传导能力Solid70三维热实体单元，它可以实现匀速热流的传递[11～13]。该筏板基础大体积混凝土的热力学性能以及物理力学性能参数如表1。

表1 计算参数

2.2 现场测试数据分析

为了保证数值分析的可靠性、准确性和对比性，首先对工程施工中大体积混凝土的温度变化和应力场变形进行分析。

为了保证测量方案具有较好的代表性，准确掌握大体积混凝土结构的温度场变化过程，将该基础分为上、中、下三组多个温度测试点，以保证能够同时准确测试不同深度部位的混凝土内部温度变化过程；具体布置见图2。

图2 测温点布置

通过现场监测获得的大体积混凝土各个部位的温度变化曲线如图3～8所示。

图3 养护过程中基础A处的温度变化

图4 养护过程中基础B处的温度变化

图5 养护过程中基础C处的温度变化

图6 养护过程中基础A处的温度应力变化

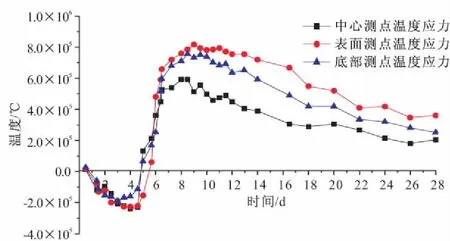
图7 养护过程中基础B处的温度应力变化

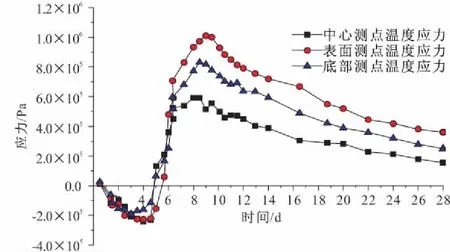
图8 养护过程中基础C处的温度应力变化

通过分析大体积混凝土基础的温度变化曲线和温度应力变化可以看出：在养护的过程中，随着大体积混凝土水泥水化热反应的结束及混凝土热量的不断散失，大体积混凝土基础逐渐完成了由升温阶段向降温阶段的过渡。

浇筑初期大体积混凝土的温度是呈线性变化上升的，随着养护时间的不断增加，大体积混凝土基础的中心部分温度迅速增加，并且温度峰值出现在厚度相对较大的部位。在短时间内，大体积混凝土温度增加了40℃，此时由于结构边界条件的约束，在不利组合条件下将可能超过混凝土的抗拉强度而导致温度裂缝的出现。基于此，在工程现场进行施工时，应该对大体积混凝土的温度场和现场气象状况进行连续的实时监测，采取适合于当地实际情况的养生方式，在养护期间需要根据天气的变化状况，定期对混凝土结构洒水，保证混凝土内部相对湿度的基本稳定。

2.3 大体积混凝土温度场有限元数值分析

为了能够显示大体积混凝土在养护过程中，其温度应力场的分布变化过程，利用有限元分析软件ANSYS对其养护过程进行分析，如图9所示。

图9 混凝土温度随龄期变化

图10 基础外环混凝土温度随龄期变化

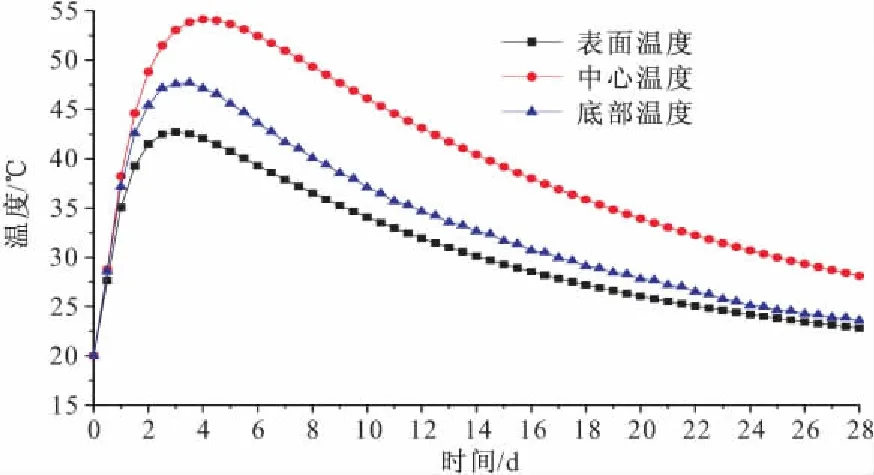
图11 基础中环混凝土温度随龄期变化

图12 基础内环混凝土温度随龄期变化

通过分析图10～12可知，在整个养护的过程中，大体积混凝土的放热升温过程一般是在3～4天内基本完成，浇筑养护的过程中期温度变化的升温速率一般可以达到0.4 ℃/h左右；当温度达到峰值后一般能够维持18 h左右，之后的养护过程中，大体积混凝土开始进入温度下降状态，一般持续18天左右，之后的温度场的分布比较均匀，降温基本趋于稳定。在后期养护过程中，高温集中区始终存在于大体积混凝土基础的内部，降温速度比较缓慢的也同样出现在厚度相对较大的部位。养护实际到达20天以后，大体积混凝土的温度场基本上是均匀分布的，并且逐渐趋于稳定。

从空间角度分析发现由于大体积混凝土水化热效应的显著性导致其应力分布呈现出不均匀性的特点，这主要是由于大体积混凝土不同部位与周围环境进行热交换的差异所引起的，基础中央上表面与环境的空气发生热交换，热量散失较好，故其温度曲线明显低于中心和底部温度曲线；而基础中央的下表面和中心由于与外界接触的面积较小，加之边界约束条件的限制，发生热交换不够充分，故而温度较高。

通过对比数值分析结果与现场监测的数据可知：大体积混凝土的温度变化曲线虽然发展变化趋势吻合较好，但是数值分析的曲线明显比现场测试的数据曲线要光滑，这主要是由于在有限元分析中未考虑施工工艺、养护条件的偶然性变化以及弹性模量、边界条件、热力学公式等参数的选择过于理想化，导致数值分析与现场实测曲线不一样，说明ANSYS模拟分析大体积混凝土温度场变化趋势是基本可行的，但是仍存在一定的误差。

3 结 论

由于水泥的水化作用，在浇筑初期产生大量的水化热，无论升温阶段，还是降温阶段，混凝土的中心温度总是高于混凝土表面温度，膨胀速率要比表面混凝土的膨胀速率大。混凝土其峰值温差最大值为26℃，基本上能够满足《大体积混凝土施工规范》规定的峰值温度不得高于30℃的规定。应该对大体积混凝土温度场和现场气象状况进行连续的实时监测，采取适合于当地实际情况的养护方式，根据天气的变化状况，定期对混凝土结构洒水，保证混凝土内部相对湿度的基本稳定。如果养护不当，则出现温度裂缝的可能性较大。通过数值模拟可以有效地预先判断工程中可能出现的技术难点和受荷载的薄弱环节，提前做好裂缝控制工作，为今后同类大体积混凝土施工方案制定提供理论依据。

[1] 朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社，1999.

[2] Malkawl Abdallah I Husein,Mutasher Saad A,Qiu Tony J.Thermal-structural modeling and temperature control of roller compacted concrete gravity dam[J]. Journal of Performance of Constructed Facilities, 2003, 17(4): 177-187.

[3] Kawaguehi Tohru,Nakane Sunao.Investigations on determining thermal stress in massive concrete structures [J]. ACI Materials Journal, 1996, 93(l): 96-101.

[4] Kim Jang-Ho Jay, Jeon Sang-Eun, Kim Jin-Keun. Development of new device for measuring thermal stress[J].Cement and Concrete Research, 2002,32(10): 1651-1654.

[5] 朱伯芳.多层混凝土结构仿真分析的并层算法[J].水力发电学报, 1994, (3):21-30.

[6] 朱伯芳,许 平.混凝土坝仿真计算的并层算法和分区异步长算法[J].水利发电,1996,(1):38-43.

[7] 刘光廷,谢树南,李鹏辉,等. 碾压混凝土拱坝设人工短缝的应力释放及止裂作用[J]. 水利学报, 2002, (6): 9-14.

[8] 李守巨,刘迎曦. 基于模糊理论的混凝土热力学参数识别方法[J]. 岩土力学, 2004, 25 (4):570-573.

[9] GB 50496-2009,大体积混凝土施工规范[S].

[10] 刘文燕,耿耀明. 热工参数对混凝土结构温度场影响研究[J]. 混凝土与水泥制品, 2005, (1):11-15.

[11] 刘 睫, 陈 兵. 大体积混凝土水化热温度场数值模拟[J]. 混凝土与水泥制品, 2010,10(5):15-27.

[12] 周 莹,王双喜. 塑料连栋温室覆盖层的能量平衡模型的理论研究[J]. 中国农学通报, 2010,26(20): 402- 405.

[13] 石亦平，周玉蓉. ABAQUS有限元分析实例详解[M].北京：机械工业出版社,2006.