基于拉索振动监测的车辆荷载识别研究
张福俭, 李 惠
(哈尔滨工业大学 土木工程学院, 黑龙江 哈尔滨 150090)
过去的二三十年间,很多移动荷载识别方法纷纷涌现,例如解释法I[1],解释法II[2],时域法[3],时频域法[4],优化状态估计方法[5]和有限单元法[6]等。通常采用的简化桥梁模型有:(1)无质量梁连接的集中质量模型[1]; (2)简支或连续的欧拉梁模型[2~5, 7~14];(3)有限梁单元[6];(4)简支的正交异性板[15]。
移动荷载识别领域还有很多其他的研究成果在此未能一一列出,但是现有的研究一般都是以梁桥为研究对象。然而,并不是所有类型的桥梁都适用于采用梁模型,比如斜拉桥和悬索桥。因此,对于大跨度的斜拉桥进行动态荷载识别研究就变得非常必要,对于桥梁的设计、运营、维护以及安全评估都具有非常重要的意义。
本文拟对斜拉桥上的荷载识别问题进行研究。拉索是斜拉桥上非常重要的结构构件,新建的很多大跨度斜拉桥上都安装有健康监测系统。本文提出了一种通过斜拉索的振动和风速监测来进行斜拉桥上车辆荷载识别的方法。
1 斜拉索振动理论
将某一根斜拉索隔离出来作为研究对象,其简图如图1。
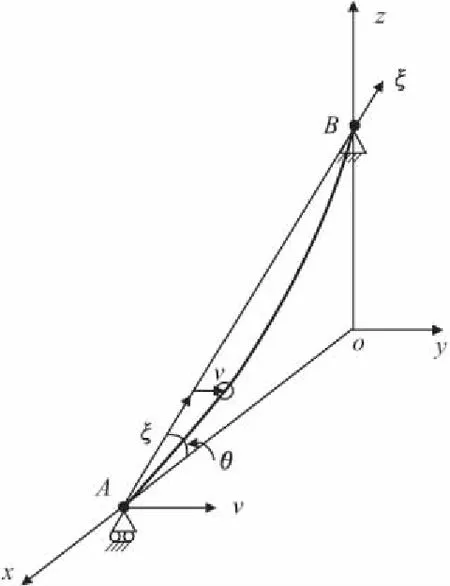
图1 斜拉索振动示意
根据拉索的振动方程[16](忽略索的抗弯刚度、重力以及轴向振动)
(1)
式中,T为索的拉力,m为单位长度质量,c为单位长度阻尼,fw为沿索长的分布外荷载。
对于两端简支索,采用
(2)
其中
(3)
将公式(2)代入公式(1),可得
(4)
然后在公式(4)两端同时乘以φi(ξ),并对ξ从0~L进行积分,有
(5)
代入振型函数公式(3)并考虑正弦函数的正交性,有
(6)
公式(6)可以写成矩阵形式
(7)
其中模态刚度K=[kij]、模态质量M=[mij]、模态力F=[Fq1,Fq2,…,Fqr]T,式中
(8)
(9)
(10)
其中δij为克罗内克函数(Kronecker Delta),其定义如下:
(11)
2 车辆荷载及其参数的识别方法
假设通过桥梁的有限元模型或者现场的实验数据,某一根具体的索的索力影响线是可以得到的,记为函数ψ(·)。对于大跨度的斜拉桥而言,车桥耦合振动的影响比较小,忽略其影响。当ψ(·)函数已知时,由多辆车所引起的索的动刚度可以表示为
(12)
其中τj是第j辆车的上桥时间,1/σj是第j辆车的速度,Vj是第j辆车的重量。
将方程(12)代入方程(7)可得
(13)
定义状态变量
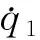
σ1…σr]T
(14)
这样,状态空间内的系统方程可以表示为

(15)
记
(16)
这样

Or×rIr×rOr×3k-M-1(αK0)-M-1C(-M-1K0q)g(1)τg(1)Vg(1)σ︙︙︙g(k)τg(k)Vg(k)σTO3k×rO3k×rO3k×3k
(17)

(18)
(19)
(20)
通过连续系统方程可以得到离散的系统方程为[17]
Zk=Φ(tk+Δt,tk)Zk-1
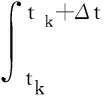
(21)
其中
(22)
(23)
本文中,采用索上的加速度观测进行估计,因此观测方程为
yk=h(Zk)+vk
(24)
这样
(25)
方程(22)和方程(24)适用于采用离散的扩展卡尔曼滤波,这样采用扩展卡尔曼滤波技术,状态变量可以通过局部的加速度观测按如下步骤估计得到。
预测:
(26)
(27)
更新:
(28)
(29)
(30)
(31)
Pk|k=(I-KkHk)Pk|k-1
(32)
其中
(33)
(34)
3 数值实验研究
3.1 研究对象及背景
本文的数值实验基于南京长江三桥。南京三桥位于现南京长江大桥上游约19 km处的大胜关附近,横跨长江两岸,南与南京绕城公路相接,北与宁合高速公路相连,全长约14.89 km,其中跨江大桥长4.744 km,主桥采用主跨648 m的双塔钢箱梁斜拉桥,桥塔采用钢结构,为国内第一座钢塔斜拉桥,也是世界上第一座弧线形钢塔斜拉桥,于2005年10月建成通车(图2)。
本研究中采用ANSYS商用程序建立了斜拉桥的有限元模型,如图3所示。桥塔和主梁采用Beam44单元,斜拉索采用Link10单元。
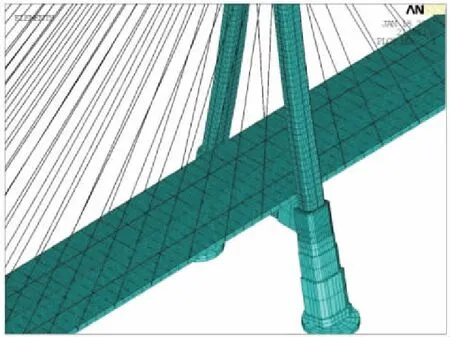
图3 有限元模型局部
通过ANSYS模拟上下游两个行车道内的100 t的重车以20 m/s的速度通过时造成J03索的索力变化,结果如图4所示。

图4 索力时程
3.2 风荷载模拟
本文中采用的索横向荷载为人造风荷载。根据Davenport谱进行风速模拟,10 m米高风速采用10 m/s,得到脉动风压如图5所示,为了激励起比较丰富的频率成分,本文中假设风荷载输入为单点时变激励。

图5 模拟风荷载
将图4中的索力时程和图5中的模拟风荷再代入公式(7),即可进行响应求解。
3.3 车辆的荷载识别
得到模拟的振动响应之后,加入白噪声模拟观测噪声,即可通过公式(26)~(34)进行识别。
3.3.1工况1
已知到达时间和通过速度,识别1辆车的荷载值(图6)。此工况中,已知信息为观测到的一点加速度数据和输入风荷载,并且已知车载的速度和上桥时间。加速度信号加入了30 dB高斯白噪声。

图6 已知时间和速度时一辆车的识别结果
3.3.2工况2
同时识别两辆车的车重(图7)。基本假设和已知同工况1,不同的是待识别车重为两车。第一辆车重为100 t,第二辆车中为80 t。
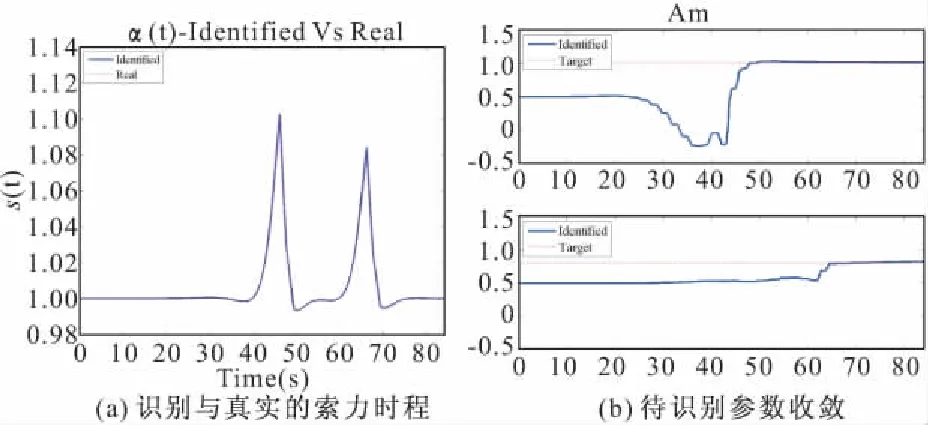
图7 已知时间和速度时两辆车的识别结果
3.3.3工况3
在工况3中,观测信息仍为还有30 dB噪声的索上一点加速度和风荷载。车辆荷载的速度、上桥时间和车重都是未知的。这时采用本文所提出的方法得到的识别结果如图8所示。从图8的结果来看,在车重、车速以及上桥时间都未知时,待识别参数多,识别的效果不如速度、上桥时间已知时只识别车重的结果。
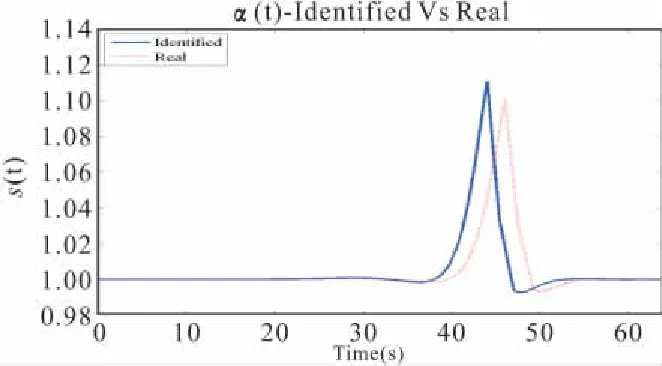
图8 车重、车速和上桥时间均未知识别结果
3.3.4工况4
基本假设同工况3,待识别参数车辆为两辆。一辆为100 t,0 s上桥,另一辆为60 t,20 s上桥。两车车速均为20 m/s。结果如图9所示。
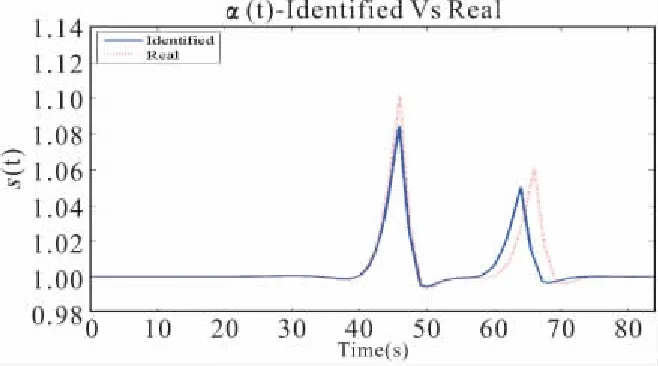
图9 两辆车参数未知时的识别结果
4 结 论
本文提出了一种基于斜拉索的加速度和风荷载监测为基础的斜拉桥上移动荷载识别方法。以南京长江三桥为背景的数值仿真得出结论如下:(1)本文所提出的荷载识别方法用于在车辆的速度、上桥时间已知的前提下识别车辆荷载重量时,具有较高的精度;(2)本文所提出的荷载识别方法可用于识别三项未知参数:车辆的速度、上桥时间以及车重。但其识别精度不及只识别车重的情形;(3)本文所有识别用加速度均含有30 dB的白噪声,表明该方法具有一定的抗噪能力。
[1] O’Connor C, Chan T H T. Dynamic wheel loads from bridge strains [J]. Journal of Structural Engineering, 1988, 114(8): 1703-1723.
[2] Chan T H T, Law S S, Yuang T H, et al. An interpretive method for moving force identification [J]. Journal of Sound and Vibration, 1999, 219(3): 503-524
[3] Law S S, Chan T H T, Zeng QH. Moving force identification: a time domain method [J]. Journal of Sound and Vibration, 1997, 201(1): 1-22.
[4] Yu L, Chan T H T. Moving force identification based on the frequency-time domain method [J]. Journal of Sound and Vibration, 2003, 261(2): 329-349.
[5] Law S S, Fang Y L. Moving force identification: optimal state estimation approach [J]. Journal of Sound and Vibration, 2001, 239(2): 233-254.
[6] Law S S, Bu J Q, Zhu X Q, et al. Vehicle axle loads identification using finite element method [J]. Engineering Structures, 2004, 26(8):1143-1153.
[7] Zhu X Q, Law S S. Moving forces identification on a multi-span continuous bridge [J]. Journal of Sound and Vibration, 1999,228(2): 377-396.
[8] Chan T H T,Yung T H. Theoretical study of force identification using prestressed concrete bridges[J]. Engineering Structures, 2000, 22(11): 1529-1537.
[9] Zhu X Q, Law S S. Dynamic axle and wheel loads identification: laboratory studies [J]. Journal of Sound and Vibration, 2003, 268(5): 855-879.
[10] Zhu X Q,Law S S. Identification of vehicle axle loads from bridge dynamic responses [J]. Journal of Sound and Vibration, 2000, 236(4): 705-724.
[11] Chan T H T, Yu L, Law S S, et al. Moving force identification studies, I: theory [J]. Journal of Sound and Vibration, 2001, 247(1): 59-76.
[12] Chan T H T, Yu L, Law S S, et al. Moving force identification studies, II: comparative studies [J]. Journal of Sound and Vibration, 2001, 247(1):77-95.
[13] Chan T H T, Law S S,Yung T H. Moving force identification using an existing prestressed concrete bridge [J]. Engineering Structures, 2000, 22(10): 1261-1270.
[14] Chan T H T, Yu L, Law S S,et al. Parameter Studies of Moving Force Identification in Laboratory [C]// Chan S L, Teng J G. Advances in Steel Structures. Hong Kong: Elsevier, 1999: 537-544.
[15] Law S S, Bu J Q, Zhu X Q, et al. Moving load identification on a simply supported orthotropic plate [J]. International Journal of Mechanical Sciences, 2007, 49(11): 1262-1275
[16] 欧进萍. 结构振动控制:主动, 半主动和智能控制 [M]. 北京:科学出版社,2003.
[17] Franklin G F, Workman M L, Powell D. Digital Control of Dynamic Systems [M]. Sydney: Addison-Wesley Longman Publishing Co, 1997.

