基于Hedonic模型的轨道交通沿线土地增值研究

聂 琪， 张 瑾， 张新华， 高 柳， 李 彬

(华中科技大学 土木工程与力学学院， 湖北 武汉 430074)

城市轨道交通具有运量大、速度快、节约能源和用地等特点。随着我国城市化进程的加快，城市的交通及环境问题日益严重，城市轨道交通在我国正面临前所未有的发展机遇，目前我国各城市轨道交通建设迅速增长，进入了前所未有的高速发展阶段。随着城市轨道交通的建设，城市道路交通状况得到明显改善，同时城市轨道交通站点也随之成为生活、商务、文化、娱乐等各种设施场所的集中处，给沿线土地带来了显著的增值效益。但是城市轨道交通建设营运资金需求量巨大、盈利困难并且资金回收期长，导致资金约束成了城市轨道交通发展的主要障碍，另外轨道交通沿线的绝大部分土地增值效益也没有得到合理的分配。对城市轨道沿线土地价值进行定量分析，从而研究土地价值的空间分布规律，将有利于土地增值效益的合理分配，为城市轨道交通建设提供融资新途径。

Hedonic模型，目前在国内外已被广泛地应用于房屋住宅价格与土地价值研究。特别是在城市轨道交通对沿线土地增值效应的研究领域上，其作为一种较为新颖的研究思路与研究方法，已得出了大量研究成果。例如清华大学何剑华使用Hedonic模型研究了北京地铁对沿线住宅价格的增值效应[1]，荷兰学者Debrezion (2011)、英国学者Riley(2001)等人研究论证了建成后的城市轨道交通对沿线土地价值显著的增值效应[2,3]。Hedonic模型在评估轨道交通沿线住宅价格和土地价值时，比交通成本模型等其它模型更为准确，考虑因素也比较全面[4]。本文以武汉市轨道交通2号线为例，基于Hedonic模型开展城市轨道交通沿线的土地增值定量分析。

1 模型应用基础

1.1 Hedonic模型的函数形式

Hedonic模型的函数形式一般有基本线性形式、对数形式、对数线性形式与半对数形式4种简单形式[5]。

(1)线性形式(Linear)：

P=α+∑βiXi+ε

(1)

(2)对数形式(Log-Log):

lnP=α+∑βilnXi+ε

(2)

(3)对数线性形式(Log-Linear):

lnP=α+∑βiXi+ε

(3)

(4)半对数形式(Semi-Log)：

P=α+∑βilnXi+ε

(4)

采用Hedonic模型进行城市轨道交通沿线的土地增值定量分析时，选择适当的函数形式对研究结果的正确性十分重要，选择不当的函数形式，得到的结论可能会严重地偏离现实情况。

1.2 Hedonic模型的检验

进行模型方程的具体构建时，首先应对模型变量进行筛选，并测定模型方程的拟合程度、检验回归方程和回归系数的显著性[6]。另外根据模型论证的具体需求，也应进行模型自变量共线性诊断、方差齐性检验及残差正态性检验[7,8]。

(1)拟合优度检验

回归方程的拟合程度通过多重回归判定系数R2测定，R2值范围为0～1，R2越接近1，则模型拟合程度越高，反之，R2越接近0，拟合程度越低。

(2)回归方程的显著性检验(F检验)

回归方程的显著性检验一般采用F检验，利用方差分析的方法进行。如果F值较大，则说明自变量造成的因变量的变动远远大于随机因素对因变量造成的影响。

(3)回归系数的显著性检验(t检验)

回归系数的显著性检验是检验各自变量对因变量的影响是否显著，从而找出哪些自变量对因变量的影响是重要的，哪些是不重要的。

要检验变量对因变量的线性作用是否显著，要使用t检验。如果某个自变量的回归系数的标准误差较大，则必然会得到一个相对较小的t值，表明该自变量解释说明因变量变化的能力较差。因此当某个自变量的t值小到一定程度时，该自变量就不该再保留在回归方程中。

2 模型的具体构建

本文以武汉市轨道交通2号线(金银潭站至光谷广场站)为例，在查阅国内外相关研究的基础上，对武汉市轨道交通沿线的土地增值进行定量分析。基本线性回归方程为Hedonic模型方程形式中较为简单的一种，并且通过对各种函数形式进行试算，比较分析各种函数形式试算结果后，基本线性形式拟合程度通过了检验且拟合程度较高，因此本文采用Hedonic模型中的基本线性回归模型进行分析。

2.1 基本假设

基于Hedonic模型对武汉市轨道交通沿线的土地增值进行定量分析时，有如下2个基本假设[9]：首先，假设用房产价格代替土地价格，其次，进行分析时，只考虑普通住宅的价格。在国内，房地产的概念是指房屋和土地的产权和资产，因此房地产包含土地的产权和资产，并且房屋价格包含了土地价值，因此在本文中用房产价格代替土地价格进行武汉市轨道交通沿线的土地增值定量分析。进行定量分析时，不同住宅类型的考虑因素差别很大，无法全面反映所有的因素，本文只考虑普通住宅的价格。

2.2 基本线性模型与变量的选取及量化

(1)基本线性模型

采用Hedonic模型中的基本线性回归函数模型进行分析，建立的函数模型如下：

P=α+β1x1+β2x2+…+β12x12+ε

ε～N(0,σ2)

(5)

式中：P表示住宅价格，单位万元；x表示特征变量；α表示常数项；ε表示随机误差项；β表示特征变量的系数。

(2)变量的选择及量化

变量的选择对模型构建的准确性有着十分重大的影响。选择变量过少，将无法构建满足一定要求的模型，且误差很大，选择变量过多，则会出现自变量之间的共线性问题。参考国内外研究学者的文献资料并结合武汉市房产市场具体情况，我们最终选取的主要特征变量为12个，其中建筑特征变量5个，邻里特征变量4个，区位特征变量3个[7]。对变量进行归纳与量化后,得到Hedonic模型变量量化表，如表1所示。

表1 Hedonic模型变量

2.3 样本选择与数据收集

本文研究所采用的数据形式主要为新建住宅单元销售价格和二手房交易挂牌价格，数据主要来源于实地调研与房产信息网站。最终获得334个武汉市轨道交通2号线沿线住宅价格样本，涵盖轨道交通2号线21个站点。

3 模型定量分析

3.1 模型构建概述

采用Hedonic模型中的基本线性回归模型进行分析，模型表达式如式(5)所示。

一般来讲，随着距最近轨道交通站点距离的增加，站点周边的土地价格呈现明显的递减趋势，且影响区范围在2000 m左右。但是在最接近轨道交通站点周边500 m左右距离内的土地价格可能造成一定的负面影响，使住宅价格有所下降。

因此，模型构建时需对房产价格数据进行筛选。选取距最近轨道交通站点距离为500～2000 m的房产价格数据，最终实际参与模型构建的数据数为202个。

模型构建借助于SPSS 19.0统计分析软件的回归分析功能，选择“Enter”方法进行回归分析，即12个特征变量全部进入模型参与计算。

3.2 回归检验及相关分析

(1)变量筛选

模型变量显著性可通过t值来检验，若某变量t检验的显著性水平大于10%，则应该将该变量剔除。分析结果显示，装修、车位、教育配置、自然环境、500 m内公交站点数这5个变量的t检验的显著性水平大于10%，因此这5个变量与因变量之间的线性关系没有通过显著性检验，在分析过程中应将之剔除。

(2)拟合优度检验

将剩余7个特征变量采用Enter方法进行回归分析，所有自变量进入模型，并得到模型汇总表(表2)。

表2 模型汇总

表2给出了模型整体拟合效果的概述，模型的拟合优度系数R为0.852，判定系数R2为0.726，因此模型因变量与自变量之间线性关系显著，模型解释能力达到72.6%，可见模型线性方程的拟合优度高。

(3)整体线性显著性检验与方差分析

模型方程的整体线性显著性检验通过模型方差分析中的F检验值进行检验，方差分析结果如表3所示。

表3 方差分析

从表3中可以看出模型方差的显著性F检验值为73.333，显著性水平P的值为0.000<0.05，表明模型方程的特征自变量与因变量之间的线性关系非常显著，模型可以通过检验。

(4)回归系数估计与显著性检验

回归系数表如表4所示。

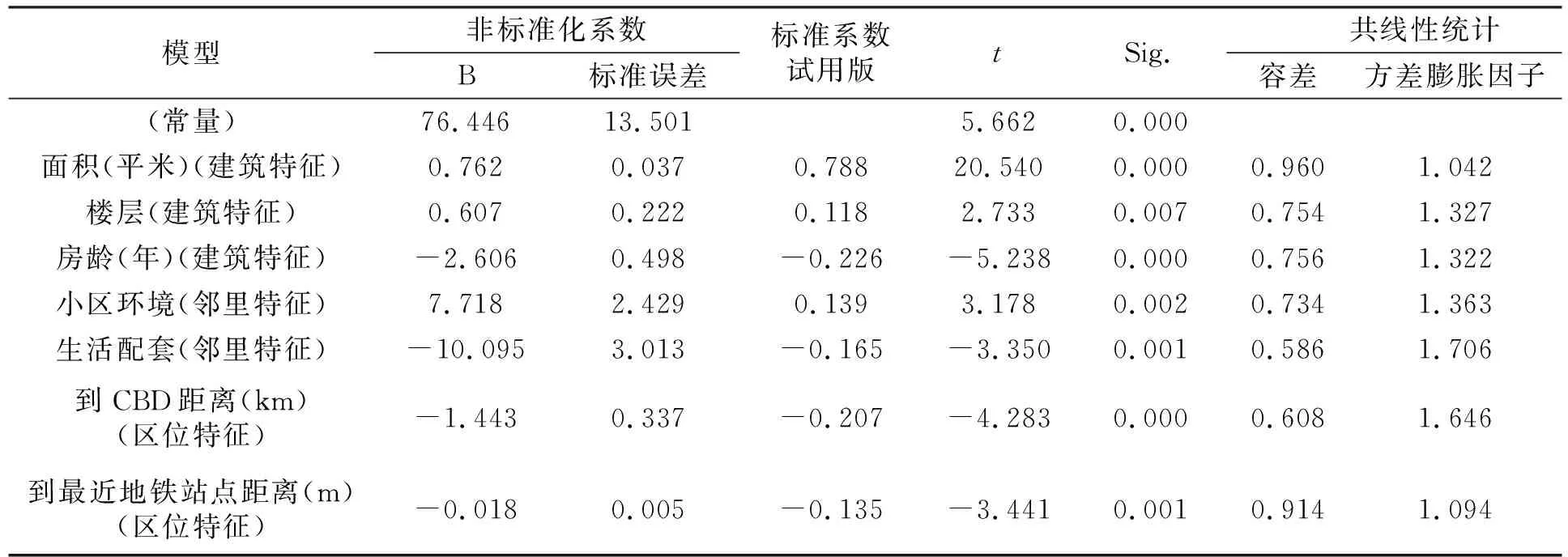
表4 回归系数

从上表中可以看出，剔除5个不显著的变量后，模型各个特征变量的显著性水平均小于0.1，都通过了显著性t检验，更加合理。

(5)自变量共线性诊断

自变量之间的共线性通过Tolerance(容差)与VIF(方差膨胀因子)反映。由表4可知，在剔除不显著自变量后，7个变量的容差值均大于0.1，方差膨胀因子值均远小于10，因此各变量之间均不存在多重共线性的现象。

(6)方差齐性检验与残差正态性检验

方差齐性是指残差的分布是常数，与自变量或因变量无关，即残差应随机分布在穿过零点的水平直线两侧。因变量预测值与残差的散点图如图1所示。

图1 因变量预测值与残差的散点

从图中可以看出绝大部分观测量随机落在水平直线正负2之间，分布比较均匀。

标准化残差正态P-P概率如图2所示，残差分布直方图如图3所示，由图可知残差的分布近似于正态分布。

图2 标准化残差正态P-P概率

图3 残差分布

3.3 模型结论

综合以上所有结论，根据回归系数表(表4)得到模型各变量系数，最终模型的表达式如下(共12变量，排除变量5个，有效变量7个)：

住宅价格P=76.446+0.762x1+0.607x4-2.606x5+7.718x6-10.095x8-1.443x11

-0.018x12

(6)

由模型表达式可知，X12系数为-0.018，表明住宅远离最近轨道交通站点1 m，住宅价格下降0.018万元(180元)。因此可得出结论如下：城市轨道交通对沿线土地价值(房产价格)有显著的增值效应，且随着距离最近轨道交通站点距离的增加，站点周边的土地价格呈现明显的递减趋势。

4 结 论

本文以武汉市轨道交通2号线为例，基于Hedonic模型对轨道交通沿线土地价值进行研究，模型采用基本线性回归形式。模型定量分析中，首先对样本数据与变量进行了筛选，然后对模型进行了全面的回归检验与相关分析，包括拟合优度检验、整体线性显著性检验、方差分析、自变量共线性诊断等。

定量分析的研究成果表明，城市轨道交通对沿线土地价值(房产价格)有显著的增值效应。政府及相关部门必须认识到这部分增值效益的重要性，并规划好城市轨道交通沿线土地的开发方式，从而有利于土地增值效益的合理分配，解决在城市轨道交通建设中出现的资金短缺和运营亏损等问题。

由于研究涉及因素的复杂性，本文尚存在一些不足之处。在定量研究中，考虑的特征变量有限，因此研究结果与实际情况将存在一定的偏差；另外，目前研究主要是针对武汉市轨道交通2号线，其他线路是否也满足这一结论并未进行研究。在今后的研究中，可以扩大样本容量，将不同路线进行比较得出更具有适用性的结论。

[1] 何剑华.用hedonic模型研究北京地铁13号线对住宅价格的效应[D].北京：清华大学,2004.

[2] Ghebreegziabiher Debrezion，Eric Pels，Piet Rietveld. The impact of rail transport on real estate prices: an empirical analysis of the dutch housing market[J]. Urban Studies, 2011, 48(5): 997-1015.

[3] Don Riley. Taken for a Ride: taxpayers, trains, and HM Treasury[R]. UK: Center for Land Policy Studies, 2001.

[4] 郑捷奋.城市轨道交通与周边房地产价值关系研究[D].北京：清华大学，2004.

[5] 王 琳.城市轨道交通对住宅价格的影响研究——基于特征价格模型的定量分析[J].地域研究与开发,2009,4(2)：57-61.

[6] 宋志刚,谢蕾蕾,何旭洪.SPSS实用教程[M].北京：人民邮电出版社,2008.

[7] 张兆良.地铁对沿线住宅价格的影晌研究[D].西安：西安建筑科技大学,2010.

[8] 王 超.轨道交通对沿线房地产项目价格的影响研究——以南京地铁一号线为例[D].南京：东南大学,2008.

[9] 陈有孝,林晓言,刘云辉.城市轨道交通建设对地价影响的评估模型及实证——以北京市轨道交通为例[J].北京交通大学学报(社会科学版), 2005,4(3)：7-13.

[10] 王 霞,朱道林，张鸣明.城市轨道交通对房地产价格的影响—以北京市轻轨13号线为例[J].城市问题，2004,(6)：39-42.

[11] 张小松,胡志晖，叶霞飞.城市轨道交通开发利益影响范围研究[J].同济大学学报(自然科学版)，2005,(8)：1118-1121.

[12] 祖 明.基于特征价格模型的城市住宅土地价格影响因素研究[D].哈尔滨: 哈尔滨工业大学，2008.