概率论与数理统计课教学的探索与实践*

丛玉华，殷 烁

(通化师范学院 数学学院，吉林 通化 134002)

义务教育新课程标准中数学教学内容被分为四个部分：“数与代数”、“空间与图形”、“统计与概率”、“实践与综合应用”[1]．高中的数学教学内容中概率与统计也是一个主要内容．新课程标准的重大改革之一就是将基础数学内容增加了概率统计的内容．认为“现代社会是一个信息化的社会，人们常常要根据所获取的数据，作出合理的决策．因此要在数学课程中学习统计与概率的基本思想和基础知识，它们是公民的必备常识”[2]．

面对学生基础教育阶段十二年的概率统计学习，大学的数学与应用数学专业的概率统计应该如何教学？笔者认为应该突出大学教学的特点，更好的完成大学课堂教学任务．因此在概率统计习题课教学中做了一些探索与尝试．

1 认清大学数学教学与中学数学教学的主要区别

中小学是基础教育，是为造就数以亿计的高素质劳动者，数以万计的专门人才和大批拔尖人材奠定基础的教育．这一时期开设的数学课程是以学生适应日常生活，参加生产劳动和学习物理、化学、技术等其他课程及进一步学习为基础的．

而大学是一种专业教育，是对学生职业技能训练和未来适应社会能力的培养．因此，大学课堂教学肩负三大任务：一是要教会学生自主的获取知识；二是培养学生的创新精神与创新能力；三是要培养学生系统化掌握知识的能力．大学教育最主要的功能是专业教育，即培养学生树立牢固的专业思想，掌握本专业的基本理论和基本技能，为将来进一步深造或从事专业工作做好充分的准备．大学教育虽然是一种综合素质的培养，但这种综合素质的培养必须靠专业来支撑．任何一个专业目标的实现都必须通过一系列既相互联系，又有明确分工的课程来完成．这一系列课程构成一个完整的系统，而每一门课程自身也是一个系统，它们由自成体系又相互联系的章节，相互联系的一系列概念、判断、推理所构成．于是大学的课堂教学就与中小学有了本质的不同．大学教师不论采用什么模式，什么方法进行教学，都必须坚持一条准则，那就是帮助每一个学生建立自己的知识体系．如果教师仅仅是照本宣科的讲一些条条框框，学生背一些概念、公式、做几道习题，那就根本达不到对知识融会贯通，更谈不上将知识转化为能力，灵活的运用知识．而这基本上是当前大学概率统计教学的实际情况．为扭转这种局面，笔者认为教师在课堂教学中必须把深度和广度结合起来，使学生不仅是了解每门课程内在的知识结构，而是能深刻领会课程所揭示的基本原理，逻辑联系和理论依据；不仅要学好每一门课程，而且能把各门课程知识融会贯通和重组，打下牢固的专业基础；不仅能掌握教科书知识，而且能够以此为基础和线索拓展自己的知识领域，并且具有运用这些专业知识解决实际问题的能力[3]．

2 教学中的两个尝试

2.1 通过画概念图培养学生系统化掌握知识的能力

每一章结束或课程结束的习题课上，教师要将所学的相关知识进行系统复习．抓住这一机会，组织学生画概念图，通过画概念图使学生既能将所学知识系统化又能培养学生系统化掌握知识的能力，从而有利于大学概率统计教学根本任务的完成．

所谓概念图是用来组织和表征知识的工具，它通常是将有关某一主题不同分支和不同级别的概念置于方框中，再以各种连线将相关的概念连接，这样就形成了关于该主题的概念网络，以此形象的说明概念的内涵和相互关系[4]．例如，利用概率统计概念图可使学生很好的掌握这两个数学分支的研究对象、研究条件、研究内容和思想方法的不同(见图1)．

图1 概率统计概念

学生很长一段时期的认识主要局限于对具有因果关系的确定性的把握，而对揭示偶然世界规律的随机变量了解的总是很肤浅．教师可以通过下面两个概念图让学生深刻理解与掌握概率统计中这一最重要的概念．

图2 随机变量概念

对于随机变量概念图中的每一个概念还可以画出它的微观概念图，比如“离散型”概念为主题的微观概念图，如图3所示．

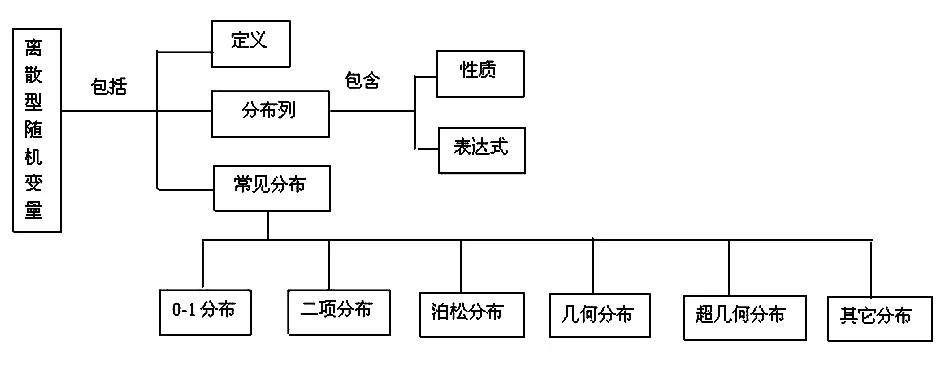
图3 离散随机变量概念图

图4 大数定律概念

在概率统计习题课中经常让学生自己画概念图或自己完善概念图，可以使学生形成系统的知识结构，培养学生的高级思维和创造性思维，提高学生运用概率统计知识分析和解决实际问题的能力．

2.2 习题的选择尽可能联系生活实际

概率统计习题课的任务不仅是要引导学生系统的掌握概率统计的基础知识，还要激发学生学习概率统计的兴趣．培养数学思维能力和提高运用概率统计知识分析和解决实际问题的能力．数学的价值之一是应用价值，它能激起学生的学习欲望.为此，我们在习题课上尽可能的选择一些既能引起学生兴趣又能培养学生解决实际问题能力的习题．如在学习古典概率时，我们选择了抓阄获取一张电影票与顺序无关的实际问题，进而推广到其它抽奖活动与顺序的无关性；学习数学期望和方差时，我们引入了投资风险问题及体育彩票中奖问题；在学习正态分布时，让学生做设计公交车门的高度的实际问题；在学习贝叶斯公式时，我们让学生解决这样的问题：某同学在超市买了一杯酸奶，饮用后出现中毒症状，送医院经抢救脱险，花费医疗费1万元．该同学要求超市赔偿医疗费用，而超市要追究三个厂家的责任．已知超市从三个厂家进货的比例分别为50%，30%，20%，各厂家的次品率分别为2%，4%，5%，由于杯盖上的商标撕掉了，无法辨认是哪个厂家生产的．如果超市想让三个厂家共同支付医疗费用，问三个厂家各支付多少医疗费用才比较合理？这样的问题学生很感兴趣．通过这样的实际问题，学生不仅掌握了一些抽象概念，而且提高了运用概率统计解决实际问题的能力．

在学习数理统计时，可以出一些实际的小问题让学生解决．例如：统计某门课的期末成绩，看其是否符合正态分布，并求出获得优秀、良好等级的概率，进而评价考试的合理性；利用拟合检验考察系别对英语过级率的影响；学习回归分析时让学生记录年级学生的身高及其父母的身高，分析父母身高对子女身高的影响，并预测未来子女的身高，等等．

通过这些改革，学生们的概率统计成绩得到明显提高．所学到的知识不仅更加系统，而且会用这些知识去观察社会，极大的提高了他们解决实际问题的能力．

参考文献：

[1]教育部.全日制义务教育数学课程标准[M].北京:北京师范大学出版社,2001.

[2]教育部.普通高中数学课程标准[M].北京:人民教育出版社,2003.

[3]朱新秤.高等学校教学评估与督导[M].广州:广东高等教育出版社,2009.

[4]刘荣玄.利用概念图促进学生知识建构的探索[J].数学教育学报,2010,19(3):89.

[5]裴新宁.概念图及其在理科教学中的应用[J].全球教育展望,2001(8):47.