基于熵权法的数学课堂评价方法研究

廖纯连，陈华喜

(1.合肥市蜀山区教体局教研室,安徽 合肥 230061；2.合肥市琥珀中学，安徽 合肥 230061；3.蚌埠学院 数学与物理系，安徽 蚌埠 233030)

为贯彻国家基础教育改革的方针政策，本文将采用模糊聚类分析法及主成分分析法在影响数学课堂教学的众多因子中筛选重要指标，构建一套数学课堂教学评价体系，并用基于熵权法对所建立的评价指标体系进行赋权，进而对影响数学课堂教学各因素的重要性进行排序，然后结合模糊综合评判法建立一个数学课堂教学评价模型，并用该模型方法对一堂数学课进行实例分析．以期能为促进学生全面、持续、和谐的发展，推进我国基础教育改革起到一些作用．

1 数学课堂教学评价指标体系的构建

本文根据教育部《义务教育数学学科课程标准》(教基二[2011]9号文)等相关文件精神，结合专家意见以及相关优秀一线教师的教学经验，采用模糊聚类分析法及主成分分析法筛选指标，得到包括教师教学过程、学生学习过程以及教学效果3个一级指标在内，并包含14个二级指标的数学课堂教学评价指标体系，具体如下：

1.1 教师教学过程

教师教学过程包括教学理念、教学策略、教学目标、教学内容、教学过程、教学能力、教学态度以及教学特色8个二级指标．

1.2 学生学习过程

学生学习过程包括学生参与、自主学习以及创新意识3个二级指标.

1.3 教学效果

教学效果包括教学内容完成情况、课堂气氛以及学生知识掌握情况3个二级指标．

2 数学课堂教学评价模型的建立

2.1 评价要素指标体系构建

科学、合理的评价指标体系是对数学课堂教学进行综合评价的基础，也是决定评判结果准确性的前提条件．本文所建立的数学课堂教学评价指标体系如表1所示．

2.2 评语集的设置

根据数学课堂教学评价的实际需要，本文设置的评语集合为“五星”、“四星”、“三星”、“二星”及“一星”五个等级．即评语集合为V={五星，四星，三星，二星，一星}，赋值得V={100,90,80,70,60}.

2.3 用熵权法法确定各级指标权重

设m、n分别表示评价指标与评价对象的个数，X'=(xij')m×n为这m个评价指标和n个评价对象所

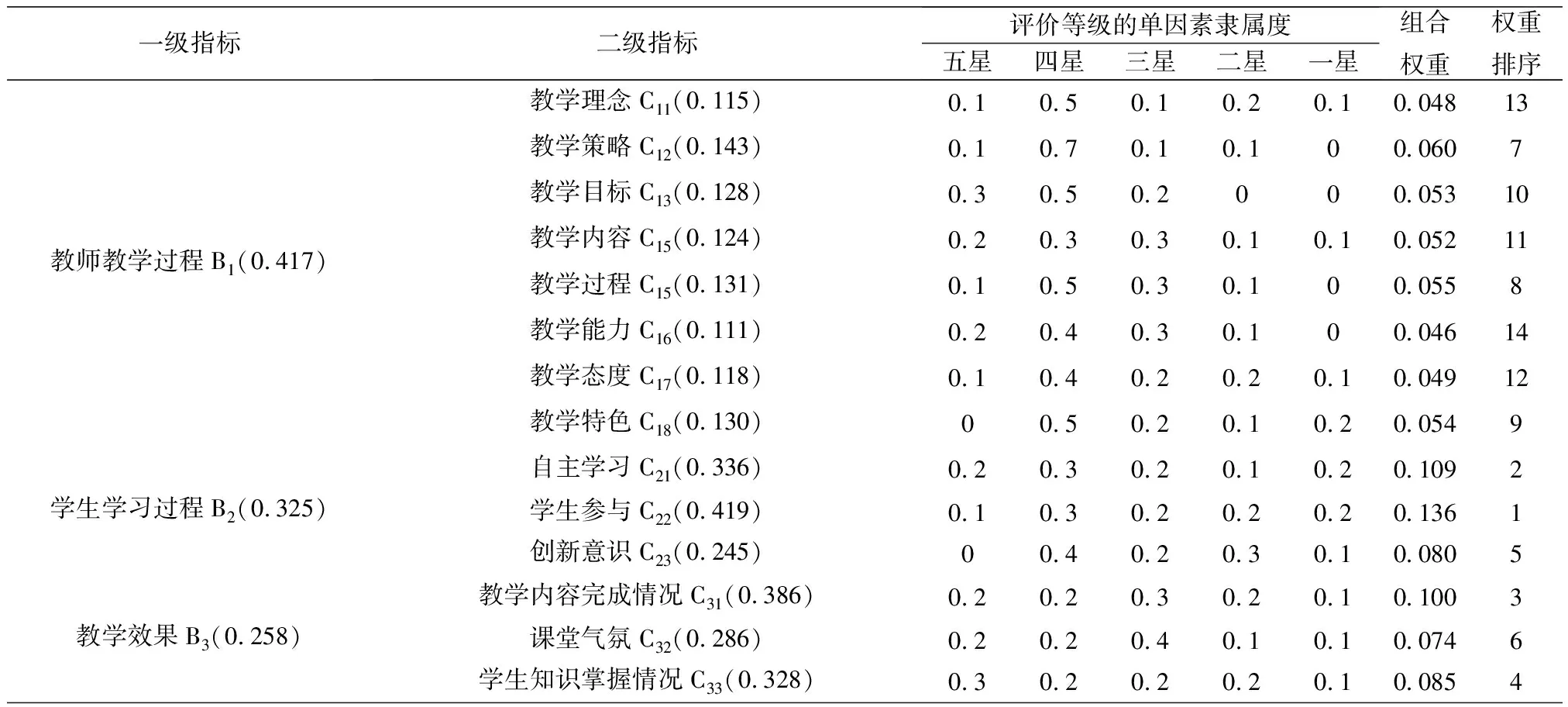
表1 数学课堂教学评价指标体系A

其中，A=(B1,B2,B3)，B1=(C11,C12,C13,C14,C15,C16,C17,C18)，B2=(C21,C22,C23),B3=(C31,C32,C33).

形成的原始数据矩阵，则熵权值的计算步骤如下：

2.4 模糊综合评判的实施

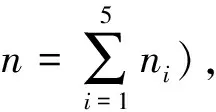
3 数学课堂教学评价的实例分析

下面以合肥市琥珀中学某教师对二次函数内容的课堂教学为例，进行评价．

3.1 各级指标权重的确定

这里仅以一级指标学生学习过程(B2)的3个二级指标——自主学习(C21)、学生参与(C22)、创新意识(C23)为例，说明熵权法确定权重的过程．

对自主学习、学生参与、创新意识3个评价指标，邀请10位相关专家对各级指标的的相对重要程度进行打分，结果见表2．

表2 学生学习过程各子指标的专家评分

(2)根据公式③、④、⑤，求得熵权WB2-C=(0.336,0.419,0.245)，同理，可求得WA-B=(0.417,0.325,0.258)，WB1-C=(0.115,0.143,0.128,0.124,0.131,0.111,0.118,0.130),WB3-C=(0.386,0.286,0.328)，也即表1括号中的各数值；

(3)将一级指标权重与二级指标权重相乘便得到各单因素对该数学课堂教学影响的综合权重，见表1．

3.2 综合评判的实施

3.3 评价得分

3.4 结果分析

根据上述计算可知，该教师数学课堂教学评价结果中有22.4%为“五星”，22.7%为“四星”，22.4%为“三星”，18.5%为“二星”，14.0%为“一星”．根据最大隶属原则，该教师数学课堂教学评价的最终等级应为“四星”级别，综合得分为82.08，课堂教学效果较好，结果与实际情况基本一致；同时，从表1还可以看出：在数学课堂教学评价的一级影响因子中，教师教学过程因素的影响最大，占到41.7%；在二级因子对一级因子的影响中，教学策略(C12)、学生参与(C22)以及教学内容完成情况(C31)对相应一级因子的影响最高，所占比例分别为14.3%、41.9%及38.6%．因此，要提高数学课堂教学水平，应当特别注意这几因素对整体的影响．

参考文献：

[1]徐辉,陈又星.模糊聚类模型及其在国际市场划分中的应用研究[J].地理科学,2010,30(3):350-354.

[2]朱林波.主成分分析法在城市交通可持续发展评价中的应用[J].西华大学学报,2013(1):63-66.

[3]何鑫,朱宏泉,高成凤.基于熵权法与TOPSIS法的房地产项目投资风险评价[J].商业研究,2009(3):105-108.