基于耦合传输线的宽上通带窄带带阻滤波器设计

王占平，杨 博，陈 华，王亚非，王林智，孙 伟

(1. 电子科技大学光电信息学院 成都 610054；2. 领亚电子科技股份有限公司 广东 深圳 518108；3. 东莞岳丰电子科技有限公司 广东 东莞 523590)

微波带阻滤波器广泛应用于现代通信系统和雷达系统中，被用来抑制高功率发射机的杂散谐波、高功率功放的非线性谐波输出以及带通滤波器的寄生通带等。

1 设计原理

1.1 窄带带阻滤波器的设计方法

文献[1]中提出的支线式带阻滤波器应用于窄带带阻滤波器设计时，各支线具有很高的阻抗导致无法实现，但是这种结构的带阻滤波器当相对带宽较大时(如大于40%时)，各支线具有合理的阻抗水平，比较容易实现，因此被用来制作宽带带阻滤波器。为了得到窄带带阻滤波器的实现形式，文献[2]提出了一种基于电容耦合的支线式带阻滤波器结构形式，该形式的带阻滤波器在支线式带阻滤波器结构基础上，通过将λ/4高阻抗支线开路谐振器变换为电容耦合短路并联谐振器获得，其支线阻抗可以任意选择，通常为50 Ω或75 Ω。但这种结构的带阻滤波器具有较差的上通带驻波特性，特别是在阻带中心频率的二倍频率处。为了解决这个问题，文献[3]提出了在支线间的90°连接线中间加入一个集总电容以改善二倍频处的驻波特性。但这样又会影响带阻滤波器阻带的带宽响应，且难以进行滤波器的精确综合设计。文献[4-6]提出了一种对微波窄带带阻滤波器进行精确设计的方法，该方法采用λ/4平行耦合线作为滤波单元节，可获得良好的滤波器响应特性。但这种形式的窄带带阻滤波器在中心频率的三倍频(3f0)处具有寄生阻带，大大限制了它的应用范围。为了解决该寄生阻带问题，文献[7-9]提出了在平行耦合线滤波器节开路端加载集总电容的方法来展宽上通带的范围，但未见深入报道。本文基于该方法进行拓展研究并研制了一个窄带带阻滤波器，获得了较宽的上通带宽带和良好的传输特性。

1.2 窄带带阻滤波器的设计

平行耦合传输线滤波器节如图1所示。

图1 平行耦合传输线滤波器节

其镜像输入阻抗为[10]：

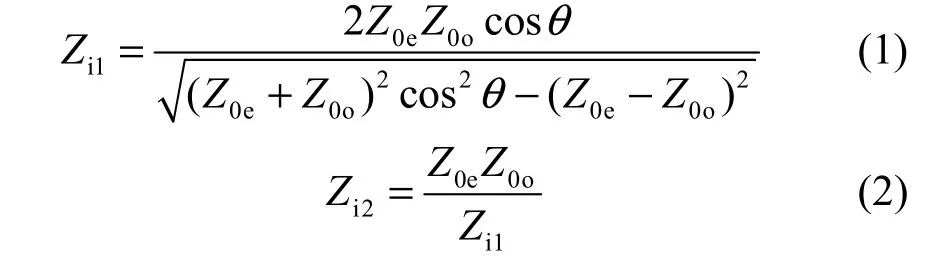
由式(1)可知，这种平行耦合滤波器节具有周期性响应，且周期为π，从而导致基于平行耦合线的带阻滤波器在3f0处具有寄生阻带。为了抑制掉寄生阻带，展宽带阻滤波器上通带的带宽，考虑缩短耦合线的物理长度，在耦合线开路端加载电容Ck进行补偿。加载电容Ck与增加的长度ΔL的关系为[11]：

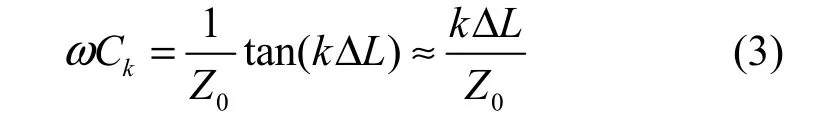
由式(3)可知，终端开路传输线的端电容大小与其等效传输线长度成正比，即端电容越大，其等效的传输线长度越长。利用该结论，通过图1所示的平行耦合传输线开路端加载集总电容就可以缩短平行耦合传输线的物理长度，但是其有效电长度没有发生变化，所以产生的滤波响应没有变化。但是由于带阻滤波器的3f0处的寄生阻带是由λ/4平行耦合线物理结构的周期性响应造成的，原来在3f0处出现的寄生阻带会在更高的频率处产生，因此通过这种在平行耦合线开路端加载适当集总电容的方式能够有效地展宽带阻滤波器上通带的带宽。

本文利用现代网络综合法[12]，采用四阶滤波器方式，得出图2所示的带阻滤波器基型电路。该电路对于窄带带阻滤波器设计并联开路支节的阻抗很高，加工精度难以保证。为此本文采用基于平行耦合滤波节的带阻滤波器设计[5]，通过利用式(4)和式(5)将基型带阻滤波的各节高阻抗谐振器变换成易于加工的平行耦合滤波器节，得到的各节耦合线奇偶模阻抗如表1所示。

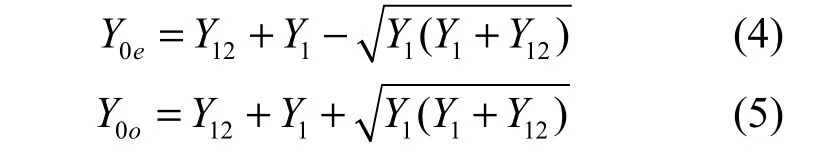
图2 带阻滤波器基型电路

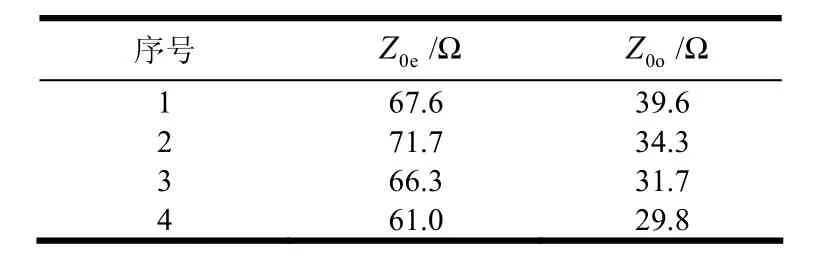
表1 平行耦合滤波节奇偶模阻抗

根据表1所示的奇偶模阻抗，可以得到相应耦合线的物理尺寸。为了尽量缩减该滤波器的物理尺寸，各节耦合线长度选择为60°电长度而不是理论要求的90°，减少的长度通过平行耦合滤波单元开路端加载集总电容来补偿。

2 滤波器仿真

本文设计思路可在Ansoft HFSS中建模进行仿真实现，建立的模型如图3所示。

图3 平行耦合传输线滤波器HFSS模型

该模型的仿真结果如图4所示。

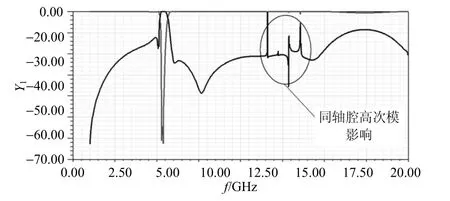
图4 HFSS模型仿真曲线

由图4中可见，通过开路端集总电容的引入，消除了3f0处的寄生阻带，滤波器上通带也具有很好的输入特性，体现了加载集总电容的有效性。另外，图中在频率12.5 GHz左右处出现的一些谐振是由于同轴结构的高次模造成的。根据仿真模型的尺寸，实际制作的滤波器如图5所示。

图5 平行耦合传输线滤波器实物

该滤波器的实测结果如图6所示。

图6 滤波器测试结果

3 结 论

从图6可见：

1) 仿真结果与实测结果的一致性较好，包括在12.5 GHz左右出现的高次模影响。2) 带阻滤波器的中心频率是5.3 GHz，在3f0处即15.9 GHz并没有寄生阻带出现，可见通过在平行耦合滤波节开路端加载集总电容的方法可以很好解决窄带带阻滤波器的3f0寄生阻带问题，延展了上通带的带宽。3) 如果要使带阻滤波器获得更宽的上通带带宽，本文方法有其局限性。因为更宽的上通带带宽意味着要在开路端端面加载更大的集总电容，而大的集总电容在实际结构中很难实现。

[1] MATTHEI G, YOUNG L, JONES E M T. Microwave filters,impedance matching networks and coupling structures[M].New York: Mc Grow Hill, 1964.

[2] YOUNG L, MATTHAEI G L, JONES E M T. Microwave bandstop filters with narrow stopbands[J]. IRE Trans MTT,1962(10): 416-417.

[3] SHAPIR I. An improved narrowband microwave bandstop filter[C]//28th European Microwave Conference Amsterdam.[S.l.]: [s.n.], 1998.

[4] BELL H C. L-resonator bandstop filters[J]. IEEE Trans MTT, 1996, 44(12): 2669-2672.

[5] BELL H C. Narrow bandstop filters[J]. IEEE Trans MTT,1991, 39(9): 2188-2191.

[6] WENZEL R J. Exact design of TEM microwave networks using quarterwave lines[J]. IEEE MTT, 1964, 12(1): 94-111.

[7] SNYDER R V, SHIN S. Parrallel coupled line notch filter with wide spurious-free passbands[M/CD]. [S.l.]: IEEE,2005. IEEE MTT-S Int Microw Symp Dig, 2005, TU4A-3,CD ROM, 45.

[8] LEVY R, SNYDER R V, SHIN S. Bandstop filters with extended upper passbands[J]. IEEE Trans MTT, 2006, 54(6):2503-2515.

[9] GUPTA O P, WENZEL R J. Design tables for a class of optimum microwave bandstop filters[J]. IEEE Trans MTT,1970, 18(7): 402-404.

[10] POZAR D M. Microwave engineering[M]. 3rd ed. New York: John Wiley, 2005.

[11] 清华大学《微带电路》电路编写组. 微带电路[M]. 北京:人民邮电出版社, 1976.Tsinghua University “Microstrip Circuit” Circuit Writing Goup. Microstrip circuit[M]. Beijing: People’s Posts and Telecommunications Press, 1976.

[12] 甘本袚, 吴万春. 现代微波滤波器的结构与设计[M]. 北京: 科学出版社, 1973.GAN Ben-fu, WU Wan-chun. The structure and design of microwave filters[M]. Beijing: Science Press, 1973.