气垫车能耗建模与化简＊（二）

许 烁，罗 哲

（1.上海大学机电工程与自动化学院，上海200072；2.上海交通大学机械与动力工程学院，上海200240

2.3 驱动系统能耗模型

驱动系统能耗Nps作用于轮毂电机，其目的是克服行驶阻力，但也不可避免地伴随有履带打滑耗能和电机线圈铜损。本小节分别从车辆纵向力模型和电机模型的角度推导运行参数之间的关系，建立驱动系统能耗模型。

2.3.1 车辆纵向力模型

气垫车所受纵向力主要包括履带和万向轮的土壤压实阻力 Frc，t和Frc，w、推土阻力 Frb，t和Frb，w、围裙接地阻力Frs、风阻Fra、履带内部阻力Frin，t以及履带驱动力Ft，t。在稳态纵向驱动工况下，这些力的合力为零。下面分别对它们进行建模。

根据图4中的车辆垂向力和力矩的平衡关系，可求履带和万向轮的垂向接地压力Fz，t和Fz，w同气垫压力Fc的关系。代入式（4），可进一步求得Fz，t和Fz，w同载荷分配比δ的关系。

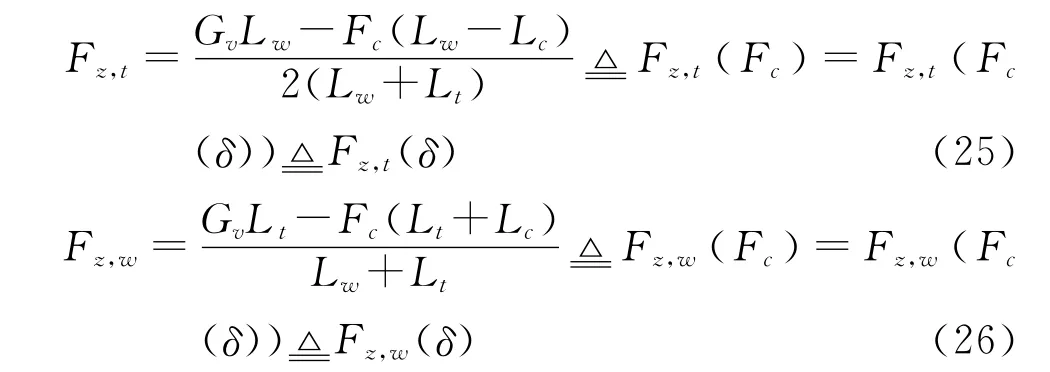
式中，Lw、Lc、Lt均为力矩，Gv为总车重。

图4 整车垂向受力Fig.4 The vertical forces of the vehicle

根据Bekker土壤力模型［1，7］，履带沉陷量ht和万向轮沉陷量hw可通过与Fz，t和Fz，w的关系化简为δ的函数。进一步可求得履带和万向轮的土壤压实阻力 Frc，t、Frc，w和推土阻力Frb，t、Frb，w：

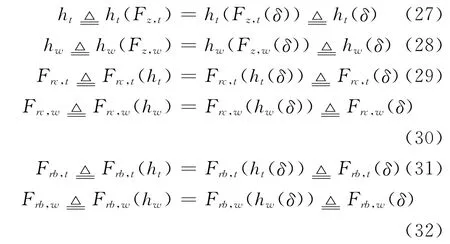
围裙接地阻力Frs同气垫压力Fc的关系如式（33）所示，显然，Frs也可由δ表示：

式中，Gb为车身重量，Csk为围裙阻力系数。

风阻Fra和履带内部阻力Frin，t均与车速u有关。暂且将u视为独立变量，则Fra和Frin，t可表示为

式中，CD为风阻系数，?a为空气密度，Ap，b为车身沿前进方向垂向的投影面积，cin1、cin2为履带内部阻力系数。

履带驱动力Ft，t的定义式如式（36）所示。根据式（25），Ft，t也可简化为关于δ 和滑转率sr，t的表达式：

式中，c、φ、K为土壤参数，At为履带接地面积。

将式（29）～（36）代入车辆纵向力平衡关系式（37），解此方程可得式（38）中车速u同载荷分配比δ和滑转率sr，t的关系。

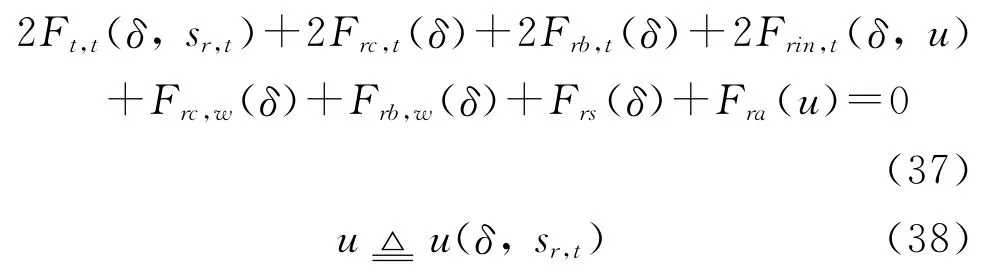
滑转率sr，t能够用来表示履带旋转角速度ωt与车速u的定量关系，反之，ωt可由sr，t和u计算，并进一步化简为δ和sr，t的函数：

2.3.2 电机模型

驱动电机输出转矩和转速同履带输入转矩和转速的相等关系构成连接电机和履带机构的纽带。

在车辆稳态运动的前提下，可由履带驱动力Ft，t求驱动转矩Tt，即电机输出转矩Tm：

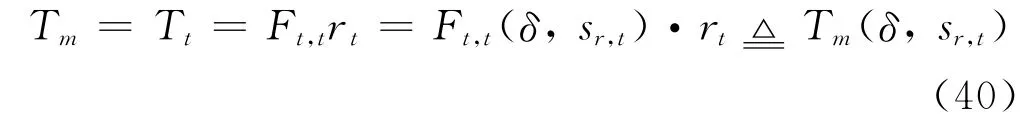
电枢电流Ia与Tm正相关，表达式为

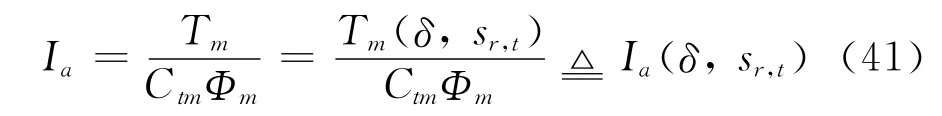
式中，若电机表现出硬特性，则将励磁磁通Φm设为定值；若电机表现出软特性，则Φm与Ia成正比。上述区别不会影响Ia的简化表达式形式。转矩常数Ctm由电机结构决定。

励磁电动势Ea与电机转速nm正相关，nm可换算为电机旋转角速度ωm，若忽略电机与履带之间的相对滑动，ωm又等于履带旋转角速度ωt，由此可建立Ea与ωt的关系，并可根据式（39）进一步化简：

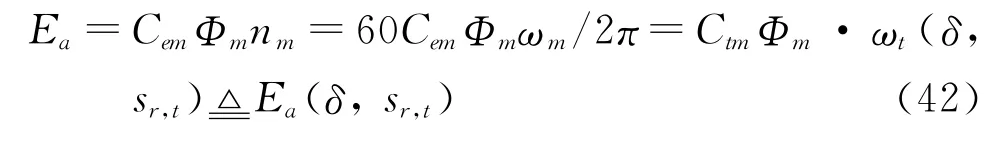
式中，电动势常数Cem由电机结构决定。Ctm与Cem的关系为Ctm＝60Cem/2π。

设导体电阻为Rm，电机给定电压为Um。电机内的电压分配关系如式（43）所示，显然，Um也是δ和sr，t的函数。

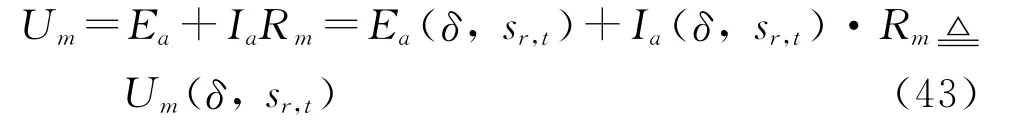
最后，联立式（2）、（38）、（41）和（43），建立驱动系统能耗Nps模型：

2.4 围裙飞高、弹簧变形量和行走机构沉陷量之间的约束关系

将式（38）代入式（24），垫升系统能耗Nls模型中依然包括δ、sr，t、hc等3个自变量。本小节将利用围裙飞高、弹簧变形量和行走机构沉陷量之间的约束关系，建立hc同δ和sr，t的关系，从而进一步化简Nls表达式。

首先求履带悬架的弹簧变形量Δzst。根据式（45）中的履带垂向力平衡关系，悬架弹簧力Fs，t、履带重力Gt和垂向接地力Fz，t的合力为0。联立式（45）和（25），可由式（46）求Fs，t，进一步由式（47）求弹簧变形量Δzst。Δzst为稳态时的弹簧变形量，以压缩为正，拉伸为负。

式中，kst为履带悬架的弹性系数。

文献［8］从气垫车结构的角度，提出了履带处的围裙飞高hct、弹簧变形量Δzst和沉陷量ht三者之间的约束方程：

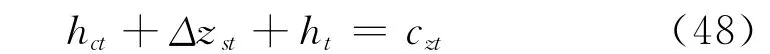
式中，czt为履带处的车辆垂向结构参数。

联立式（27）、（47）和（48），可求履带处的围裙飞高hct：

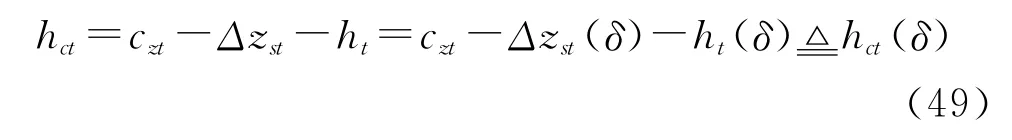
同理，根据万向轮处的垂向结构参数czw可求其悬架弹簧变形量Δzsw（δ）和围裙飞高hcw（δ）。合理地假设垫升力受力点Oc位于气垫中心，则根据图5所示梯形关系，可由hct和hcw求围裙平均飞高hc。

图5 围裙飞高关系Fig.5 The relationship of clearance heights

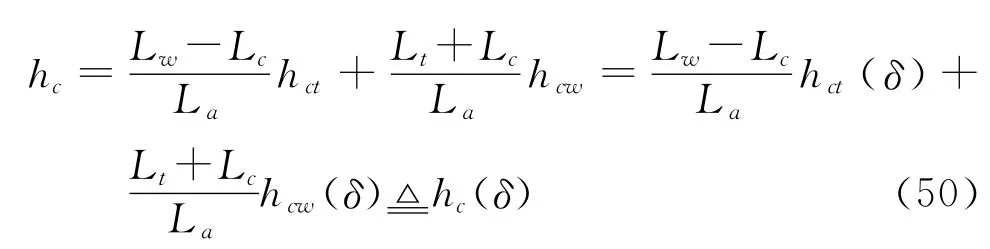
2.5 总能耗模型

将式（38）、（50）代入式（24），可得垫升系统能耗Nls关于δ和sr，t的函数：

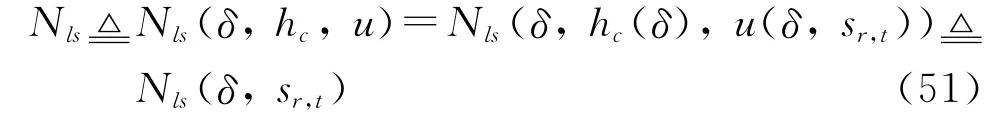
联立式（44）和式（51），可得由独立变量δ和sr，t表示的气垫车总能耗Nv：

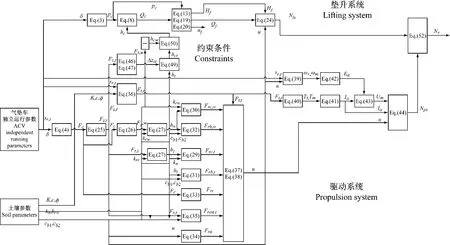
图6 气垫车运行参数及总能耗的求解线路Fig.6 The solving process of vehicle dependent running parameters and energy consumption

气垫车运行参数及总能耗的求解线路如图6所示。

3 结 论

本文将滑转率和载荷分配比作为独立参数，针对稳态纵向驱动工况，建立了车辆运行参数和能耗的求解线路，最终将总能耗表示为这两个独立参数的函数。这说明，理论上存在某种滑转率和载荷分配比组合使气垫车总能耗最小。但是，由于求解线路的复杂性，例如式（19）、（20）构成的代数环以及多个非线性方程的存在，导致Nv的表达式极为复杂，甚至难以写出通式，从而无法用基于偏导数的确定性算法寻优，包括偏导数等于0的解析法、牛顿法和梯度下降法等。因此，下一步的工作为设计启发式算法进行能耗优化。

［1］ Wong，J.Y.Theory of Ground Vehicles［M］.3rd ed.New York：John Wiley ＆Sons，Inc.2001.

［2］ 陈秉聪，王昕.半履带式气垫车最佳功率匹配的研究［J］.青岛大学学报（工程技术版）.1999，14（2）：1－3＋8.

［3］ Luo，Z.，Yu，F.Load distribution control system design for a semi－track air－cushion vehicle［J］.Journal of Terramechanics.2007，44（4）：319－325.

［4］ 许烁，罗哲，喻凡，周科，张勇超.基于总功耗最小的半履带气垫车滑转率控制仿真 ［J］.系统仿真学报.2008，20（16）：4244－4247＋4251.

［5］ Xie，D.，Luo，Z.，Yu，F.The computing of the optimal power consumption for semi－track air－cushion vehicle using hybrid generalized extremal optimization ［J］.Applied Mathematical Modelling.2009，33（6）：2831－2844.

［6］ 龙天渝，蔡增基.流体力学泵与风机 ［M］.北京：中国建筑工业出版社.1999.

［7］ Bekker，M.G.Theory of Land Locomotion ［M］.Ann Arbor：University of Michigan Press.1956.

［8］ 张跃革.半履带式气垫车结构设计及节能机理的研究［D］.长春：吉林工业大学.