黏滞型阻尼器对太阳翼展开性能的影响分析

濮海玲 王晛 杨巧龙

（北京空间飞行器总体设计部，北京 100094）

1 引言

目前，航天器上广泛应用的展开式太阳翼由连接架和数块太阳电池板铰接而成。发射时，它们依靠压紧机构收拢于航天器本体上，发射上天后，压紧机构释放，铰链内预紧的展开弹簧驱动太阳翼展开，联动装置使各部分展开基本同步，展开到位后由铰链的锁定机构将太阳翼锁定为规定刚度的平面。当太阳翼展开到位时，铰链上的锁定机构工作，使太阳翼的运动突然停止，从而使与之直接相连的部件——太阳电池阵驱动机构（Solar Array Drive Assembly，SADA）受到一定的冲击，引起的载荷（主要是弯矩）是太阳翼和SADA 设计的重要指标［1］。

为保证在轨展开锁定的可靠性，太阳翼设计规范要求从收拢到完全展开的整个行程内，在最恶劣环境下的静力矩裕度必须大于1；但这意味着太阳翼展开到位时有较多剩余能量，其中，部分转化为冲击载荷，当冲击载荷超过SADA 的许用值时就会造成损伤。因此，为了保护SADA，须要降低力矩裕度。这两方面的要求构成矛盾。当太阳翼面积大、板数多时，尤为突出。另外，在地面展开试验时，太阳翼面积越大、越重，空气阻力、展开试验设备的摩擦阻力也就越大。当展开试验设备的改进受限时，为了保证展开试验的可靠性，需要更大的驱动力矩，从而使得太阳翼在轨展开锁定时的冲击载荷更大。

在太阳翼上安装黏滞型阻尼器是解决这一矛盾的有效方法，它可以在太阳翼展开过程中耗散系统的机械能量，降低展开速度，从而在不影响展开可靠性的情况下，降低冲击载荷。

由于空气阻力、展开试验设备的摩擦阻力等因素影响，难以在地面试验中完全模拟太阳翼的在轨展开锁定过程，所以一般通过仿真分析来预估锁定产生的冲击载荷。本文利用ADAMS 和Nastran／Patran软件，联合建立了太阳翼在轨展开及地面展开的两种仿真模型，对比分析了无阻尼器以及不同阻尼系数的阻尼器对太阳翼展开动力学性能的影响。

2 典型太阳翼组成

典型太阳翼的组成如图1所示，由连接架、3块太阳电池板和相应的展开铰链等组成，黏滞型阻尼器串联安装在根部铰链上。它是利用黏性液体阻尼材料的黏滞耗能作用，将太阳翼展开到位时的剩余动能耗散掉，以达到减缓冲击的目的。这类阻尼器在国外托佩克斯-海神卫星（TOPEX／Poseidon）等航天器的太阳翼上得到应用［2-3］。

黏滞型阻尼器作为一种耗能装置，不改变太阳翼的刚度，属于速度相关型阻尼器，阻尼力矩T 与连接架的转动角速度v 之间正相关，即阻尼力矩T＝cvm，其中c为阻尼系数，m 为介于0.3～1.0的常数。黏滞型阻尼器的动力性能稳定且耗能能力强，只要有微小的振动就可以耗能，相对于其它类型的阻尼器，具有构造简单、可靠性高等优点［4］。

图1 太阳翼组成与阻尼器安装位置示意图Fig.1 Solar wing configuration and viscous damper assembly position

太阳翼安装黏滞型阻尼器后，在展开初始阶段，由于速度为零，而阻尼器的启动力矩很小，所以对静力矩裕度影响极小。随着太阳翼展开过程的展开速度增加，阻尼器产生较大的阻尼力矩，吸收了大量的能量，限制展开速度的进一步增加，进而降低了锁定冲击；因此，黏滞型阻尼器可以使太阳翼展开静力矩裕度基本不变化，有效降低锁定冲击力矩。

3 阻尼系数对在轨展开的影响分析

以某卫星太阳翼为例，现分析黏滞型阻尼器的阻尼系数对太阳翼在轨展开的影响。假设阻尼力矩与连接架展开角速度近似成正比（m＝1），比较无阻尼器（可视阻尼系数为0）及阻尼系数为60N·m·s／rad和337N·m·s／rad三种情况下的展开情况。

首先，利用Nastran／Patran软件计算各太阳板基频，并将所有正交化的非零Craig-Bampton模态导入ADAMS软件。其次，利用力矩函数模拟铰链摩擦阻力、电缆阻力、绳索联动装置影响等，得到太阳翼在轨展开模型［5-7］。

仿真得到在轨展开时，无阻尼器及阻尼系数分别为60N·m·s／rad和337N·m·s／rad的太阳翼动力学结果。其中连接架角速度-时间曲线如图2所示，展开锁定过程的铰链角度-时间曲线如图3～图5（角度以展开锁定位置为零点），太阳翼根部载荷时间历程如图6、7所示。

由图2可知，无阻尼器时太阳翼连接架展开末速 度 为47 （°）／s，增 加 阻 尼 器 使 阻 尼 系 数 为60N·m·s／rad后，连接架展开末速度降为35（°）／s，随着阻尼系数增加为337N·m·s／rad后，连接架展开末速度进一步降到8（°）／s。

图3 无阻尼器在轨展开角度-时间曲线Fig.3 Curve of deploy angle-time without damper in orbit

图4 阻尼系数为60N·m·s／rad的在轨展开角度-时间曲线Fig.4 Curve of deploy angle-time with damping rate 60N·m·s／rad in orbit

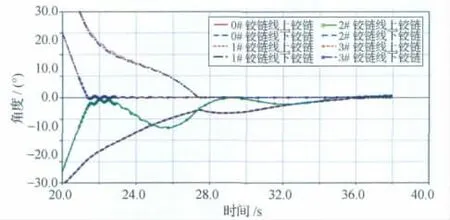
图5 阻尼系数为337N·m·s／rad的在轨展开角度-时间曲线Fig.5 Curve of deploy angle-time with damping rate 337N·m·s／rad in orbit

图6 在轨展开根部铰链力矩时间历程Fig.6 Curve of yoke hinge impact torque time in orbit

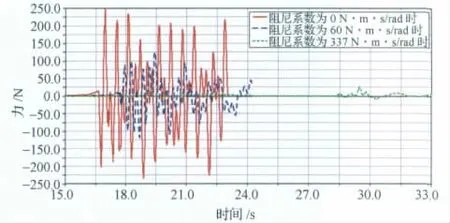
图7 在轨展开根部铰链剪力时间历程Fig.7 Curve of yoke hinge impact shear force time in orbit

对比图3～5，无阻尼器时太阳翼展开时间为16.7s，各铰链锁定同步性较好，各铰链锁定时间差约为0.2s。增加阻尼系数为60N·m·s／rad的阻尼器后，展开时间增加到17.7s，各铰链基本保持同步锁定，但锁定先后顺序变化，根部铰链最后锁定，各铰链锁定时间差约为0.4s。当阻尼系数增加为337N·m·s／rad后，展开时间增加至21.4s，锁定同步性较差，虽然最后各铰链依然能锁定，但各铰链锁定时间差异达到14.4s。

如图6、7所示，当无阻尼器、阻尼器阻尼系数为60N·m·s／rad及阻尼系数为337 N·m·s／rad时，太阳翼根部铰链冲击力矩最大值分别为236N·m，184N·m，62N·m，剪力最大值分别为260N，126N，10N，太阳翼展开锁定冲击力与力矩均随着阻尼器阻尼系数增加而明显下降。

可见，随着阻尼系数的增加，太阳翼在轨展开最大速度降低，太阳翼展开所需时间增大，展开锁定冲击载荷降低，同时，各铰链展开锁定同步性变差；但由于太阳翼在轨展开有足够静力矩裕度的保证，太阳翼最终能够顺利锁定。

4 阻尼系数对地面试验展开的影响分析

在在轨展开模型上添加展开试验设备的吊挂装置，施加外力模拟空气阻力和吊挂装置的摩擦阻力，增加重力环境等，计入吊挂装置的质量，但不考虑吊挂装置的变形，得到太阳翼地面试验展开模型［7-8］。

仿真得到地面试验展开时，无阻尼器及阻尼器取两种阻尼系数情况下的太阳翼动力学结果如下。其中连接架角速度-时间曲线如图8，展开锁定过程的铰链角度-时间曲线如图9～11（角度以展开锁定位置为零点）。太阳翼根部载荷时间历程如图12、13所示。

图8 地面试验连接架角速度-时间曲线Fig.8 Curve of yoke deploy angular velocity-time on ground

由图8可知，无阻尼器时地面试验展开末速度为29（°）／s，阻尼系数为60N·m·s／rad时展开末速度为19 （°）／s，阻 尼 系 数 增 加 为337 N·m·s／rad后展开末速度进一步降到3（°）／s。

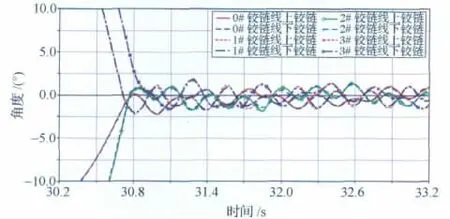
图9 无阻尼器地面试验角度-时间曲线Fig.9 Curve of deploy angle-time without damper on ground

对比图9～11，无阻尼器时太阳翼展开时间为30.7s，各铰链锁定同步性较好，各铰链锁定时间差异约为0.2s。增加阻尼系数为60N·m·s／rad的阻尼器后，展开时间增加到33.2s，各铰链锁定同步性较差，锁定先后顺序发生变化，根部铰链最后锁定，各铰链锁定时间差为6.6s。当阻尼系数增加为337N·m·s／rad后，展开时间增加至47.7s，根部铰链已无法完全锁定，铰链终了平衡位置距锁定位置1.7°。

图10 阻尼系数为60N·m·s／rad的地面试验角度-时间曲线Fig.10 Curve of deploy angle-time with damping rate 60N·m·s／rad on ground

图11 阻尼系数为337N·m·s／rad的地面试验角度-时间曲线Fig.11 Curve of deploy angle-time with damping rate 337N·m·s／rad on ground

图12 地面试验根部铰链矩载荷时间历程Fig.12 Curve of yoke hinge impact torque time on ground

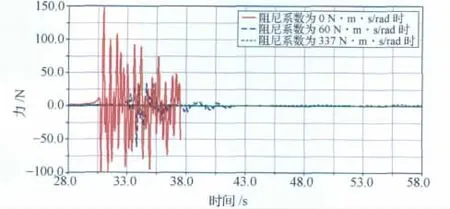
图13 地面试验根部铰链剪力载荷时间历程Fig.13 Curve of yoke hinge impact shear force time on ground

由图12、13可知，无阻尼器时太阳翼地面展开根部铰链锁定冲击力矩最大值为189N·m，剪力值最大值为150N。当阻尼器阻尼系数为60N·m·s／rad时，最大冲击力矩和最大冲击剪力分别为28N·m，62N。当阻尼器阻尼系数增加到337N·m·s／rad时，根部铰链已不能达到锁定位置，将停止在展开力矩与所受阻力矩（主要由吊挂装置的摩擦阻力引起）的平衡位置。

5 地面与在轨展开仿真结果对比

本文计算结果见表1。

表1 阻尼系数对展开性能的影响分析结果Table 1 Analysis result of damping rate vs.deploy performance

由仿真分析结果可知，随着阻尼器的阻尼系数增加，太阳翼在轨展开锁定时间延长，锁定同步性变差，但是依靠根部铰链的驱动力矩能够最终正常锁定。

在地面展开试验时，由于存在空气阻力和展开试验设备吊挂装置摩擦力的影响，使得太阳翼地面展开速度降低，展开同步性变差，完全锁定的耗时增加。相比于无阻尼器展开，有阻尼器且阻尼系数较小时，太阳翼锁定时间明显增长，但尚能完全锁定；当阻尼系数较大时，太阳翼展开速度急剧降低，展开同步性很差，最终太阳翼在未完全锁定的状态达到力矩平衡，根部铰链未能锁定，在地面展开试验时，表现为展开试验故障。此时，须改进太阳翼的地面展开试验方法，以降低或部分抵消地面展开试验设备的摩擦阻力影响，例如，使用气浮装置以减小吊挂装置的摩擦力，或者部分补偿吊挂装置的摩擦力。

综上所述，选择阻尼器的阻尼系数时，除了满足SADA 的许用冲击载荷指标外，还须考虑在轨展开锁定的可靠性，同时应兼顾地面展开试验的难度，在这两者之间权衡，选择适当的阻尼系数值。

6 结束语

太阳翼加装黏滞型阻尼器后，能够减小其展开终了时的角速度，从而显著降低在轨展开锁定时对SADA 的冲击载荷，有效地解决了太阳翼在轨展开可靠所需的较大展开力矩与为保护SADA 须要减小锁定冲击载荷之间存在的矛盾。当太阳翼增加了黏滞型阻尼器后，随着阻尼系数增加，太阳翼在轨展开速度逐步降低，展开锁定冲击载荷降低，同时展开同步性变差。由于有静力矩裕度的保证，依据铰链势能锁定的原则，太阳翼在轨能够顺利锁定。但当阻尼系数太大时，可能会导致地面展开试验时太阳翼锁定不到位、对中度差的现象。此时，须改进太阳翼的地面展开试验方法和展开试验设备，以降低或部分抵消地面因素的影响，或者从地面可试验性的角度出发，折衷选择适当阻尼系数的黏滞型阻尼器，既能满足在轨冲击载荷的要求，又能保证地面展开的可靠性。本文的研究成果，可以为航天器太阳翼合理选用黏滞型阻尼器提供借鉴。

（References）

［1］陈烈民.航天器结构与机构［M］.北京：中国科学技术出版社，2005 Chen Liemin.Spacecraft structure and mechanism［M］.Beijing：China Science and Technology Press，2005（in Chinese）

［2］Maly J R，Pendleton S C，Salmanoff J，et al.Hubble space telescope solar array damper［C］／／SPIE 6th International Symposium on Smart Structures and Materials.Bellingham：SPIE，1999：261-276

［3］Rittweger A，Albus J，Hornung E，et al.Passived damping devices for aerospace structures［J］.Acta Astronautica，2002，50（10）：597-608

［4］Koller F，Nitschko T，Labruyere G.Viscous rotary damper［C］／／Proc.Fifth European Space Mechanisms and Tribology Symposium.Paris：ESA，1993

［5］陈天智，濮海玲，刘立平，等.太阳翼展开锁定过程仿真与试验［C］／／中国宇航学会结构强度与环境工程专业委员会、中国航天第八专业信息网技术信息交流会.北京：中国航天科技集团公司，2007 Chen Tianzhi，Pu Hailing，Liu Liping，et al.Simulation and test of solar array deployment and locking［C］／／Communication Conference by Committee of Structure Strength and Environment Engineering，China Society of Astronautics and the Eighth Specialty Information Web.Beijing：CASC，2007（in Chinese）

［6］陈烈民.太阳翼联动装置绳索的张力变化分析［J］.航天器工程，1999，8（4）：9-13 Chen Liemin.Tension changing analysis for synchronizing mechanism assembly of solar array［J］.Spacecraft Engineering，1999，8（4）：9-13（in Chinese）

［7］Wie B，Furumoto N，Banejee A K.Modeling and simu-lation of spacecraft solar array deployment［J］.Journal of Guidance，Control and Dynamics，1986，9（5）：593-598

［8］王晛，陈天智，柴洪友.太阳翼地面展开锁定的动力学仿真分析［J］.航天器工程，2011，20（3）：86-92 Wang Xian，Chen Tianzhi，Chai Hongyou.Dynamics simulation analysis of solar array ground deployment and locking［J］.Spacecraft Engineering，2011，20（3）：86-92（in Chinese）

［9］Wallrapp O，Wiedemann S.Simulation of deployment of a flexible solar array［J］.Multibody System Dynamics，2002，7：101-125